
- •1. Случайный эксперимент. Пространство исходов. Случайное событие.
- •2. Классическое определение вероятности. Свойства вероятности (из определения). Недостатки определения.
- •3. Основные формулы комбинаторики.
- •4. Геометрическое определение вероятности. Его недостатки. Задача Бюффона. Задача о встрече.
- •5. Частота события. Статистическое определение вероятности. Понятие устойчивости и законе больших чисел. Недостатки определения.
- •6. Алгебра событий. Аксиоматическое определение вероятности. Свойства вероятности из аксиоматического определения.
- •8. Условные вероятности. Теорема умножения вероятности, независимые события. Попарная независимость и независимость в совокупности.
- •9. Вероятность наступления хотя бы одного события.
- •10. Формула полной вероятности. Формула Байеса.
- •11. Схема Бернулли. Формула Бернулли.
- •12. Приближенные формулы для формулы Бернулли: локальная и интегральная формула Муавра-Лапласса. Формула Пуассона.
- •13. Отклонение относительной частоты от постоянной вероятности. Закон больших чисел в формуле Бернулли.
- •14. Случайные величины: дискретные и непрерывные
- •15. Закон распределения дискретной случайной величины. Многоугольник (полигон) распределения.
- •16. Неперывная случайная величина. Функция распределения, ее свойства. Плотность распределения, ее свойства.
- •17. Числовые характеристики случайных величин и их свойства.
- •19. Правило трех сигм
- •22. Эмпирическая функция распределения: полигон и гистограмма.
- •23. Числовые характеристики выборки.
- •28. Коэффициент корреляции. Его основные свойства и статистический смысл.
- •29. Задачи регрессионного анализа. Линейная регрессия.
5. Частота события. Статистическое определение вероятности. Понятие устойчивости и законе больших чисел. Недостатки определения.
Частота
события x — отношение N(x)
/ N числа N(x) наступлений этого
события в N испытаниях к числу
испытаний N. Очевидно, что
 Определяется экспериментально (в
большинстве случаев). При рассмотрении
результатов отдельных испытаний очень
трудно найти какие-либо закономерности.
Однако в последовательности одинаковых
испытаний можно обнаружить устойчивость
некоторых средних характеристик.
Частостью какого-либо события в данной
серии из n испытаний называется
отношение m/n, числа m тех испытаний,
в которых событие А наступило, к
общему числу испытаний n. Почти в
каждой достаточно длинной серии испытаний
частость события А устанавливается
около определенного значения
Определяется экспериментально (в
большинстве случаев). При рассмотрении
результатов отдельных испытаний очень
трудно найти какие-либо закономерности.
Однако в последовательности одинаковых
испытаний можно обнаружить устойчивость
некоторых средних характеристик.
Частостью какого-либо события в данной
серии из n испытаний называется
отношение m/n, числа m тех испытаний,
в которых событие А наступило, к
общему числу испытаний n. Почти в
каждой достаточно длинной серии испытаний
частость события А устанавливается
около определенного значения
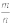 ,
которое принимается за вероятность
события А. Устойчивость значения
частости подтверждается специальными
экспериментами. Статистические
закономерности такого рода были впервые
обнаружены на примере азартных игр, т.
е. на примере тех испытаний, которые
характеризуются равновозможностью
исходов. Это открыло путь для статистического
подхода к численному определению
вероятности, когда нарушается условие
симметрии эксперимента. Частость события
А называют статистической
вероятностью, которая обозначается
,
которое принимается за вероятность
события А. Устойчивость значения
частости подтверждается специальными
экспериментами. Статистические
закономерности такого рода были впервые
обнаружены на примере азартных игр, т.
е. на примере тех испытаний, которые
характеризуются равновозможностью
исходов. Это открыло путь для статистического
подхода к численному определению
вероятности, когда нарушается условие
симметрии эксперимента. Частость события
А называют статистической
вероятностью, которая обозначается
|
(1.2) |
где mA - число экспериментов, в которых появилось событие А; n - общее число экспериментов.
Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду. Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
6. Алгебра событий. Аксиоматическое определение вероятности. Свойства вероятности из аксиоматического определения.
Аксиоматическое определение вероятности
Пусть Ω -
множество всех возможных исходов
некоторого опыта (эксперимента). Согласно
аксиоматическому определению вероятности,
каждому события А (А подмножество
множества Ω) ставится в соответствии
некоторое числу р(А), называемое
вероятностью события А, причем так, что
выполняются следующие три условия
(аксиомы вероятнос тей):
тей):
р(А)≥0
p(Ω)=1
аксиома сложения
где Аi·Aj=Ω (i≠j), т.е. вероятность суммы попарно-несовместных событий равна сумме вероятностей этих событий.
Из этих трех аксиом, вытекают свойства вероятности:
р(Ø)=0, т.е. вероятность невозможного события равна нулю.
р(А)+р(Ā)=1
0≤р(А)≤1 для любого события А
р(А)≤р(В), если А подмножество В
 ,
если
,
если
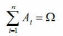 и
Аi·Aj=Ø, i≠j
и
Аi·Aj=Ø, i≠j
Если множество Ω состоит из n равновозможных элементарных событий, то вероятность события А определяется по формуле классического определения вероятности:
p(A)=m/n
где m - число случаев (элементов), принадлежащих множеству В (число блогаприятствующих событию А исходов), n - число элементов множества Ω (число всех исходов опыта).
Система событий называется АС если выполняются условия:
|
пространство элементарных событий (W) принадлежит системе событий |
|
если событие (A) принадлежит системе событий, то и его отрицание также принадлежит системе событий |
|
если два (А и В) события принадлежат системе событий, то их произведение (АВ) и сумма (А+В) также принадлежат системе событий |
7. Теорема
сложения вероятностей. НЕСОВМЕСТНЫЕ
СОБЫТИЯ - Вероятность суммы конечного
числа несовместных событий
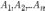 равна
сумме вероятностей этих событий
равна
сумме вероятностей этих событий
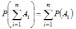 (2.1)
(2.1)
Доказательство.
Докажем эту теорему для случая суммы
двух несовместных событий
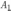 и
и
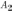 .
Пусть событию
благоприятствуют
.
Пусть событию
благоприятствуют
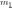 элементарных
исходов, а событию
элементарных
исходов, а событию
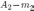 исходов.
Так как события
и
по
условию теоремы несовместны, то событию
исходов.
Так как события
и
по
условию теоремы несовместны, то событию
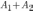 благоприятствуют
благоприятствуют
 элементарных
исходов из общего числа n исходов.
Следовательно,
элементарных
исходов из общего числа n исходов.
Следовательно,
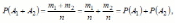 ,
,
где
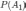 —
вероятность события
—
вероятность события
 ;
;
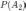 —
вероятность события
.
—
вероятность события
.
Теорема сложения вероятностей совместных событий
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же опыте.
Пример.
Поступление в магазин одного вида товара
— событие
.
Поступление второго вида товара —
событие
 .
Поступить эти товары могут и одновременно.
Поэтому
и
-
совместные события.
.
Поступить эти товары могут и одновременно.
Поэтому
и
-
совместные события.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
P(A+B) = P(A) + P(B) — P(AB). (2.5)
Доказательство.
Событие
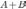 наступит,
если наступит одно из трех несовместных
событий
наступит,
если наступит одно из трех несовместных
событий
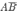 ,
, ,
,
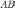 .
По теореме сложения вероятностей
несовместных событий имеем
.
По теореме сложения вероятностей
несовместных событий имеем
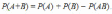 (2.6)
(2.6)
Событие
произойдет,
если наступит одно из двух несовместных
событий:
,
.
Вновь применяя теорему сложения
вероятностей несовместных событий,
получаем
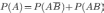 .
Откуда
.
Откуда
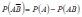 (2.7)
(2.7)
Аналогично
для события
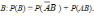 Откуда
Откуда
 .(2.8)
.(2.8)
Подставив (2.7) и (2.8) в (2.6), находим
P(A+B) = P(A) + P(B) — P(AB).
Пример. Если вероятность поступления в магазин одного вида товара равна P(A) = 0,4, а второго товара — P(B) = 0,5, и если допустить, что эти события независимы, но совместны, то вероятность суммы событий равна
P(A+B) = 0,4 + 0,5 — 0,4×0,5 = 0,7.

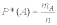 ,
,