1.6.3. Квазиклассическое приближение.

Переход от квантового описания системы к квазиклассическосму проведем следующим образом. Внутренняя энергия макроскопических систем меняется непрерывно, и квантовые эффекты не имеют существенного значения (см. раздел 1.3 и формулу (1.35) при 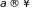). Из распределения Гиббса следует, что для замены ступенчатой функции плавной – необходимо, чтобы интервалы между энергиями были малы по сравнению с . Это означает, что переход к квазиклассической статистике должен происходить при прочих равных условиях в области высоких температур .

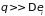Состояние системы, состоящей из частиц и имеющей степеней свободы, в квазиклассическом приближении определяется значениями координат ( ) и импульсов ( ). Ее энергия является непрерывной функцией всех координат и импульсов 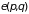. Это позволяет говорить о непрерывном распределении вероятностей того, что система находится в одном из состояний в интервале энергий между и 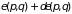. Учитывая, что согласно (1.40), число таких состояний равно 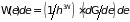, распределение Гиббса в квазиклассическом приближении принимает вид

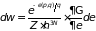, (1.61)

где

(1.62)

Отличие этой формулы от (1.59) состоит в том, что сумма по состояниям заменена интегралом. Интегрирование ведется по всему фазовому пространству, доступному для системы, т.е. по всем дозволенным значениям координат и импульсов системы.

1.7. Свойства распределения Гиббса

Область применения распределения Гиббса ограничена следующими условиями:

1) система находится в равновесном состоянии;

2) наличие макроскопической системы (термостата), составляющей ее окружение (термостата);

3) слабое взаимодействие между системой и термостатом.

В остальном свойства системы произвольны, в частности, не зависят от характера взаимодействия и ее агрегатного состояния.

Поскольку статистическая температура положительная величина (1.57б), то энтропия, а, следовательно, и число состояний (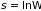 ) являются монотонно возрастающей функцией энергии. Чем больше частиц содержит система, тем больше состояний , отвечает данному значению интервала энергии 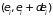. С ростом энергии (увеличением квантового числа ) резко возрастает плотность энергетических уровней (1.35б). Поэтому рост с энергией происходит тем быстрее, чем больше частиц в системе.

Чтобы выяснить характер зависимости распределения Гиббса 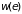от энергии, необходимо вычислить производную 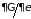(1.61). Расчеты проведем для ансамбля молекул идеального газа. Объем части фазового пространства, в котором энергия газа не превышает , по определению, равен интегралу

,

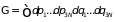где пределы интегрирования следуют из условия

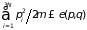. (1.63)

Оно не включает координаты молекул, по которым можно интегрировать непосредственно

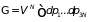, (1.64)

поскольку для каждой молекулы можно написать

.

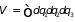С геометрической точки зрения формула (1.63) определяет в импульсном пространстве измерений шар, радиус которого равен , а интеграл в (1.64) представляет его объем. В трехмерном пространстве объем пропорционален 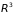, т.е. 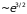. Исходя из соображений размерности в –мерном пространстве он пропорционален . Поэтому из (1.64) следует

.

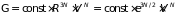После дифференцирования имеем

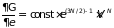(1.65)

Постоянная не имеет особого значения, поскольку оно будет сокращаться с такой же постоянной, возникающей при вычислении 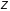. Поэтому распределение Гиббса принимает вид

.

Поскольку множите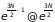ль весьма быстро растет с увеличением , а множитель 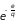, напротив, резко убывает, функция распределения Гиббса для макроскопических систем ( моль^-1) имеет очень резкий максимум, степень его размытости совершенно ничтожна. Это означает, что вероятность нахождения системы в состояниях с энергией, заметно отличающейся от энергии 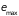, отвечающей максимуму распределения Гиббса, практически равна нулю (рис. 1.5). Такой характер зависимости позволяет в первом приближении отождествить ее с 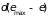–дельта функцией Дирака, которая определяется для непрерывной функции при

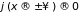
	операторным соотношением . В макросистемах практически совпадает со средним значением энергии . Поэтому средняя величина какого-либо физического параметра макроскопической системы есть функция средней энергии
Рис. 1.5.

. (1.67)

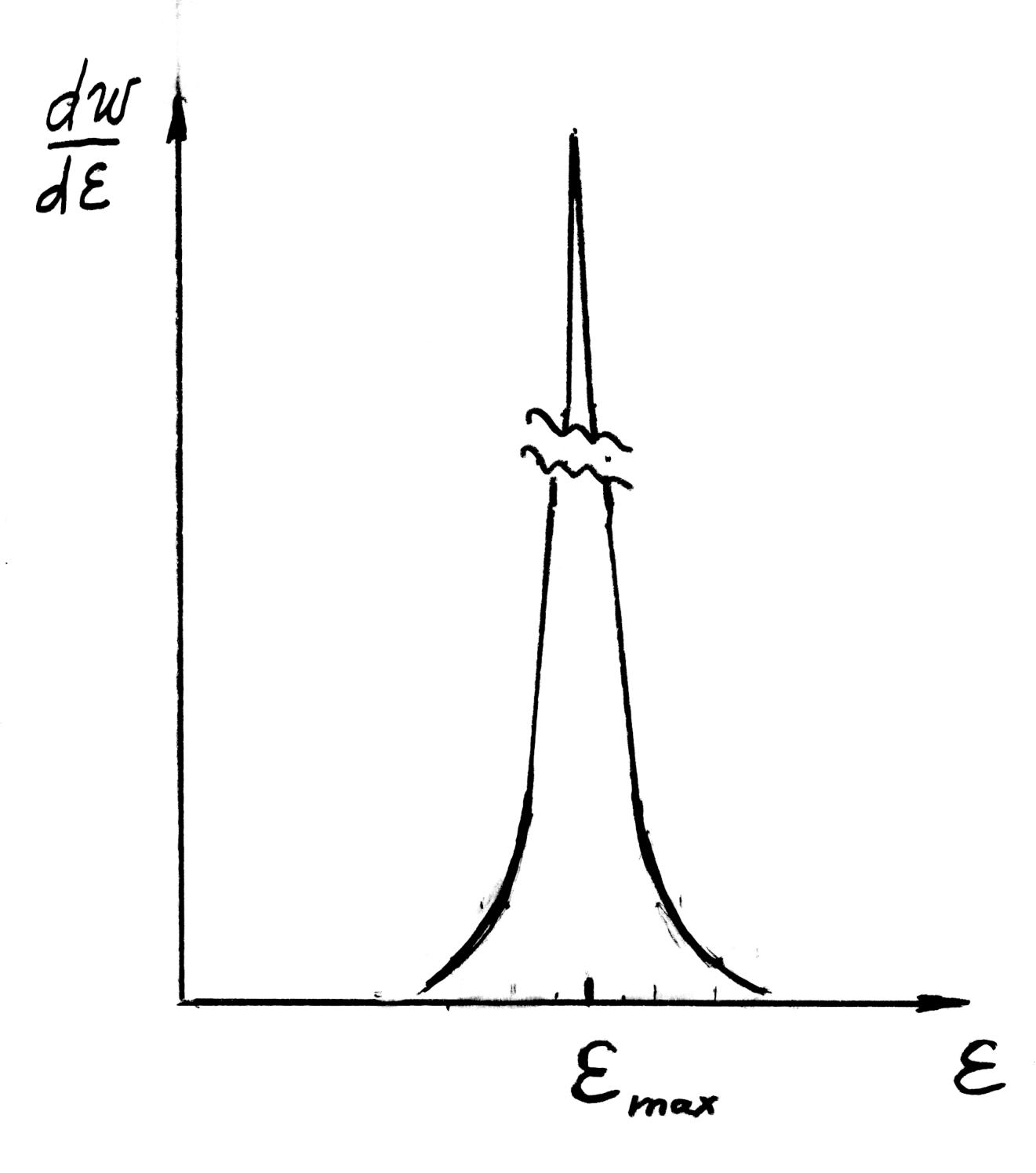
По сути это означает, что состояние с энергией 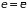осуществляется с полной достоверностью, а при остальных энергиях невозможно .