
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
2.4. Характерные величины идеального газа
2.4.1. Свойства
распределения Максвелла. На рис.
2.2 и 2.3 изображена функция распределения
по проекциям и абсолютной величине
скорости (2.4), (2.6). По оси ординат отложены
значения
 и
и
 ,
а по оси абсцисс – величины
,
а по оси абсцисс – величины
 и
и
 ,
соответственно. В первом случае
(рис. 2.2) кривая
,
соответственно. В первом случае
(рис. 2.2) кривая
|
|
Рис. 2.2. |
Рис. 2.3. |
распределения
симметрична по отношению к положительным
и отрицательным значениям
,
имеет максимум при
 и асимптотически обращается в нуль при
стремлении аргумента к бесконечности.
Кривая распределения по абсолютным
значениям скоростей (рис. 2.3) обращается
в нуль при
и асимптотически обращается в нуль при
стремлении аргумента к бесконечности.
Кривая распределения по абсолютным
значениям скоростей (рис. 2.3) обращается
в нуль при
 ,
проходит через максимум и асимптотически
стремится к нулю при бесконечно больших
значениях скоростей. Таким образом,
число молекул в газе с очень малыми и
очень большими абсолютным скоростями
оказывается сравнительно небольшим.
Формулы позволяют найти число очень
быстрых и очень медленных молекул. С
ростом температуры распределение
становится более пологим: относительное
число молекул с большими значениями
скоростей возрастает.
,
проходит через максимум и асимптотически
стремится к нулю при бесконечно больших
значениях скоростей. Таким образом,
число молекул в газе с очень малыми и
очень большими абсолютным скоростями
оказывается сравнительно небольшим.
Формулы позволяют найти число очень
быстрых и очень медленных молекул. С
ростом температуры распределение
становится более пологим: относительное
число молекул с большими значениями
скоростей возрастает.
2.4.2. Опыт Штерна. Распределение Максвелла суть – частный случай канонического распределения Гиббса, которое получено из теоретической модели, исходя из общих физических предположений. Непосредственная его проверка невозможна. Поэтому экспериментальная проверка распределения Максвелла имеет принципиальное значение – является одной из важнейших задач молекулярной физики. Существуют разные методы измерения распределения молекул по скоростям; здесь рассмотрим опыт Штерна.
Модель его установки
показана на рис. 2.4. В качестве объекта
исследования используют пары металлов
(висмут, кадмий, цезий и др.), которые
испаряются из плавильной печи (1) в
вакуум. Через систему щелей ( ,
,
 )
из них формируется узкий молекулярный
пучок (выделяются молекулы имеющие одну
компоненту скорости, например,
).
На пути пучка устанавливаются два
синхронно вращающихся цилиндра (2) и
(3), радиусы которых отличаются на величину
,
а внутренний имеет небольщую прорезь.
Пучок достигает поверхности внешнего
цилиндра (3), если щель во внутреннем
цилиндре находится против щелей в
экранах
и
.
При
)
из них формируется узкий молекулярный
пучок (выделяются молекулы имеющие одну
компоненту скорости, например,
).
На пути пучка устанавливаются два
синхронно вращающихся цилиндра (2) и
(3), радиусы которых отличаются на величину
,
а внутренний имеет небольщую прорезь.
Пучок достигает поверхности внешнего
цилиндра (3), если щель во внутреннем
цилиндре находится против щелей в
экранах
и
.
При
|
бесконечной
скорости ( |
Рис. 2.4. |
 от точки
.
В процессе эксперимента на внутренней
поверхности внешнего цилиндра (охлаждается
жидким воздухом!) образуется слой из
осевших молекул, толщина которого
отражает обратное распределение
Максвелла. Измеренная фотометрическим
методом толщина слоя как функция смещения
подтвердила распределение Максвелла
по скоростям.
от точки
.
В процессе эксперимента на внутренней
поверхности внешнего цилиндра (охлаждается
жидким воздухом!) образуется слой из
осевших молекул, толщина которого
отражает обратное распределение
Максвелла. Измеренная фотометрическим
методом толщина слоя как функция смещения
подтвердила распределение Максвелла
по скоростям.
В отличие от распределения Гиббса распределение Максвелла изображается размытой кривой. Это обусловлено тем, что в моделях рассматривались разные системы. Распределения Гиббса относится к системам с очень большим числом частиц (ширина размытости обратно пропорциональна их числу), а распределение Максвелла – к системам с одной частицей.
2.4.3. Средние скорости и энергия молекул. Из распределения Максвелла можно найти средние значения любых величин, характеризующих свойства газовых молекул. Например, среднее значение компоненты скорости:
 .
.
Этот результат
очевиден, если учесть равновероятность
движения молекул в двух противоположных
направлениях. Аналогичные вычисления
дают
 ,
а следовательно,
,
а следовательно,
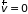 .
Среднее значение абсолютной скорости
определим, учитывая распределение (2.6)
и интервал изменения
.
Среднее значение абсолютной скорости
определим, учитывая распределение (2.6)
и интервал изменения
 :
:
 . (2.11)
. (2.11)
Из условия

найдем наиболее вероятную скорость молекул газа, при которой максвелловское распределение имеет максимум:
 (2.12)
(2.12)
В соответствии с полученными формулами средняя и наиболее вероятная скорости молекул возрастают с ростом температуры и обратно пропорционально корню квадратному из массы молекулы.
Вычисления

определяют среднюю кинетическую энергию поступательного движения газовой молекулы
 . (2.13)
. (2.13)
Она не зависит от природы молекулы и пропорциональна температуре газа . Средняя (внутренняя) энергия газа, равна сумме энергий всех его молекул:
 , (2.14)
, (2.14)
где – полное число молекул в газе. Средняя энергия механического движения молекул газа отождествляется с макроскопической тепловой энергией. С кинетической точки зрения абсолютная температура есть величина, характеризующая среднюю энергию движения молекул.
В силу равноправия
всех направлений в пространстве средняя
энергия движения молекулы в каждом
направлении должна быть одинаковой. Но
поскольку каждая молекула имеет три
степени свободы, и ее движение может
быть разложена на движение в трех взаимно
перпендикулярных направлениях, то из
формулы (2.13) следует, что на каждую
степень свободы в среднем приходится
энергия, равная
 .
Это утверждение – частный случай весьма
общего закона о равномерном распределении
энергии по степеням свободы в классических
системах. Кроме поступательного движения
этому закону подчиняется и вращательное
движение. Особый случай представляет
колебательное движение, где на каждую
степень свободы приходится энергия –
.
Это утверждение – частный случай весьма
общего закона о равномерном распределении
энергии по степеням свободы в классических
системах. Кроме поступательного движения
этому закону подчиняется и вращательное
движение. Особый случай представляет
колебательное движение, где на каждую
степень свободы приходится энергия –
 .
.
Установим связь
между внутренней энергией газа
и его давлением
 .
Поскольку
.
Поскольку
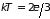 (2.13), то давление
(2.13), то давление
 (2.15)
(2.15)
оказывается
численно равным
 кинетической энергии поступательного
движения молекул газа, находящихся в
единице объема.
кинетической энергии поступательного
движения молекул газа, находящихся в
единице объема.
Вычисления среднего
квадрата энергии (2.7) и её квадратичной
флуктуации ( )
дают:
)
дают:
 ;
;
 ;
;
 .
.
Большая относительная флуктуация обусловлена тем, что оно относится к отдельной молекуле. Если же рассматривать газ из молекул, то его средняя энергия, дисперсия и относительная флуктуация оказываются равными
 ;
;
 ;
;
 . (2.16)
. (2.16)
В этом случае отличие истинного значения энергии от его среднего ничтожно мало при всех реальных значениях . Следовательно можно с большой степенью точности считать энергию идеального газа равной ее среднему значению.



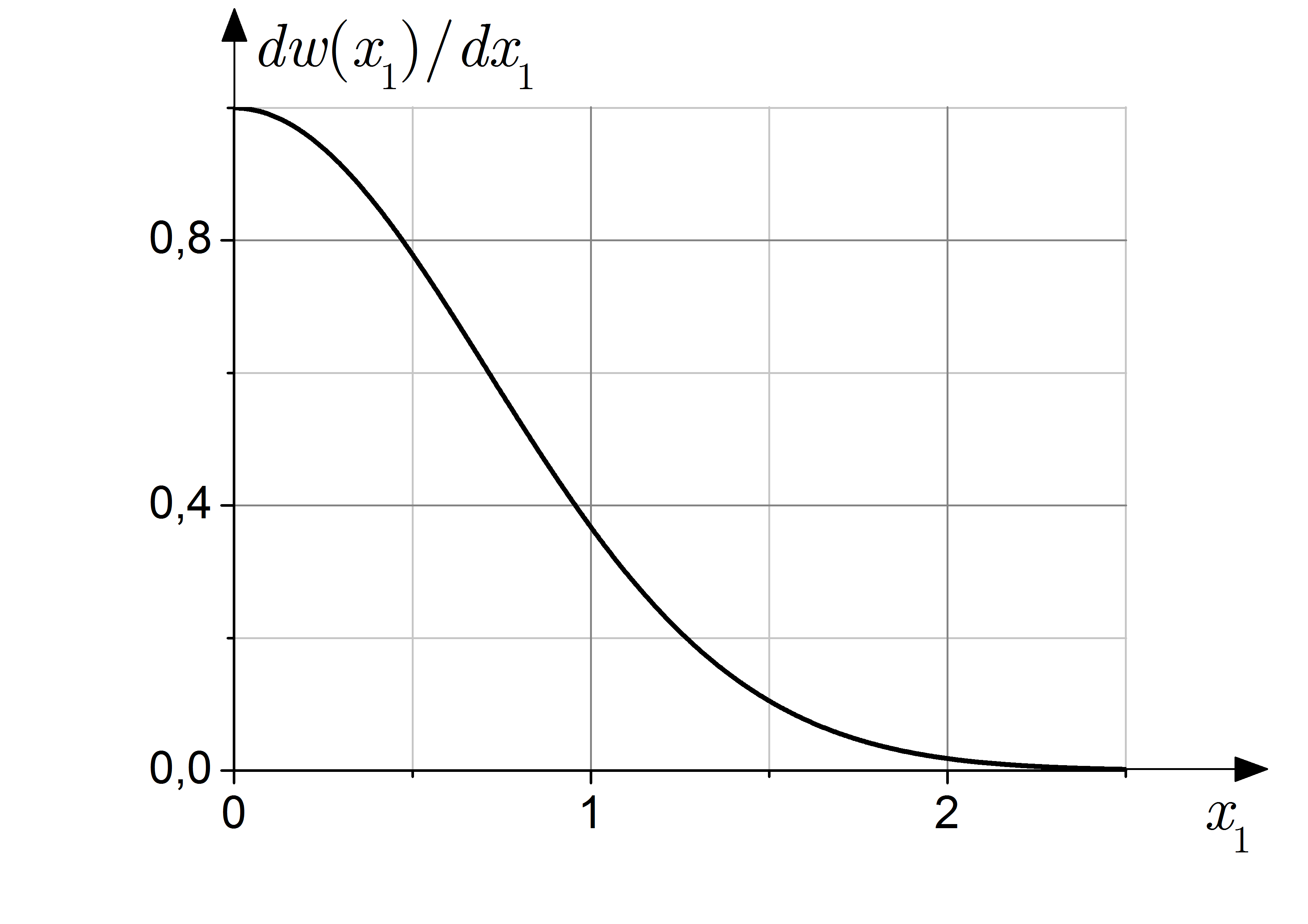





 )
молекулы оседали бы в точке
,
находящейся против щели внутреннего
цилиндра. Но поскольку молекулы имеют
разные скорости, то они оседают в точке
)
молекулы оседали бы в точке
,
находящейся против щели внутреннего
цилиндра. Но поскольку молекулы имеют
разные скорости, то они оседают в точке
 ,
расстояние которой от точки
зависит от их скорости. Оно увеличивается
с уменьшением скорости. При заданной
угловой скорости вращения цилиндров
,
расстояние которой от точки
зависит от их скорости. Оно увеличивается
с уменьшением скорости. При заданной
угловой скорости вращения цилиндров
 частицы, летящие по инерции в пространстве
между цилиндрами, оседают на расстоянии
частицы, летящие по инерции в пространстве
между цилиндрами, оседают на расстоянии