1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.

Движение каждой частицы определено законами механики (в первом приближении – классической механики). Поэтому, интегрируя уравнения движения всех частиц системы, можно было бы найти траекторию каждой из них. Однако фактически подобного рода расчет сталкивается с огромными техническими и принципиальными трудностями. В изучаемых макроскопических системах с весьма большим числом взаимодействующих частиц (в газе моль^–1) для нахождения их траекторий нужно было бы записать и разрешить связанных между собой уравнений движения при соответствующих начальных условиях. Хотя каждая из частиц является «механической системой», в совокупности их огромного числа проявляются закономерности особого рода, совершенно не свойственные простым механическим системам. Если измерять манометром давления газа в сосуде при постоянных внешних условиях, то его показания сохраняются, хотя за время измерения каждая частица много раз меняет скорость и свое положение в пространстве. Движение отдельной частицы, ее траектория и последовательность изменения состояний становится несущественной деталью явления. Его нельзя изучать вне связи с движением всех остальных частиц. Свойства таких систем, как правило, не определяются их начальным состоянием. Так, например, свойство газа в сосуде не зависят от того, каким образом в начальный момент времени сосуд был заполнен газом. В этом принципиальное отличие систем, подчиняющихся статистическим закономерностям, от механических систем, движение которых подчиняется динамическим законам. Характерной чертой статистической физики является представление о динамических переменных как о случайных величинах, которым присущи определенные вероятности появления при испытаниях, и в этом заключается качественно новый подход к описанию систем по сравнению с чисто механическим. Хотя движение отдельной частицы оказывает малое влияние на поведение статистической системы, свойства и закон ее движения существенно отражаются на свойствах макроскопических систем. Синтез механических и вероятностных представлений лежит в основе анализа общих свойств и закономерностей макроскопических процессов.

Определим, как связано термодинамическое (макроскопическое) состояние системы с известными микроскопическими состояниями, в которых она может находиться. Рассмотрим изолированную макросистему с степенями свободы и энергией , состояние которой определяется каноническими координатами 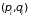. Эволюцию ее состояний со временем отражает фазовая траектория, фрагмент которой схематически показан на рис. 1.3. Если следить за системой в течение достаточно большого времени ( ), то она может побывать во всех точках фазового пространства, а также внутри выделенного малого объема . Последний отвечает значениям координат между и , т.е. некоторому термодинамическому состоянию системы. Очевидно, что чрезвычайно запутанная в общем случае траектория много раз пройдет через выделенный участок фазового пространства. Пусть – суммарное время нахождения системы в объеме . Если – общее время наблюдения, то существует предел

	, который можно трактовать как вероятность, что в произвольный момент времени система находится в состоянии, определенном элементом объема . Эта вероятность может быть вычислена также теоретически путем интегрирования уравнений движения с учетом начальных условий.
Рис. 1.3.

Проведем эти расчеты иным способом. Вместо непрерывного наблюдения будем фиксировать состояние системы через малые промежутки времени ( ); каждое такое состояние отображается точками в фазовом пространстве (рис. 1.3.), распределенными с некоторой плотностью. Вместо того, чтобы рассматривать изобразительные точки одной системы в различные моменты времени, введем в рассмотрение очень большое (в пределе бесконечное) число тождественных систем, находящихся в некоторый момент времени в состояниях . Это множество одинаковых систем, отражающих эволюцию состояний одной системы, обычно называют статистическим (фазовым) ансамблем (ансамблем Гиббса). Такой метод позволяет определить вероятность нахождения системы в данный момент времени в элементе фазового объема как предел отношения числа систем фазового ансамбля в объеме к их общему числу

;

индекс говорит о размерности фазового пространства ( ). При его бесконечно малом объеме

.

Функция 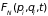– имеет смысл плотности распределения вероятности (функции статистического распределения).

Если система состоит из тождественных частиц, то ее микросостояния (изобразительные точки), которые реализуются при данном макросостоянии, заполняют некоторый объем . В этом случае статистическим ансамблем является тождественных частиц в течение бесконечно малого промежутка времени наблюдения. Пусть – число частиц, фазовые координаты которых попадают в объем , тогда вероятность нахождения системы в этом объеме есть отношение

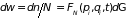. (1.42)

Таким образом, введя в рассмотрение фазовый ансамбль, задачу механики свели к статистической – нахождению функции распределения.

Через весьма небольшой промежуток времени , за который координаты и импульсы частиц изменяются незначительно [ , ], система в результате движения перейдет из объема в объем . Для ансамбля, подчиняющегося уравнениям Гамильтона, плотность числа фазовых точек не изменяется при своем движении вдоль фазовой траектории 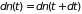, т.е. элементы фазового объема перемещаются как несжимаемая жидкость. Поэтому из (1.42) имеем

. (1.43)

Уравнение справедливо в течение промежутка времени, когда систему можно считать замкнутыми. Согласно теореме Лиувилля (см. Приложение 2), элементарный объем в фазовом пространстве, перемещаясь с течением времени, остается постоянным по величине, хотя его форма может меняться, т.е. . Это одно из основных положений статистической механики. Действительно, если в какой-либо момент времени вероятность нахождения фазовой точки в определенном элементе объема фазового пространства известна, то она будет известна и для любого другого момента времени. В силу этого становится возможным вместо начальных условий, используемых в механике, принять статистическое предположение о равновероятности состояний, изображаемых элементами фазового пространства равного объема. Эти замечания позволяют вместо (1.43) записать , а после разложения в ряд Маклорена правой части равенства с учетом уравнений движения Гамильтона (1.11) получаем уравнение для функции распределения

. (1.44)

В стационарном состоянии из равенства нулю скобок Пуассона 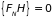непосредственно следует, что функция распределения должна быть интегралом движения (1.14) и выражаться через такие комбинации переменных и , которые с течением времени остаются постоянными. Иными словами, она есть функция механических интегралов движения . Если система как целое не совершает поступательного движения (количество движения ) и не вращается (момент количества движения ), то функция распределения и состояние системы определяются ее энергией .

В заключение отметим следующее. Явный вид функции определенным образом должен зависеть от тех моделей, на основе которых описывается поведение частиц системы, а именно: классической или квантовой. Далее следует учитывать особенности взаимодействия системы с окружением. Его можно представить исчезающее малым и тогда для такой замкнутой (изолированной) системы , . Чаще всего исследуется квазизамкнутая система с постоянным числом частиц , но . Наконец, самый общий случай взаимодействия системы с окружением учитывает обмен энергией ( ) и числом частиц ( ).

Указанные особенности системы и принятая модель частиц определяют функцию распределения и, в конечном счете, различные её средние физико-химические свойства. Сравнение результатов расчета с опытом позволяют сделать вывод о правильности принятой модели вещества и характере взаимодействия системы с окружением.