- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
4.3. Кристалл как система линейных гармонических осцилляторов
Тепловое
движение в трехмерном кристалле имеет
такой же характер, что и в одномерной
модели. Смещение одного атома из положения
равновесия в решетке передается его
ближайшим соседям в трех направлениях,
поэтому в кристалле возникают упругие
волны, распространяющиеся в трех
направлениях. В результате их отражения
от граней в кристалле установится
система стоячих волн. Такая аналогия с
одномерной моделью позволяет и в этом
случае описать движение атомов через
суперпозицию трехмерных нормальных
колебаний. Функция состояния кристалла
зависит от его энергии, которая состоит
из потенциальной (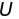 )
и кинетической (
)энергии
колебаний всех атомов
)
и кинетической (
)энергии
колебаний всех атомов
 .
.
Вычислим сначала
энергию одномерного кристалла. Выразим
смещения атомов в нормальных колебаниях
через обобщенные координаты
 ,
которые обладают независимой друг от
друга динамикой. Тогда смещение
-го
атома (4.4) можно представить в виде
,
которые обладают независимой друг от
друга динамикой. Тогда смещение
-го
атома (4.4) можно представить в виде
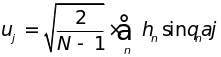 .
.
Энергия цепочки атомов равна
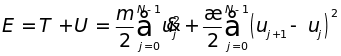 ,
,
где суммирование
ведется по всем атомам цепочки. Подстановка
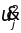 дает
дает
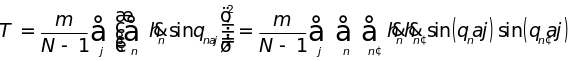 .
.
После изменения порядка суммирования
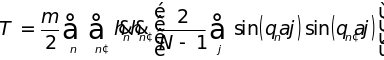 .
.
В силу ортогональности синусов
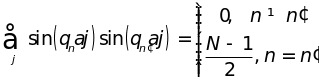
имеем
 .
.
Для определения потенциальной энергии вычислим

Поступая так же, как при вычислении кинетической энергии, с учетом ортогональности косинусов получаем

Таким образом, полная энергия одномерного кристалла
 (4.8)
(4.8)
выражается
квадратичной формой (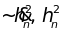 ).
Каждое слагаемое
).
Каждое слагаемое
 (4.9)
(4.9)
представляет энергию линейного гармонического осциллятора с массой, равной массе атома, колеблющегося с частотой . Энергия кристалла из атомов, совершающих связанные колебания, оказывается равной энергии независимых гармонических осцилляторов. В этом смысле кристалл из связанных атомов эквивалентен набору независимых осцилляторов с частотами . Вместо того, чтобы находить среднюю энергию сложной системы колеблющихся связанных атомов, можно ее определить из простой эквивалентной системы – набора независимых осцилляторов. Каждый осциллятор – одно из нормальных колебаний кристалла, в котором участвуют все атомы.
В квантовой механике энергия линейного осциллятора принимает дискретный ряд значений:
 ,
,
 , (4.10)
, (4.10)
где
 – квантовое число,
– классическая частота, связанная с
постоянной упругой силы и массой атома.
Энергетический спектр осциллятора
состоит из совокупностей дискретных
уровней, отстоящих друг от друга на
величину
– квантовое число,
– классическая частота, связанная с
постоянной упругой силы и массой атома.
Энергетический спектр осциллятора
состоит из совокупностей дискретных
уровней, отстоящих друг от друга на
величину
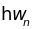 .
Минимальная порция (квант)
энергии
.
Минимальная порция (квант)
энергии
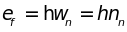 ,
которую может поглотить (испустить)
кристалл при тепловых колебаниях,
называется фононом. В таких процессах
происходит переход возбуждаемого
нормального колебания с данного уровня
на ближайший соседний. Поле упругих
волн можно трактовать как газ, образованный
квантами нормальных колебаний решетки
– фононами, обладающими энергией
,
которую может поглотить (испустить)
кристалл при тепловых колебаниях,
называется фононом. В таких процессах
происходит переход возбуждаемого
нормального колебания с данного уровня
на ближайший соседний. Поле упругих
волн можно трактовать как газ, образованный
квантами нормальных колебаний решетки
– фононами, обладающими энергией
 и импульсом
и импульсом
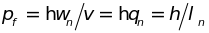 .
Иными словами, нагретый кристалл можно
уподобить ящику, заполненному фононным
газом.
.
Иными словами, нагретый кристалл можно
уподобить ящику, заполненному фононным
газом.
4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
Уровни энергии
всего кристалла совпадают с уровнями
энергии набора
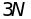 независимых гармонических осцилляторов.
Общая энергия есть сумма слагаемых вида
(4.10), где
принимает значения
независимых гармонических осцилляторов.
Общая энергия есть сумма слагаемых вида
(4.10), где
принимает значения
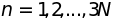 .
Если
.
Если
 – потенциальная энергия кристалла в
равновесном состоянии, то энергия
колебаний всех осцилляторов кристалла
в соответствующих состояниях
– потенциальная энергия кристалла в
равновесном состоянии, то энергия
колебаний всех осцилляторов кристалла
в соответствующих состояниях
 ,
,
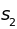 ,
…,
,
…,
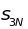 равна:
равна:
 , (4.11)
, (4.11)
где
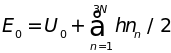 – есть энергия нулевых колебаний.
Состояние каждого осциллятора (
-ой
моды нормальных колебаний) определяется
полным набором целых чисел. Сумма по
всем этим состояниям в ансамбле
осцилляторов дает функцию состояний
кристалла
– есть энергия нулевых колебаний.
Состояние каждого осциллятора (
-ой
моды нормальных колебаний) определяется
полным набором целых чисел. Сумма по
всем этим состояниям в ансамбле
осцилляторов дает функцию состояний
кристалла
 ;
;
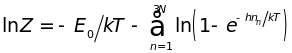 . (4.12)
. (4.12)
Отсюда легко найти свободную и внутреннюю энергии
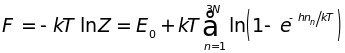 , (4.13)
, (4.13)
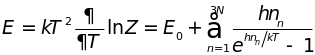 . (4.14)
. (4.14)
Каждое слагаемое в сумме имеет смысл средней энергии осциллятора -ой моды
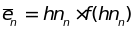 . (4.15)
. (4.15)
Функция
 (4.16)
(4.16)
определяет среднее
число фононов (распределение
Бозе-Эйнштейна). От тепловой энергии
зависит число возбуждаемых фононов
данной частоты
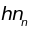 .
.
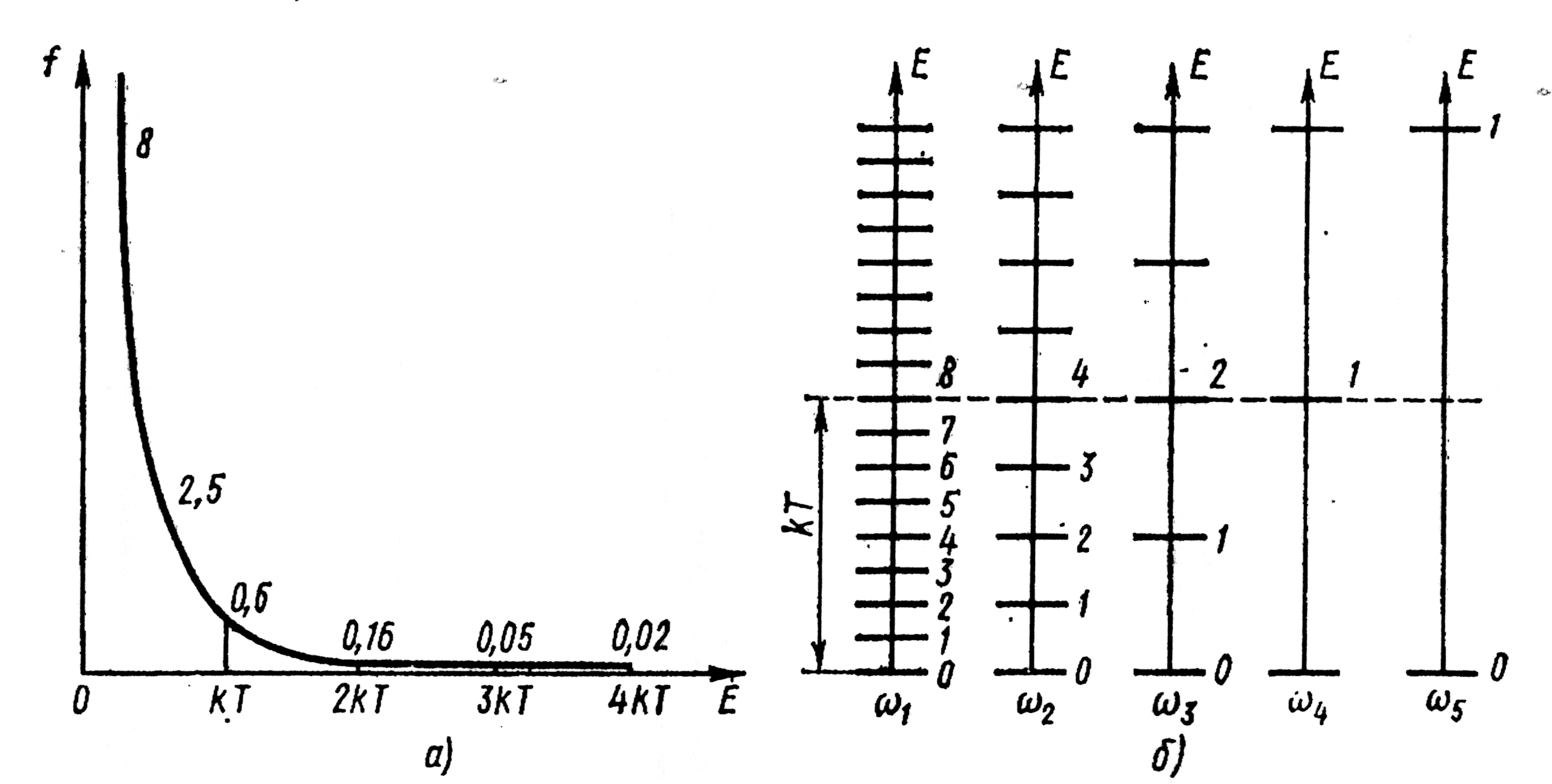
|
Рис. 4.3 |
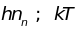 ,
колебания с энергией
,
колебания с энергией
 практически не возбуждаются (Рис. 4.3,а).
На рис. 4.3,б горизонтальными черточками
отмечены энергетические спектры
нормальных колебаний, имеющие частоты
практически не возбуждаются (Рис. 4.3,а).
На рис. 4.3,б горизонтальными черточками
отмечены энергетические спектры
нормальных колебаний, имеющие частоты
 ,
,
 ,
,
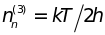 ,
,
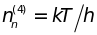 ,
,
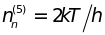 .
.
Видно, что колебание
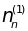 возбуждено до 8-го уровня,
возбуждено до 8-го уровня,
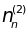 – до 4-го, …, а
– до 4-го, …, а
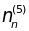 вообще не возбуждается при данной
температуре.
вообще не возбуждается при данной
температуре.
К сожалению,
приведенные формулы, кроме качественных
оценок свойств кристалла, не позволяют
делать количественные расчеты. Трудности
заключаются в том, что частоты
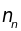 остаются неизвестными, их определение
для обобщающей модели кристалла – ключ
к построению его статистико-механической
теории. В принципе для отдельных тел
можно определить из дисперсионного
уравнения с учетом силовых постоянных.
Недостаток такого подхода в том, что,
во-первых, силовые параметры для
большинства реальных кристаллов измерены
с большой погрешностью, с другой стороны,
в необходимости проводить численные
расчеты для каждого отдельного кристалла.
Таким образом, теряется простота и
общность результатов статистической
термодинамики, фундаментальность
которой основана на едином наборе
обобщающих уравнений.
остаются неизвестными, их определение
для обобщающей модели кристалла – ключ
к построению его статистико-механической
теории. В принципе для отдельных тел
можно определить из дисперсионного
уравнения с учетом силовых постоянных.
Недостаток такого подхода в том, что,
во-первых, силовые параметры для
большинства реальных кристаллов измерены
с большой погрешностью, с другой стороны,
в необходимости проводить численные
расчеты для каждого отдельного кристалла.
Таким образом, теряется простота и
общность результатов статистической
термодинамики, фундаментальность
которой основана на едином наборе
обобщающих уравнений.
Модель
Эйнштейна. В
общем случае при определении спектра
нормальных колебаний произвольных
систем использовались упрощающие
модели. Согласно приближенной модели
Эйнштейна, каждый атом, колеблющийся в
узле кристаллической решетки,
отождествлялся с квантовым осциллятором,
имеющим три степени свободы. В кристалле
с атомами одного сорта все атомы
совершенно равноправны и колеблются
независимо друг от друга с одинаковой
частотой
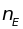 .
В этом случае энергия линейного
гармонического осциллятора равна
.
В этом случае энергия линейного
гармонического осциллятора равна
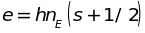 ,
а его функция состояния
,
а его функция состояния
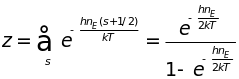 .
.
Средняя энергия колебательного движения атома с одной степенью свободы и кристалла из атомов равны
 (4.17)
(4.17)
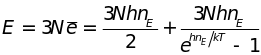 . (4.18)
. (4.18)
Непосредственно дифференцируя (4.18), получаем формулу Эйнштейна
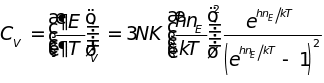 . (4.19)
. (4.19)
При
высоких температурах (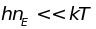 )
значение теплоемкости соответствует
закону Дюлонга и Пти
)
значение теплоемкости соответствует
закону Дюлонга и Пти
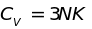 ;
а при низких температурах (
;
а при низких температурах (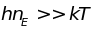 )
)
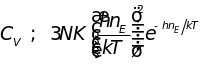
уменьшается
экспоненциально. Хотя модель Эйнштейна
сильно упрощает реальную ситуацию в
кристалле, формула (4.19) хорошо описывает
экспериментальные данные. Серьезные
расхождения наблюдаются лишь при очень
низких температурах. В эксперименте,
уменьшение теплоемкости происходит по
закону
 .
.