
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
3.8. Третье начало термодинамики (теорема Нернста)
В 1906 г. на основе большого числа исследований многообразных свойств при температурах, близких к абсолютному нулю, В.Ф.Г. Нернстом был установлен новый закон – третье начало термодинамики. Согласно этому закону в авторской формулировке, изменение энтропии во всех процессах при абсолютном нуле равно нулю. Иными словами энтропия есть абсолютная постоянная, не зависящая ни от объема, ни от давления. Более узкой была формулировка М. Планка: энтропия идеально образованных кристаллов при абсолютном нуле равна нулю.
Этот закон особенно
нуждается в статистическом обосновании,
так как он, во-первых, не подкреплен
таким богатым экспериментальным
материалом, как первое и второе начала,
а во-вторых, существуют системы, свойства
которых не удовлетворяют третьему
началу. Рассмотрим произвольную
макроскопическую систему в состоянии
статистического равновесия
с энергией
при весьма низких температурах. Пусть
её возможные энергетические уровни
образуют последовательность
 ,
,
,
…, где
– наименьшая возможная энергия
(нормальный уровень), а
,
,
... – возбужденные энергетические
уровни. Считаем, что система удовлетворяет
каноническому распределению Гиббса
(1.59), и запишем её функцию состояния при
заданных
,
и
(1.60):
,
,
,
…, где
– наименьшая возможная энергия
(нормальный уровень), а
,
,
... – возбужденные энергетические
уровни. Считаем, что система удовлетворяет
каноническому распределению Гиббса
(1.59), и запишем её функцию состояния при
заданных
,
и
(1.60):

где
 .
Уровни энергии быстро сближаются с
ростом возбуждения так, что уже при
малых энергиях возбуждения расстояние
между уровнями ничтожно мало. Если
температура системы очень низка, а
именно:
.
Уровни энергии быстро сближаются с
ростом возбуждения так, что уже при
малых энергиях возбуждения расстояние
между уровнями ничтожно мало. Если
температура системы очень низка, а
именно:
 ,
то тепловые возбуждения недостаточны
для того, чтобы система могла попасть
в состояние
,
она должна находится в состоянии с
наименьшей энергией
.
Эти условия определяют функцию состояний
и свободную энергию
,
то тепловые возбуждения недостаточны
для того, чтобы система могла попасть
в состояние
,
она должна находится в состоянии с
наименьшей энергией
.
Эти условия определяют функцию состояний
и свободную энергию
 ;
;
 .
.
Здесь
не зависит от температуры и является
внутренней энергией равновесной системы
 .
Отсюда находим энтропию
.
Отсюда находим энтропию

Поскольку энергия системы точно определена, то тем самым заданы состояние системы и кратность вырождения. Поэтому энтропия при стремлении температуры системы к нулю является постоянной величиной:
 . (3.69.а)
. (3.69.а)
Это и есть содержание
третьего начала термодинамики. Если
кратность вырождения нормального уровня
равна единице
 ,
то приходим к формулировке Планка
,
то приходим к формулировке Планка
 (3.69.б)
(3.69.б)
Теорема Нернста
является следствием квантовой статистики,
где существенное значение имеет
дискретность состояний. Энергия
невырожденной системы меняется
непрерывным образом, и даже в весьма
малом интервале энергий
 существует изменяющееся бесконечно
большое число возможных состояний
.
Поэтому энтропия не может быть постоянной
при любой как угодно низкой (но конечной)
температуре. Однако при температуре,
близкой к абсолютному нулю, практически
все системы становятся вырожденными.
По этой причине третье начало термодинамики
рассматривается как общий закон для
любых равновесных систем безотносительно
к их агрегатному состоянию. Формула
(3.69) справедлива в равной мере для
твердых, жидких или газообразных веществ.
существует изменяющееся бесконечно
большое число возможных состояний
.
Поэтому энтропия не может быть постоянной
при любой как угодно низкой (но конечной)
температуре. Однако при температуре,
близкой к абсолютному нулю, практически
все системы становятся вырожденными.
По этой причине третье начало термодинамики
рассматривается как общий закон для
любых равновесных систем безотносительно
к их агрегатному состоянию. Формула
(3.69) справедлива в равной мере для
твердых, жидких или газообразных веществ.
В жидкой фазе вблизи абсолютного нуля существует только гелий II. Все обычные газы при достаточном давлении конденсируются задолго до тех температур, при которых энтропия стремится к нулю. Существуют, однако, системы, которые можно условно считать газообразными при , это прежде всего электронный газ в металле. Все же обычные вещества при достаточно низкой температуре переходят в твердое состояние.
Из
теоремы Нернста следует, что любые
теплоемкости системы ( ),
коэффициент объемного расширения (
),
коэффициент объемного расширения ( ),
термический коэффициент давления (
),
термический коэффициент давления (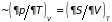 )
обращаются в нуль.
)
обращаются в нуль.
Часто
третье начало термодинамики формулируют
как недостижимость абсолютного нуля.
Представим себе цикл Карно, у которого
холодильник имеет температуру
 °К,
и тогда, согласно (3.69),
°К,
и тогда, согласно (3.69),
 .
Для такой обратимой машины полное
изменение энтропии в цикле равнялось
бы её изменению на участке изотермического
(
.
Для такой обратимой машины полное
изменение энтропии в цикле равнялось
бы её изменению на участке изотермического
( )
подвода тепла (первый этап)
)
подвода тепла (первый этап)

Но,
с другой стороны, в связи с обратимостью
процесса суммарное изменение
 .
Возникшее противоречие (
.
Возникшее противоречие ( )
доказывает недостижимость нулевой
изотермы
°К.
Данное положение, конечно, не запрещает
приближаться к
)
доказывает недостижимость нулевой
изотермы
°К.
Данное положение, конечно, не запрещает
приближаться к
 °К
сколь угодно близко. Следствия из теоремы
Нернста относятся к непосредственно
измеряемым величинам. Действительно,
для ряда веществ при
(алмаз,
,
°К
сколь угодно близко. Следствия из теоремы
Нернста относятся к непосредственно
измеряемым величинам. Действительно,
для ряда веществ при
(алмаз,
,
 и др.) экспериментальные результаты
полностью подтвердили выводы теории.
Однако, для большей части тел энтропия
оказывается не равной нулю (или константе)
при очень низких температурах. К ним
относятся аморфные тела, сплавы, а также
ряд химических соединений:
,
и др.) экспериментальные результаты
полностью подтвердили выводы теории.
Однако, для большей части тел энтропия
оказывается не равной нулю (или константе)
при очень низких температурах. К ним
относятся аморфные тела, сплавы, а также
ряд химических соединений:
,
 ,
и
т.д. Объясняется это тем, что подобные
системы при весьма низких температурах
не являются равновесными. Из-за малости
тепловой энергии возбуждения (большого
времени релаксации) в них происходит
очень длительный процесс, приближающий
их к состоянию равновесия (метастабильное
состояние).
,
и
т.д. Объясняется это тем, что подобные
системы при весьма низких температурах
не являются равновесными. Из-за малости
тепловой энергии возбуждения (большого
времени релаксации) в них происходит
очень длительный процесс, приближающий
их к состоянию равновесия (метастабильное
состояние).
