2.5. Столкновение молекул между собой

Выделим две молекулы идеального газа с массами и и скоростями и . Вопрос о столкновении этих молекул связан с характером их относительного движения. В механике показывается, что движение двух частиц можно всегда разложить на движение в пространстве общего центра тяжести и их относительное движение. Из определения скоростей относительного и абсолютного (центра тяжести двух молекул) движения, а именно:

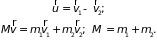
Находим зависимость и кинетическую энергию

(2.17)

где – приведенная масса. Первое слагаемое определяет энергию движения центра тяжести, а второе – энергию относительного движения. Относительное движение происходит так, как если бы одна из молекул была неподвижна, а вторая имела массу, равную приведенной .

Вероятность того, что одна молекула имеет скорость , а вторая – , равна произведению вероятностей простых событий, т.е.

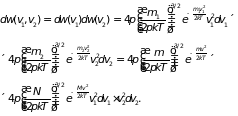
Перейдем в фазовом пространстве от переменных к переменным :

,

где учтено, что модуль якобиана преобразования равен . Искомая вероятность распадается на произведение и

(2.18)

Для упрощения считаем, что газ состоит из одинаковых молекул, . Используя указанное распределение, найдем среднюю скорость относительного движения

, (2.19)

которая оказывается в раза больше средней скорости теплового движения молекул газа.

В дальнейшем предполагаем, что газ настолько разрежен, что молекулы сталкиваются попарно, а числом столкновений, при котором одновременно приходят в непосредственный контакт три и более молекул будем пренебрегать. Соударение двух молекул – сложный процесс, зависящий от природы и характера их взаимодействия. Если молекулы рассматривать как твердые шарики радиуса , взаимодействующие только при непосредственном контакте, то для соударения центры молекул должны были бы сблизиться на расстояние . Иными словами, соударения происходят в том случае, когда центры сталкивающихся молекул лежат в круге площадью . Эту площадь называют геометрическим сечением соударения. В реальных газах молекулы начинают взаимодействовать еще до непосредственного контакта, на расстояниях 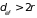. Это расстояние называют эффективным диаметром столкновения, а площадь круга – эффективным сечением соударения. При сильном взаимодействии между молекулами, эффективное соударение может, во-первых, существенно превышать геометрическое, во-вторых, зависеть от ряда факторов и прежде всего от относительной скорости сближающихся частиц. Будем считать, что все молекулы газа неподвижны, кроме одной, которая двигается со скоростью . Она проходит в единицу времени путь , вырезая в пространстве цилиндр объемом (рис. 2.5). При этом она испытывает столкновения со всеми неподвижными молекулами, находящимися в этом цилиндре. Их количество и определяет число соударений:

	, где – общая плотность молекул газа. Полное число соударений, испытываемых молекулой в единицу времени, вычисляется путем интегрирования этого выражения по всем возможным значениям :
Рис. 2.5.

Если сечение не зависит от относительной скорости, то с учетом (2.18) и (2.19) имеем

, (2.20)

. (2.21)

Это и есть число столкновений, испытываемое молекулой в 1 сек. Оно растет с увеличением температуры, плотности газа, размерами молекул и уменьшением их массы.