
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
2.2. Распределение Максвелла
Отдельно выделенная молекула идеального газа в данный момент времени находится в каком-то состоянии, которое характеризуется ее положением в пространстве, импульсом (скоростью, энергией). Через весьма короткое время в результате взаимодействия с другими молекулами она перейдет в другое состояние. Поэтому состояние одной молекулы из большой их совокупности не характеризует состояние всего газа. По этой же причине нет необходимости следить за последовательным изменением состояния отдельной молекулы с течением времени.
Задача сводится
к нахождению вероятности
 того, что одна произвольно выделенная
молекула из их совокупности в равновесном
идеальном газе попадает в некоторое
-е
состояние. Исходя из определения
идеального газа мы имеем: 1) наличие
макроскопической системы (термостата)
– газа, окружающего молекулу (подсистему);
2) слабое взаимодействие между молекулой
и термостатом. Эти условия характеризуют
ансамбль, подчиняющийся каноническому
распределению Гиббса.
того, что одна произвольно выделенная
молекула из их совокупности в равновесном
идеальном газе попадает в некоторое
-е
состояние. Исходя из определения
идеального газа мы имеем: 1) наличие
макроскопической системы (термостата)
– газа, окружающего молекулу (подсистему);
2) слабое взаимодействие между молекулой
и термостатом. Эти условия характеризуют
ансамбль, подчиняющийся каноническому
распределению Гиббса.
Элемент фазового
объема в
–пространстве
(шестимерном)
 в декартовой и сферической системах
координат соответственно равен
в декартовой и сферической системах
координат соответственно равен
 ,
,
 ,
,
а кинетическая энергия молекулы (в отсутствии внешнего поля) есть
 . (2.2)
. (2.2)
Подстановка этих
выражений в распределение Гиббса
определяет вероятность для молекулы
находится в объеме
и иметь энергию (импульс) в интервале
от
 до
(
до
( ):
):
 , (2.3)
, (2.3)
где
 .
Представление искомой вероятности в
виде произведения сомножителей
.
Представление искомой вероятности в
виде произведения сомножителей
 и
и
 свидетельствует о независимости импульса
(скорости) молекулы от ее положения в
пространстве и о независимости проекций
импульса (скоростей).
свидетельствует о независимости импульса
(скорости) молекулы от ее положения в
пространстве и о независимости проекций
импульса (скоростей).
В кинетической
теории газа принято считать, что проекции
импульса (скорости) могут принимать
значения от
 до
до
 .
В этом приближении интегралы в знаменателе
(2.3) оказываются равными
.
В этом приближении интегралы в знаменателе
(2.3) оказываются равными
 ,
,
 .
.
Подстановка их в
исходное равенство позволяет найти
вероятности того, что молекула имеет
как проекции, так и абсолютное значение
скорости, импульса ( )
и кинетическую энергию
)
и кинетическую энергию
 :
:
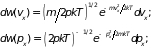 (2.4)
(2.4)
 (2.5)
(2.5)
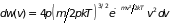 ; (2.6)
; (2.6)
 . (2.7)
. (2.7)
Формулы получили название распределение Максвелла. Здесь модуль статистической температуры заменен на . Правомерность замены обоснована в следующем разделе. Знание указанных вероятностей дает возможность определить плотность числа молекул, обладающих соответствующими параметром:
 , (2.8)
, (2.8)
где
– общая плотность молекул,
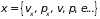 .
.
2.3. Столкновения молекул со стенкой сосуда. Давление
При движении в замкнутом сосуде молекула газа, приближаясь к стенке, со стороны ее молекул испытывает весьма сильное отталкивание и отражается внутрь сосуда. Можно считать, что отражение молекулы от стенки сосуда происходит совершенно упруго, т.е. компонента скорости, перпендикулярная плоскости стенки, при отражении меняет знак.
Выделим в стенке
сосуда площадью
 ,
перпендикулярную оси
.
Тогда при отражении от нее молекула,
имевшая компоненты скорости
,
перпендикулярную оси
.
Тогда при отражении от нее молекула,
имевшая компоненты скорости
 ,
приобретает компоненты скорости –
,
т.е. происходит изменение проекции
импульса на оси
от значения
,
приобретает компоненты скорости –
,
т.е. происходит изменение проекции
импульса на оси
от значения
 до значения
до значения
 .
Это изменение импульса
.
Это изменение импульса
 передается отражающей стенке. Таким
образом, столкновения молекул со стенкой
приводит к появлению силы, действующей
на поверхность сосуда. Силу, действующую
на единицу поверхности стенки со стороны
всех молекул газа, отождествляют с
макроскопическим давлением. Такое
утверждение, являющееся по сути основой
кинетической теории газов, казалось в
свое время радикальным. Однако сейчас
оно представляется естественным и
очевидным.
передается отражающей стенке. Таким
образом, столкновения молекул со стенкой
приводит к появлению силы, действующей
на поверхность сосуда. Силу, действующую
на единицу поверхности стенки со стороны
всех молекул газа, отождествляют с
макроскопическим давлением. Такое
утверждение, являющееся по сути основой
кинетической теории газов, казалось в
свое время радикальным. Однако сейчас
оно представляется естественным и
очевидным.
Для определения
давления нужно вычислить полное изменение
количества движения молекул газа,
испытывающих отражение от единицы
поверхности сосуда в единицу времени.
Очевидно, оно равно изменению импульса
в одном соударении со стенкой (
),
умноженному на полное число ударов в 1
сек на 1 см2 поверхности. В единицу
времени поверхности стенки будут
достигать все молекулы, находящиеся от
нее на расстоянии, меньшем или равным
 .
На 1 см2 поверхности за 1 сек попадают
все молекулы, находящиеся в цилиндре
высотой
с основанием 1 см2 (Рис. 2.1). В его
объеме
(см3) находится
.
На 1 см2 поверхности за 1 сек попадают
все молекулы, находящиеся в цилиндре
высотой
с основанием 1 см2 (Рис. 2.1). В его
объеме
(см3) находится
 молекул, компонента скорости которых
лежат между
и
молекул, компонента скорости которых
лежат между
и
 ;
;
 и
и
 ;
;
 и
и
 .
Поверхности стенок достигают все
молекулы, находящиеся в указанном
цилиндре, независимо от значения
компонент скорости
и
.
Здесь не учитываются столкновения
молекул между собой. Однако, молекулы,
не достигающие стенки из-за соударений,
передают свой импульс молекулам,
долетающим до стенки.
.
Поверхности стенок достигают все
молекулы, находящиеся в указанном
цилиндре, независимо от значения
компонент скорости
и
.
Здесь не учитываются столкновения
молекул между собой. Однако, молекулы,
не достигающие стенки из-за соударений,
передают свой импульс молекулам,
долетающим до стенки.


Рис. 2.1.
Число молекул с
проекцией скорости
 ,
которые за 1 сек достигают поверхности
стенки и общий импульс, передаваемый
ими, равны
,
которые за 1 сек достигают поверхности
стенки и общий импульс, передаваемый
ими, равны
 .
.
 .
.
Для вычисления
полного импульса проинтегрируем
последнее выражение по всем возможным
значениям компоненты скорости
от
 до
до
 :
:
 .
.
Отрицательные проекции скорости в расчет не берутся, т.к. эти молекулы движутся в противоположном направлении и не передают своего импульса стенке. Вычисленная таким образом величина есть сила, действующая на единицу площади, т.е. давление.
Сопоставление
(2.9) с уравнением состояния одного моля
(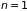 )
разреженного газа (2.1.а), полученным
опытным путем, определяет модуль
статистического распределения Гиббса
через абсолютную температуру
)
разреженного газа (2.1.а), полученным
опытным путем, определяет модуль
статистического распределения Гиббса
через абсолютную температуру
. (2.10)
