2.1. Нахождение корней характеристического уравнения систем

автоматического регулирования методом Берстоу

В разделах 1.1-1.3 был осуществлен вывод передаточной функции системы автоматического регулирования (САР) по ее структурной схеме, как зависимости от передаточной функции звеньев системы , где n – число сигналов системы.

Так как W_i является функцией комплексного переменного p, то можно перейти к представлению в виде отношения двух полиномов:

, (2.1)

где ;

(обычно ) (см. разд. 1.6, 1.7).

Так как главная передаточная функция САР

, (2.2)

где X(p) и Y(p) – изображения по Лапласу соответственно входной и выходной величин

; [24],

то для входного единичного ступенчатого воздействия :

,

. (2.3)

Окончательно для изображения выходной величины получим:

, (2.4)

где

Для аналитического получения переходного процесса в системе сначала нужно найти корни знаменателя (характеристического уравнения САР) . Один корень , а остальные n корней являются корнями полинома .Одним из методов нахождения любых (действительных или комплексно-сопряженных) корней полинома произвольной степени является численный метод Берстоу [8].

Сущность метода заключается в следующем. Из исходного полинома выделяется приведенный квадратный трехчлен. Если корни квадратного трехчлена являются корнями исходного полинома , то должно делиться на без остатка [8].

Продемонстрируем деление исходного полинома на полином :

…………………………

Таким образом, исходный полином представляется как

, (2.5)

где

(2.6)

Деление без остатка означает, что коэффициенты и должны быть равны нулю. Как видно из формулы (2.6) коэффициенты и являются функциями коэффициентов трехчлена r, q и коэффициентов исходного полинома :

;

.

Так как коэффициенты исходного полинома в общем случае неизвестны, то необходимо исследовать зависимость , .

Для нахождения корней методом Берстоу необходимо выбрать начальное приближение для коэффициентов трехчлена r и q. Затем значения коэффициентов r и q уточняем с помощью коррекции

. (2.7)

Требуется, чтобы остаточные члены и обращались в ноль в процессе вычисления. Если эти функции разложить в ряд Тейлора в окрестности точки , то получим:

(2.8)

Если предположить, что при уточнении r и q остаточные члены близки к нулю, то левые части этих уравнений обратятся в нуль. Тогда, решая (2.8) относительно и и пренебрегая членами более высоких порядков, получим:

(2.9)

и являются функциями , которые в свою очередь зависят от r и q. Поэтому необходимо получить последовательность частных производных , продифференцировав коэффициенты в формуле (2.6) по r и q. Получим:

Производные ис-пользуются для коррекции коэффициентов по формулам (2.7), (2.9). Вычисления коэффициентов r и q по выражениям (2.7), (2.9), (2.10), (2.11) ведутся до тех пор, пока полученные значения коэффициентов и не будут равны нулю с некоторой точностью :

(2.12)

Это означает, что корни трехчлена являются с некоторой точностью корнями исходного полинома .

После нахождения пары корней

, (2.13)

трехчлен исключается из , и процедура повторяется для полинома степени , являющегося результатом деления в формуле (2.5):

. (2.14)

Если порядок полинома меньше или равен двум, то вычисление корней заканчивается, а оставшиеся корень или два корня находят из решения линейного или квадратного уравнения. В результате получим все корни полинома .

В главе 1 по заданной структурной схеме САР находится ее передаточная функция Ф(p) и затем при подстановке в нее звеньев получается выражение для передаточной функции Ф(р) в виде отношения двух полиномов.

Рассмотрим пример нахождения корней знаменателя (характеристического уравнения САР) методом Берстоу для

.

Разделим числитель и знаменатель на 14,4 и получим передаточную функцию Ф(р):

.

Тогда характеристическое уравнение имеет вид:

Найдем корни полученного полинома. Для этого разделим данный полином на квадратный трехчлен .

где

Найдем частные производные коэффициентов , по r и q:

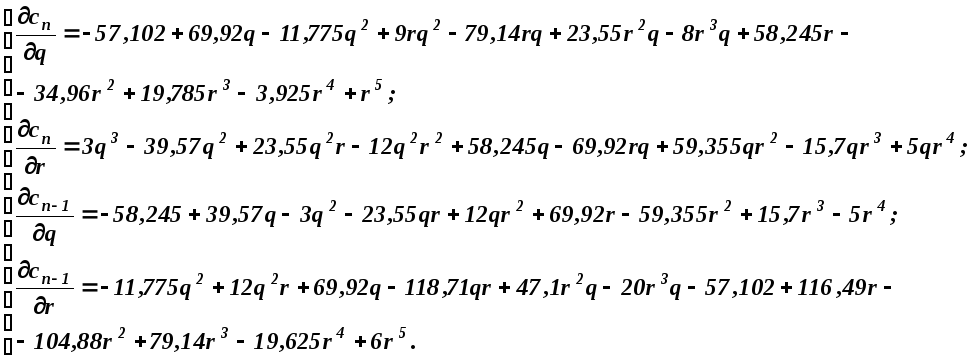
Далее осуществляется последовательность шагов поиска, причем на 1-ом шаге берутся нулевые значения коэффициентов трехчлена r и q. В дальнейшем dr и dq будут рассчитываться по формулам (2.9).

Таблица 2.1

Нахождение первой пары корней знаменателя Ф(p)

Шаг	r	q	Cn-1	Cn	dCn-1/dq	dCn-1/dr	dCn/dq	dCn/dr	dr	dq
1-й	0	0	24,429	3,583	-58,245	-57,102	-57,102	0,000	0,364	0,063
2-й	0,364	0,063	7,559	1,181	-37,962	-23,119	-36,930	2,382	0,248	0,048
3-й	0,612	0,111	2,104	0,38	-31,541	-8,102	-27,405	3,492	0,138	0,031
4-й	0,7495	0,142	0,557	0,124	-30,138	-0,363	-22,951	4,283	0,066	0,018
5-й	0,815	0,16	0,127	0,034	-29,941	3,459	-20,949	4,784	0,023	0,007
6-й	0,838	0,167	0,016	0,005	-29,936	4,841	-20,257	4,991	0,004	0,001
7-й	0,842	0,168	0,00	0,0001	-29,937	5,053	-20,152	5,024	0,00	310-5
8-й	0,842	0,168	0,00	710-8	-29,937	5,058	-20,150	5,025	0,00	110-8
9-й	0,842	0,168	0,00	210-14	-29,937	5,058	-20,150	5,025	0,00	510-15
10-й	0,842	0,168	0,00	710-16	-29,937	5,058	-20,150	5,025	0,00	0,00

Отсюда видно, что r = 0,842; q = 0,168. Таким образом, квадратный трехчлен есть . Тогда корни: ; .

Подставив r и q в выражения для с₁, с_2, с_3, с_4, с_5, получим полином пятого порядка: р⁵ + 3,083р⁴ + 17,021р³ + 20,11р² + 38,455р + 21,347.

Разделим полином полученный от первого деления: р⁵ + 3,083р⁴ + 17,021р³ + +20,11р² + 38,455р + 21,347 на квадратный трехчлен и получим полином третьего порядка р³ + с₁р² + с₂р + с₃, где

Найдем частные производные коэффициентов , по r и q:

Далее осуществляется последовательность шагов поиска, причем на 1-ом шаге берутся нулевые значения коэффициентов трехчлена r и q. В дальнейшем dr и dq будут рассчитываться по формулам (2.9).

Таблица 2.2

Нахождение второй пары корней знаменателя Ф(p)

Шаг	r	q	Cn-1	Cn	dCn-1/dq	dCn-1/dr	dCn/dq	dCn/dr	dr	dq
1-й	0	0	38,455	21,347	-17,021	-13,944	-20,11	0,000	1,462	1,062
2-й	1,462	1,062	26,193	22,917	-12,296	19,246	1,648	13,052	-1,69	-0,516
3-й	-0,229	0,545	34,142	9,216	-17,497	-21,509	-20,313	9,542	0,881	0,868
4-й	0,653	1,413	13,730	10,717	-11,448	-0,085	-5,011	16,178	-0,29	1,201
5-й	0,363	2,615	0,418	0,085	-9,951	-8,315	-1,967	26,017	0,00	0,042
6-й	0,362	2,657	0,001	0,004	-9,867	-8,408	-1,769	26,214	0,00	0,0002
7-й	0,362	2,657	-0,001	-110-7	-9,867	-8,410	-1,768	26,216	0,00	0,00

Отсюда видно, что q = 2,657, r = 0,362, а корни уравнения будут равны .

Подставив r и q в выражения для с₁, с_2, с_3, получим полином третьего порядка: р³ + 2,721р² + 13,379р + 8,035.

Для нахождения следующей пары корней разделим полученный полином на квадратный трехчлен и получим полином первого порядка р + с₁, где

Найдем частные производные коэффициентов , по r и q:

Далее осуществляется последовательность шагов поиска, причем на 1-ом шаге берутся нулевые значения коэффициентов трехчлена r и q. В дальнейшем dr и dq будут рассчитываться по формулам (2.9).

Таблица 2.3

Нахождение третьей пары корней знаменателя Ф(p)

Шаг	r	q	Cn-1	Cn	dCn-1/dq	dCn-1/dr	dCn/dq	dCn/dr	dr	dq
1-й	0	0	13,379	8,035	-1	-2,721	-2,721	0,000	3,832	2,953
2-й	3,832	2,953	14,680	11,314	-1	4,942	1,111	2,953	-3,272	-1,489
3-й	0,56	1,465	10,704	4,87	-1	-1,601	-2,161	1,464	3,708	4,766
4-й	4,268	6,230	13,750	17,673	-1	5,815	1,547	6,230	-2,558	-1,123
5-й	1,710	5,108	6,542	2,872	-1	0,699	-1,011	5,108	0,85	7,137
6-й	2,560	12,244	0,723	6,068	-1	2,399	-0,161	12,244	-0,502	-0,481
7-й	2,059	11,763	0,252	0,242	-1	1,396	-0,663	11,763	-0,007	0,242
8-й	2,052	12,005	0,00	-0,002	-1	1,382	-0,669	12,005	210-4	0,0003
9-й	2,052	12,005	0,00	410-8	-1	1,382	-0,669	12,005	0,00	210-8
10-й	2,052	12,005	0,00	0,00	-1	1,382	-0,669	12,005	0,00	0,00

Отсюда видно, что r = 2,052 и q = 12,005, а корни уравнения будут равны .

Подставив r и q в выражения для с₁, получим полином первого порядка: р+0,669, который имеет корень р₇ = -0,669.

В итоге корни полинома

будут равны:

р₁ = -0,324; р₂ = -0,518;

р₃ = -0,181 + 1,62j; р₄ = -0,181 - 1,62j;

р₅ = -1,026 + 3,31j; р₆ = -1,026 – 3,31j;

р₇ = -0,669.