Середні величини

Сутність і значення середніх величин

Середні величини у статистиці служать узагальнюючими мірами варіюючих ознак у статистичній сукупності. Статистичні показники, обчислені як середні величини, характеризують рівень ознаки в розрахунку на одиницю сукупності.

Середня величина відбиває типові розміри ознаки, характеризує якісні особливості явищ у кількісному вираженні.

Середні величини оцінюють однією величиною значення досліджуваної ознаки для всіх одиниць якісно однорідної сукупності.

Середня величина - величина абстрактна, оскільки характеризує значення абстрактної одиниці, і тому, відірвана від структури сукупності.

Середня величина визначається на основі індивідуальних значень і для кінцевої величини об’єктів.

При проведенні масового спостереження досліджуються великі за чисельністю сукупності. Отримані масові статистичні дані узагальнюються у вигляді ряду розподілу. Характер розподілу, частота повторення кожної ознаки впливають на середню, яка обчислюється за формулою для згрупованих даних і називається середньою зваженою. Частоти (ваги) показують повторюваність даного значення ознаки.

Використання кожного виду середніх залежить:

1. від характеру індивідуальних значень ознаки;

2. від характеру алгебраїчного зв’язку між індивідуальними значеннями ознаки та її загальним обсягом (сума, добуток, степінь і т. п.). Цей зв’язок – визначальна властивість сукупності, яка відображена логічною формулою осереднюваної ознаки.

Види середніх величин.

1. Середня арифметична () являє собою відношення загального обсягу значень ознаки до обсягу сукупності. Використовується для осереднення прямих значень ознаки шляхом підсумовування. Застосовується при вивченні закономірностей розподілу.

Середня арифметична проста (незважена) дорівнює сумі окремих значень ознаки, діленої на число цих значень: 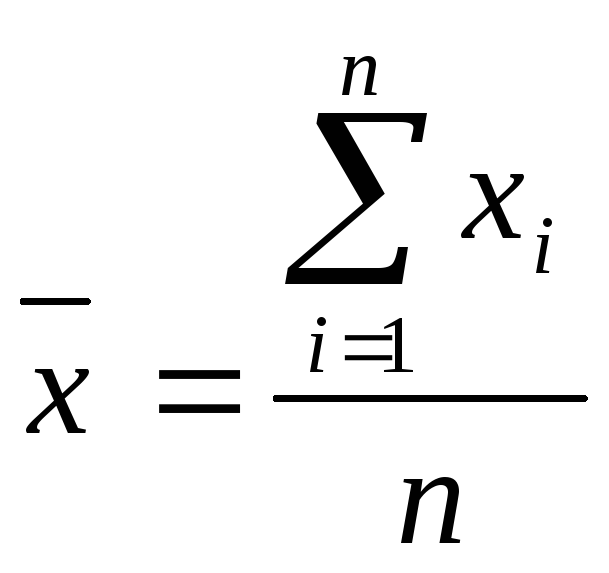, де x_i – значення ознаки i–ї одиниці сукупності; n – кількість спостережень (обсяг сукупності).

Проста середня арифметична застосовується у випадках, коли наявні окремі значення ознаки (тобто статистичні дані не згруповані).

Якщо статистичні дані представлені у вигляді рядів або розподілу (згруповані), тоді середня обчислюється як середня арифметична зважена:

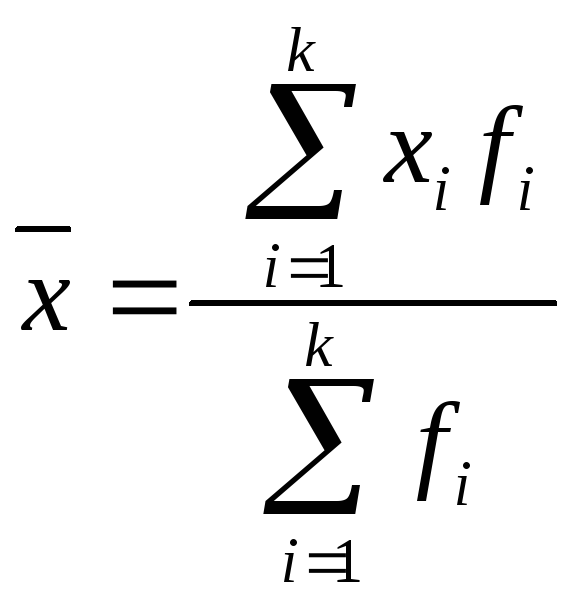- де f_і – абсолютна частота прояву ознаки x_i (статистична вага).

Властивості середньої арифметичної

Середня арифметична величина володіє рядом властивостей, що дозволяють прискорити розрахунок.

1. Вона не змінюється, якщо ваги усіх варіантів помножити або розділити на одне і те саме число.

2. Якщо всі значення ознаки однакові, тоді середня дорівнює цій же величині.

3. Середні суми або різниці дорівнюють сумі або різниці середніх:

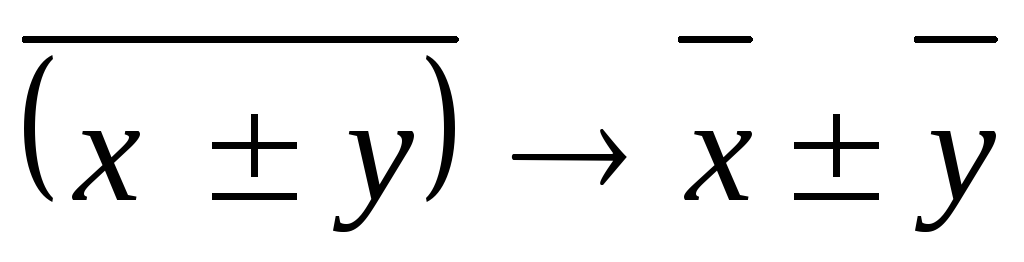
4. Якщо з усіх значень x_i відняти постійну величину А, то середня зменшується на це значення.

5. Якщо всі значення зменшити в d раз (x_i/d), то середня зменшиться в d раз.

6. Сума відхилень значення ознаки дорівнює 0.

7. Сума квадратів відхилень

2. Середня гармонійна визначається як величина обернена до середньої арифметичної з обернених величин. Використовується для осереднення обернених індивідуальних значень ознак шляхом підсумовування. Застосовується у випадках, коли осереднювала ознака є відношенням між логічно пов’язаними величинами, і чисельник дробу логічної формули відомий з наявних даних, а знаменник – ні.

Для не згрупованих даних розраховують середню гармонійну просту:

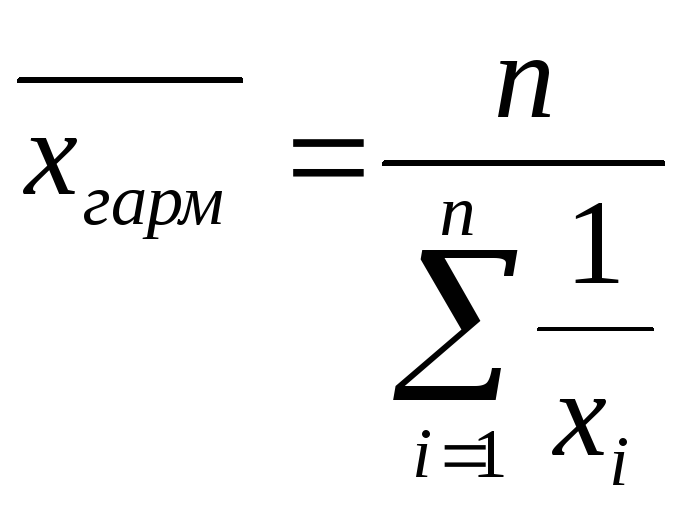
Якщо статистичні дані представлені у вигляді рядів або розподілу (згруповані), тоді середня обчислюється як середня гармонійна зважена:

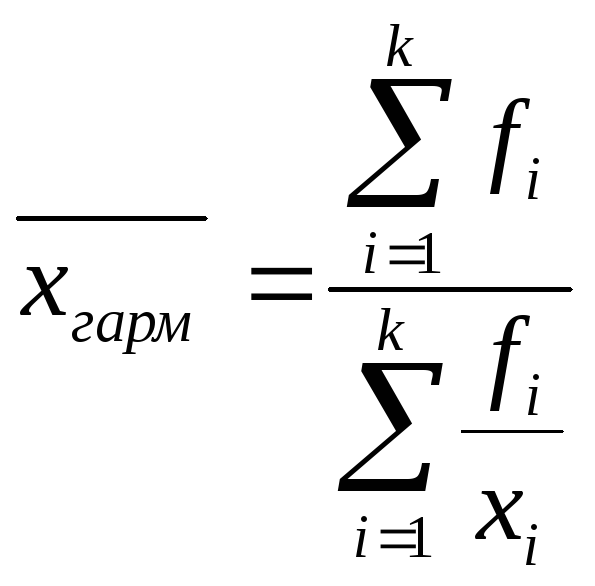- де сумарне значення ознаки.

3. Середня геометрична обчислюється як корінь n-го ступеню з добутку n множників. Використовується тоді, коли визначальна властивість сукупності формується як добуток індивідуальних значень ознаки. Найчастіше застосовується при дослідженні інтенсивності розвитку: обчисленні середньої частки відносних змін (середні темпи зростання, приросту) та побудові індексів.

- проста, для не згрупованих даних;

- зважена, для згрупованих даних, де ∑n_i = n часовий інтервал.

Поняття степеневої середньої, формула розрахунку.

Степенева середня - це така величина, що розрахована за індивідуальними значеннями ознаки, піднесеними у ступінь К, і приведена до лінійних розмірів:

Залежно від ступеню К середня може бути гармонійною (К = -1), арифметичною (К = 1), геометричною (К = 0), квадратичною (К = 2), кубічною (К = 3), біквадратичною (К = 4). Кожна середня має визначені властивості і має свою сферу застосування.

Якщо для одного і того ж самого первинного ряду обчислити різні степеневі середні, то чим більший показник степені К, тим більше абсолютне значення середньої:

Це правило мажорантности степеневих середніх.

4. Порядкові середні

Порядкові середні розраховуються у ряді розподілу, впорядкованому за зростанням або зменшенням значення ознаки.

Модою (x_Mo) називається варіант значення ознаки, який найчастіше зустрічається в сукупності, або те значення ознаки, що відповідає максимальній точці теоретичної кривої розподілу.

В дискретному ряді мода - це варіант із найбільшою частотою. В інтервальному варіаційному ряді мода приблизно дорівнює центральному варіанту так називаного модального інтервалу. Її значення оцінюється за допомогою формули апроксимації (наближення):

,

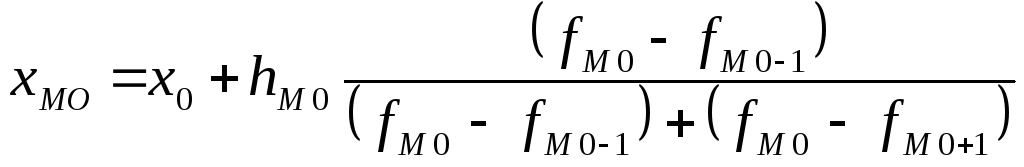де х₀ - нижня межа модального інтервалу;

h_M0 - ширина модального інтервалу;

f_M0 - абсолютна частота модального інтервалу;

f_M0-1 - абсолютна частота інтервалу перед модальним;

f_M0+1 - абсолютна частота інтервалу наступного за модальним.

Квантилі – це значення ознаки, які поділяють впорядкований ряд на певну кількість рівних частин. Наприклад:

• медіана – на 2 частини;

• терцилі – на 3 частини;

• квартилі – на 4 частини;

• квінтилі – на 5 частин;

• децилі – на 10 частин;

• процентилі – на 100 частин.

Медіана (x_Me) - це величина ознаки, що поділяє чисельність впорядкованого варіаційного ряду на 2 рівні частини. Одна частина значення варіюючої ознаки менша за медіану, а інша частина - більша. Для впорядкованого ряду з непарним числом членів медіаною є варіанта, розташована в центрі ряду, а у випадку з парним числом членів медіаною буде середня арифметична з двох суміжних центральних варіант.

В інтервальному варіаційному ряді порядок знаходження медіани наступний:

а) впорядковуємо індивідуальні значення ознаки за збільшенням (зменшенням) значення ознаки – за ранжиром;

б) визначаємо для даного ряду значення кумулятивної функції для частот, тобто нагромаджені частоти для кожного інтервалу значень;

в) за даними про нагромаджені частоти знаходимо медіанний інтервал.

Медіана поділяє чисельність ряду навпіл, отже, вона знаходиться в тому інтервалі, в якому значення кумулятивної функції складає половину або більше половини всієї суми частот, а значення кумулятивної функції для попереднього інтервалу менше половини чисельності сукупності.

Якщо припускати, що всередині медіанного інтервалу наростання або зменшення досліджуваної ознаки відбувається рівномірно, тоді формула апроксимації для медіани в інтервальному ряді розподілу буде мати наступний вигляд:

,

де х₀ - нижня межа медіанного інтервалу;

h_me - ширина медіанного інтервалу;

Σf/2 - полусума частот ряду (обсягу ряду);

F_Mе-1 – сума частот всіх інтервалів перед медіанним;

f_Mе - частота медіанного інтервалу.

Квартилі (Q) - це значення ознаки, що поділяють впорядкований ряд на 4 рівні частини. Розрізняють нижній квартиль Q1, медіану Ме і верхній квартиль Q3. Нижній та верхній квартилі розраховують за формулами:

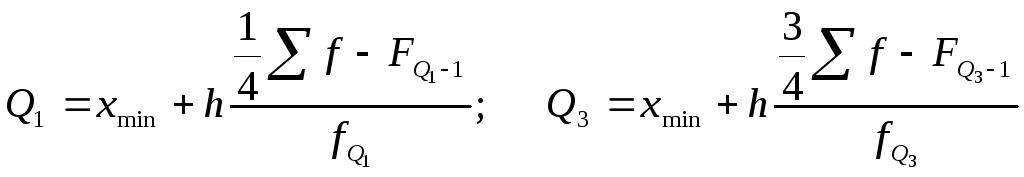
де x_min - мінімальні межі квартильних інтервалів;

h - ширина інтервалу ряду розподілу;

; - суми частот всіх інтервалів перед квартильним;

f_Q1; f_Q3 - частоти квартильних інтервалів.

Децилі (D) – варіанти, які поділяють впорядкований ряд на 10 рівних частин. Так, перший та другий децилі можна обчислити за формулами:

,

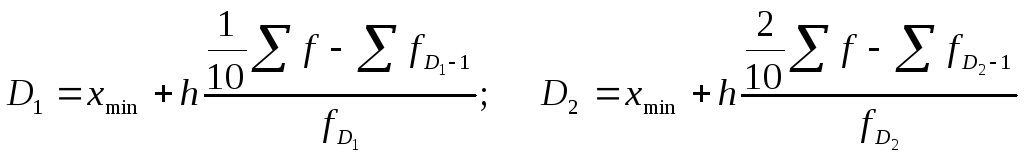де x_min - мінімальні межі децильних інтервалів;

h - ширина інтервалу ряду розподілу;

; - суми частот всіх інтервалів перед децильним;

; - частоти децильних інтервалів.