2. Симметричная форма злп на максимум имеет вид (4.3):

Симметричная форма задачи на минимум имеет вид (4.4):

Если все Bi ≥ 0, то задача (4.3) обычно имеет следующий экономический смысл: − Xj объемы производства j-го вида продукции, − Ci цены или прибыль единицы продукции, − Аij нормативы затрат i-го вида ресурса на производство единицы j-го вида продукции, − Bi имеющийся запас i-го вида ресурса. Надо определить план производства продукции Х* = (Х*1, Х*2, …, Х*n), который дает максимальную выручку или прибыль, при заданных ограничениях на имеющиеся ресурсы. Ограничения, на которых в оптимальном плане достигнуто равенство, соответствуют дефицитным ресурсам, остальные ресурсы называются недефицитными.

3. Каноническая форма злп представлена ниже (4.5 :

Из линейной алгебры известно, что количество линейно независимых уравнений не может быть больше числа неизвестных. Поэтому в (4.5) можно считать, что n ≥ m.

Определение. Если в ограничении задачи (4.5) есть переменная с коэффициентом, равным единице, отсутствующая в других ограничениях, то она называется базисной, остальные переменные ограничения называются свободными. Если базисные переменные есть во всех ограничениях, то такая форма ЗЛП называется канонической с базисными переменными. Каноническая форма с базисными переменными является исходной для решения задачи симплексным алгоритмом.

Опорным планом называется любой вектор Х = (Х1, Х2, …, Хn), удовлетворяющий условиям (4.5) и имеющий не более чем m ненулевых компонент. Если в канонической форме все bi ≥ 0, то задача (4.5) имеет опорный план, в котором базисные переменные равны bi, а остальные (свободные) переменные равны 0. Такой план называется начальным опорным планом.

Балансовой называется переменная, которая добавляется или вычитается из левой части неравенства для получения равенства. В задачах (4.3), (4.4) балансовые переменные будут базисными. Любая форма ЗЛП приводится к канонической форме с помощью следующих преобразований:

• замена переменной, которая принимает произвольные значения, на разность двух новых положительных переменных;

• введение балансовых переменных.

Искусственная переменная вводится, когда в канонической форме ЗЛП в ограничении нет базисной переменной. В этом случае целевая функция изменяется путем вычитания искусственной переменной с коэффициентом М в задаче на максимум и путем прибавления – в задаче на минимум. Коэффициент М считается большим положительным числом. При вводе искусственных переменных и корректировке целевой функции измененная задача называется М-задачей.

Пример 4.1. Пусть задача ЛП имеет вид (4.6):

Чтобы привести ее к канонической форме, сделаем подстановку а в неравенства введем балансовые переменные x4,x5 и искусственную переменную x6 . Тогда М-задача для (4.6) будет иметь вид (4.7):

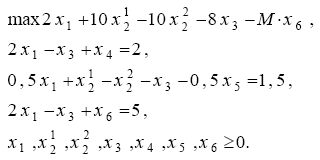
3. Геометрическая интерпретация и основные свойства задачи лп. Графическое решение задачи .

Решения задачи – планы – наборы из 2-х чисел х₁ и х₂, которые можно интерпретировать как точки двухмерного пространства.

Каждое ограничение системы представляет собой полуплоскость (выпуклое множество).

Выпуклым называется множество, которое вместе с любыми своими точками х₁ и х₂ содержит и все точки отрезка х₁х₂, т.е точки опр-ся из ур-ия:

х₁+λх₁+(1-λ)х₂

Полуплоскости пересекаются, образуя при этом прямую, отрезок, выпуклый многоугольник, неограниченную выпуклую многоугольную область, пустое множество, единственную точку.

Геометрич. интерпретацией целевой ф-ии явл. семейство параллельных прямых – линий уровня (линий постоянного значения целевой ф-ии). Они получаются путем подстановки вместо f(x) некот. чисел.

Вектор-градиент состоит из частных производных ф-ий по переменным, показывает направление наискорейшего возрастания целевой ф-ии.

ОДЗ –многоуг. область планов (решений).

Решить задачу с геометрической точки зрения – значит найти точку х₁* и х₂* (* - знак оптимальности) ОДЗ через которую проходит прямая семейства линий ур-ия, соответствующая наиб.(наим.) значению целевой ф-ии.

Порядок решения задачи ЛП графическим способом:

1. Построить ОДЗ.

2. Построить вектор-градиент.

3. Провести перпендикулярно вектору-градиенту линию ур-ия f=0.

4. переместить линию ур-ия f=0 в градиентном направлении так, чтобы она коснулась ОДЗ в крайнем положении.

Макс. или мин. достигается в вершинах. В ходе решения могут получиться след. результаты:

1. Оптим. план единственный, т.е. ОДЗ и линия уровня в разрешающем положении имеют 1 общую точку.

2. Оптим. планов бесконечное множество, в разрешающем положении линия уровня проходит через грань ОДЗ

3. Задача не имеет решений ОДЗ=Ø.