2.Основные виды записи злп.

Общей задачей линейного программирования (ОЗЛП) называют задачу

(1.24)

при ограничениях:

(i=1,..,m₁) (1.25)

(i=m₁+1,..,m₂) (1.26)

(i=m₂+1,…,m) (1.27)

x_j≥0 (j=1,..,n₁) (1.28)

x_j – произвольные (j=n₁+1,…,n) (1.29)

где c_j, a_ij, b_i – заданные действительные числа; (1.24) – целевая функция; (1.25) – (1.29) – ограничения; х=(x₁;…;x_n) план задачи.

Симметричной формой записи ЗЛП называют задачу

(1.30)

(i=1,..,m) (1.31)

x_j≥0 (j=1,..,n) (1.32)

или задачу

(1.33)

(i=1,..,m) (1.34)

x_j≥0 (j=1,..,n) (1.35)

В экономической практике задача (1.30) – (1.32) (или (1.33) – (1.35)) встречается наиболее часто.

Канонической формой записи ЗЛП называют задачу

(1.30)

(i=1,..,m) (1.31)

x_j≥0 (j=1,..,n) (1.32)

Рассмотрим еще два употребительных вида записи – матричную и векторную. В модель (1.36) – (1.38) введем обозначения:

C=[c₁ c₂ … c_n], , ,

где C – матрица–строка; A – матрица системы управлений; X – матрица–столбец переменных; A₀ – матрица–столбец свободных членов.

Каноническая форма задачи примет вид:

max Z=[c₁ c₂ … c_n][x₁ x₂ … x_n]^T

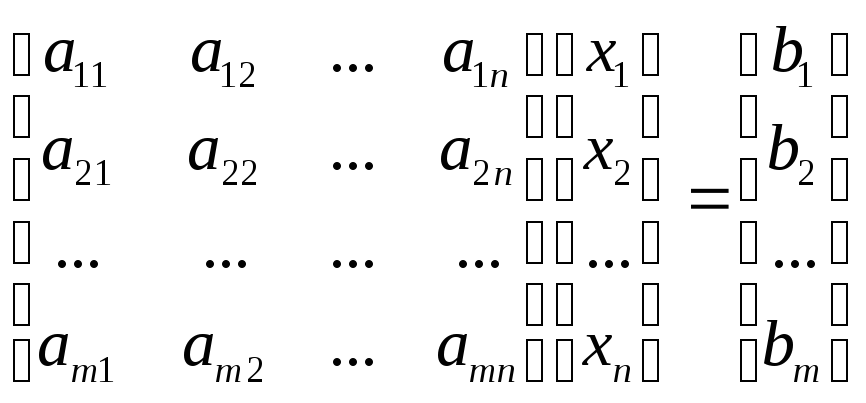, X≥0,

или

max Z=CX, AX=A₀, X≥0

Полезной является также векторная форма ЗЛП. Для столбцов матрицы A введем обозначения:

Тогда задача (1.36) – (1.38) в векторной форме записи примет вид:

max Z=cx;

A₁x₁+…+A_jx_j+…+A_nx_n=A₀, x≥0

где cx – скалярное произведение векторов c=(c₁;…;c_n) и x=(x₁;…;x_n).

2.Виды записи задачи лп. Способы преобразования.

ЗЛП в общей постановке имеет 3 формы: произвольную, симметричную и каноническую.

1. Произвольная форма злп имеет вид (4.2):

Выражение называется целевой функцией (или критерием) задачи. Величины (Х1, Х2, …, Хn) – переменные задачи. Система неравенств в задаче (4.2) определяет область допустимых значений (планов) задачи D, которая имеет форму выпуклого многогранника. Неравенства и равенства в задаче (4.2) называются ограничениями. Каждое неравенство определяет полупространство, а равенство – плоскость в пространстве переменных (Х1, Х2, …, Хn).

Решение задачи (4.2) называется оптимальным решением (или оптимальным планом) и обозначается как Х* = (Х*1, Х*2, …, Х*n). Оптимальные решения лежат на границе области D. Если область D ограничена, то задача ЛП имеет либо единственное, либо бесконечно много решений. Если решение единственно, то оно совпадает с одной из вершин многогранника D. Если градиент целевой функции c = (с1, с2, …, сn) коллинеарен градиенту одного из ограничений, то задача имеет бесконечно много решений, лежащих на данном ограничении. Если ограничения несовместны, или целевая функция неограниченна, то задача (4.2) не имеет решения. Если область области D не ограничена, то решение может существовать либо быть неограниченным. Всякая задача на минимум может быть сведена к задаче на максимум и наоборот, умножением целевой функции на –1. Оптимальный план задачи при этом не изменится, а значение целевой функции изменит знак. После решения надо снова изменить знак целевой функции.