8. Область неограниченна, но оптимальное решение существует

В случае, если в предыдущей задаче изменить тип критерия с максимизации на минимизацию прибыли, то решение будет существовать. Аналогично первой задаче можно получить ответ графическим способом: x₁=200[шт] x₂=200[шт] минимальная прибыль F=3600 руб.

9. Вырожденное опорное решение

Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным

С графической точки зрения решение является вырожденным, когда три или более полуплоскостей пересекаются в одной точке.

Рассмотрим на примере следующей задачи:

Для производства шариков для пейнтбола зимнего и летнего типа требуется соответственно по 5 г желатина, 2 и 3 мл краски на водной основе и 2 и 1 мл стабилизатора. На складе производителя имеется: 15 кг желатина, 10 л краски и 7л стабилизатора. Стоимость шарика зимнего типа – 2руб, летнего типа 1,5 руб. Необходимо найти, сколько произвести шариков каждого типа (x₁ и x₂). Для достижения максимальной прибыли.

Запишем ограничения:

Ограничение по желатину:

x₁[шт]*5[г]+ x₂[шт]*5[г]≤15000[г] (14)

Ограничение по краске:

x₁[шт]*2[мл]+ x₂[шт]*3[мл]≤8000[мл] (15)

Ограничение по стабилизатору:

x₁[шт]*2[мл]+ x₂[шт]*1[мл] ≤4000[мл] (16)

Критерий запишется так:

F=2[руб]*x₁[шт]+ 1.5[руб]*x₂[шт]→max (17)

На графике Рис. 5 видно, что три полуплоскости (14), (15), (16) пересекаются в одной точке. Решив систему уравнений:

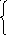
x₁*5+ x₂*5=15000

x₁*2+ x₂*3=8000 (18)

x₁*2+ x₂*1=4000

можно найти ее координаты x₁=1000, x₂=2000.

Как видно из графика, она же будет и оптимальной точкой, значит оптимальная прибыль

F=2[руб]*1000[шт]+ 1.5[руб]*2000[шт]=5000[руб]

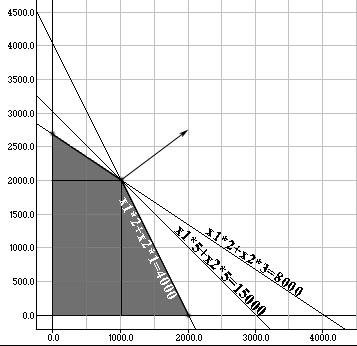
Рис. 5. Вырожденный случай.

Пересечение трех полуплоскостей в одной точке

тр

Приведем ограничения к каноническому виду и посмотрим, как это будет выглядеть в симплекс таблице:

1. Первый опорный план x⁽¹⁾=(0,0,15000,8000,4000)

Cb	БП	x1	x2	x3	x4	x5	b
0 0 0	x3 x4 x5	5 2 2	5 3 1	1 0 0	0 1 0	0 0 1	15000 8000 4000
	ƒ	-2	-1.5	0	0	0	0

Получаем первую замену x₅ на x₁

2. Второй опорный план x⁽²⁾=(2000,0,5000,4000,0)

Cb	БП	x1	x2	x3	x4	x5	b
0 0 2	x3 x4 x1	0 0 1	2.5 2 0.5	1 0 0	0 1 0	-2.5 -1 0.5	5000 4000 2000
	ƒ	0	-0.5	0	0	1	4000

Определяем вторую замену x₃ на x₂

3. Третий опорный план x⁽³⁾=(1000,2000,0,0,0)

Cb	БП	x1	x2	x3	x4	x5	b
1.5 0 2	x2 x4 x1	0 0 1	1 0 0	0.4 -0.8 -0.2	0 1 0	-1 1 1	2000 0 1000
	ƒ	0	0	0.2	0	0.5	5000

Получили оптимальное решение (все коэффициенты критерия ≥0). Число положительных компонент меньше числа ограничений. Значит, признак вырожденности решения в симплекс таблице: в столбце свободных членов b есть нулевой элемент.

Строго говоря, при вырожденном базисном решении не всегда можно получить ответ. В случае, если данное вырожденное базисное решение не является оптимальным, решение задачи может зациклиться на замене одних и тех же переменных.