
- •Производная
- •1.1. Определение производной
- •Правила дифференцирования
- •1.2. Дифференцирование неявных функций
- •1.3. Логарифмическое дифференцирование
- •1.4. Производные высших порядков
- •1.5. Дифференцирование функции, заданной параметрически
- •1.6. Уравнение касательной к нормали
- •2. Исследование поведения функций
- •2.1. Возрастание и убывание функции
- •2.2. Максимум и минимум функций
- •2.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.4. Асимптоты
- •3. Наибольшее и наименьшее значения функции на отрезке
- •4. Правило лопиталя
- •Задания к контрольной работе № 2
- •Первообразная и неопределенный интеграл
- •Свойства интегралов
- •Методы интегрирования
- •1. Непосредственное интегрирование
- •2. Метод замены переменной (подстановки)
- •3. Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •2. Правильные и неправильные рациональные дроби
- •3. Разложение правильной дроби
- •4. Нахождение коэффициентов
- •5. Правило интегрирования рациональных дробей
- •Интегрирование некоторых иррациональностей
- •Интегрирование тригонометрических выражений
- •Определенный и несобственный интегралы, их вычисление
- •Геометрические приложения определенного интеграла
- •Задачи к контрольной работе № 3
Интегрирование некоторых иррациональностей
Основным методом решения интегралов от иррациональных выражений является метод замены переменной.
Цель замены – преобразовать данное иррациональное выражение к рациональной дроби.
-
 сводится
к
сводится
к
 ,
,
предварительно необходимо выделить полный квадрат под знаком корня, сделать замену и проинтегрировать по таблице интегралов, 10 и 12.
Пример 29.

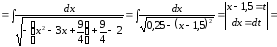
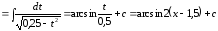 .
.
2.
 .
.
-
Сделать в числителе производную подкоренного выражения.
-
Разбить на два интеграла, один из которых степенной, а другой вида (1).
Пример 30.


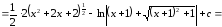
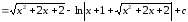 .
.
3.
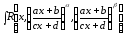 подстановка
подстановка
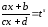 ,
,
 – наименьший
общий знаменатель дробей
– наименьший
общий знаменатель дробей
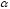 и
и
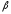 .
.
Пример
31.
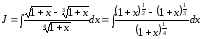
Здесь
роль
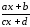 играет
играет
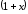 ,
,
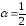 ;
;
 ;
;
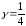 ,
наименьший общий знаменатель этих
дробей
,
наименьший общий знаменатель этих
дробей
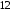 ,
следовательно, подстановка
,
следовательно, подстановка
 ,
вычислим
,
вычислим
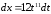
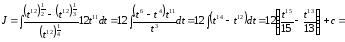
 .
.
4.
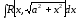 ,
, 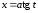 ;
;
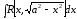 ,
, 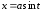 ;
;
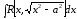 ,
, 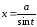 .
.
5.
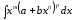 – дифференциальный бином интегрируется
в трех случаях:
– дифференциальный бином интегрируется
в трех случаях:
1)
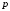 – целое,
– целое,
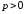 – интегрируется непосредственно,
– интегрируется непосредственно,
 – подстановка
– подстановка
 ,
где
,
где
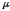 – общий знаменатель дробей
– общий знаменатель дробей
 и
и
 ;
;
2)
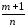 – целое (
– целое (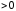 ,
,
 ,
,
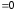 )
подстановка
)
подстановка
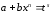 ,
где
,
где
 – знаменатель
– знаменатель
дроби
 ;
;
3)
 – целое (
– целое (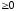 ,
,
 ,)
подстановка
,)
подстановка
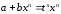 .
.
Пример
32.
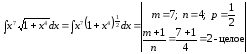

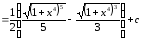 .
.
Интегрирование тригонометрических выражений
1.
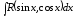 решается универсальной подстановкой
решается универсальной подстановкой
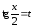 ,
,
 ,
, 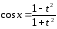 ;
;  .
.
Пример
33.

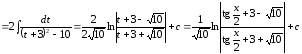 .
.
В некоторых случаях полезнее использовать подстановки, которые дают лучший результат, чем при использовании универсальной подстановки.
2.
Если в подынтегральном выражении при
замене
 на
на
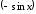 и
и
 на
на
 функция не меняет своего знака, т. е.
если
функция не меняет своего знака, т. е.
если
 ,
,
то
применяют подстановку
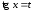 .
.
Пример
34.
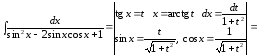
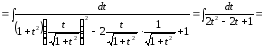
 .
.
3.
Если
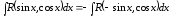 ,
т. е. при замене
,
т. е. при замене
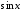 на
на
 подынтегральная функция меняет знак,
то подстановка
подынтегральная функция меняет знак,
то подстановка
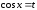 .
.
Пример
35.

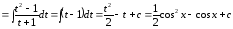 .
.
4.
Если
 ,
т. е. при замене
,
т. е. при замене
 на
на
 подынтегральная функция меняет знак,
то подстановка
подынтегральная функция меняет знак,
то подстановка
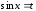 .
.
Пример
36.
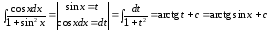 .
.
5.
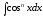 ; при
; при
 – четном,
– четном,
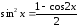 ;
;
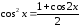
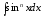 ; при
; при
 – нечетном по правилу 3 или 4.
– нечетном по правилу 3 или 4.
Пример
37.
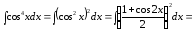
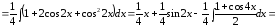
 .
.
Пример38.
 .
.
Пример
39.
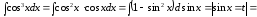
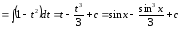 .
.
6.
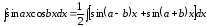 ,
,
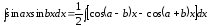 ,
,
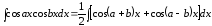 .
.
Пример40
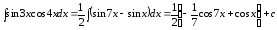 .
.
Определенный и несобственный интегралы, их вычисление
Если
1)
 и
и
 конечны;
конечны;
2)
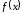 непрерывна на
непрерывна на
 и имеет первообразную
и имеет первообразную
 ,
то определенный интеграл выражается
конечным числом и может быть вычислен
по формуле Ньютона-Лейбница:
,
то определенный интеграл выражается
конечным числом и может быть вычислен
по формуле Ньютона-Лейбница:
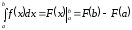 .
(21)
.
(21)
Пример
41.
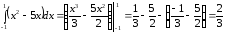 .
.
Интегралы
а)
 ; б)
; б)
 ; в)
; в)
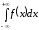
относятся
к несобственным интегралам I-го
рода, т. к. для них не выполнено условие
(1), а именно: один из пределов интегрирования
(случая а) и б) ) или оба (случай в)) не
являются конечными, а условие (2) выполнено.
Вычисление таких интегралов можно
проводить по формуле (21), при этом
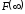 считается как предельное значение,
которое может быть конечным, бесконечным
или не иметь смысла.
считается как предельное значение,
которое может быть конечным, бесконечным
или не иметь смысла.
Пример
42.
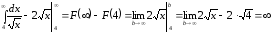 .
.
Пример
43.
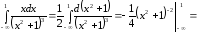
 .
.
Пример
44.
 .
.
Если в результате вычислений получили конечное число, то несобственный интеграл называется сходящимся (примеры 52, 53), в противном случае интеграл расходится (пример 51).
Те
интегралы
 ,
для которых не выполняется условие (2),
а условие (1) выполнено, относятся к
несобственным интегралам II-го
рода.
,
для которых не выполняется условие (2),
а условие (1) выполнено, относятся к
несобственным интегралам II-го
рода.
 имеет бесконечный разрыв в одной или
нескольких точках.
имеет бесконечный разрыв в одной или
нескольких точках.
Вычисление несобственных интегралов II-го рода и определение их сходимости или расходимости можно проводить по формуле Ньютона-Лейбница, определив точки бесконечного разрыва.
Пример
45.
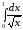 ;
;
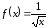 ;
эта функция имеет бесконечный разрыв
на
;
эта функция имеет бесконечный разрыв
на
 в точке
в точке
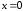 ,
т. к.
,
т. к.
 .
.
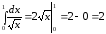 ,
интеграл сходится.
,
интеграл сходится.
Пример
46.
 ;
;
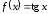 имеет бесконечный разрыв на
имеет бесконечный разрыв на
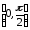 в точке
в точке
 ,
т. к.
,
т. к.
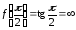 .
.
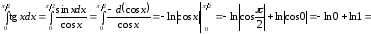
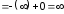 ,
интеграл расходится.
,
интеграл расходится.
Пример
47.
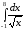 ;
;
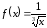 имеет бесконечный разрыв в точке
имеет бесконечный разрыв в точке
 ,
которая принадлежит
,
которая принадлежит
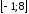 .
В этом случае данный интеграл разбиваем
на два интеграла точкой разрыва:
.
В этом случае данный интеграл разбиваем
на два интеграла точкой разрыва:
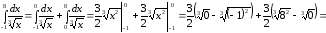
 ,
интеграл сходится.
,
интеграл сходится.
