2. Метод замены переменной (подстановки)

Для вычисления интеграла 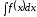сделаем замену , где 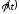выбирается так, чтобы после преобразований данного интеграла и новой переменной , получился интеграл, который берется непосредственно.

Предварительно находим 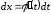, тогда

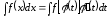. (18)

После нахождения первообразной необходимо вернуться к первоначальной переменной «».

Пример 7.

.

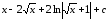Пример 8.

.

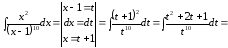
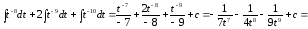
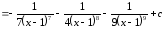Замечание. Следующие интегралы удобно решать указанной заменой:

, ; ;

, ; ;

, ; .

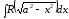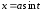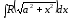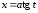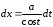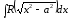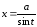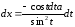Пример 9.

,

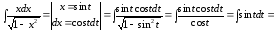
т. к. .

Формулой (18) часто пользуются справа налево:

, . (19)

При этой замене надо помнить, что в составе подынтегрального выражения должен быть дифференциал функции .

Такой метод называется подведением под знак дифференциала

. (19’)

При использовании этого метода можно воспользоваться таблицей дифференциалов.

Таблица дифференциалов

1. , – const, ,

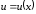2.

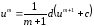
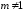
3.

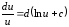
4. , , ,

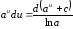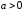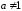5.

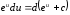
6.

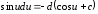
7.

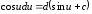
8.

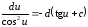
9.

10. ,

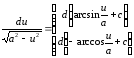11. ,

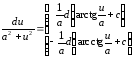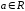
Пример 10. .

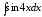Решение. Согласно таблице дифференциалов, 1, с. 7 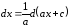, положим , , , .

.

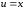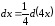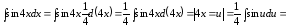
Пример 11. .

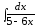Решение. По таблице дифференциалов, 1, с. 7 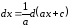, положим

, , , .

.

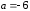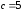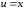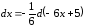Пример 12. – можно найти двумя способами:

1 способ.

;

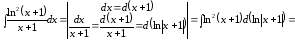
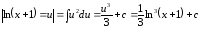2 способ. .

Пример 13. .

1 способ.

;

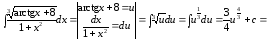
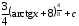2 способ.

.

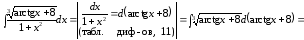
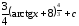Пример 14.

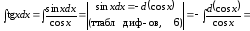
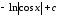. (табл. интегр., 3, ).

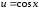3. Метод интегрирования по частям

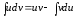(20)

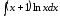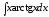Эта формула чаще всего применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функции, например, или , или .

– это все подынтегральное выражение, часть которого мы обозначаем за , а часть за . При этом:

1. за принимается функция, которая дифференцированием упрощается.

2. за 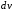– та часть, интеграл от которой известен или легко может быть взят.

3. в состав 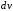обязательно входит .

В итоге верного выбора и и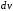нтеграл в (20) должен быть проще исходного.

Пример 15.

.

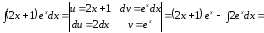
Замечание. Метод интегрирования по частям может применяться в одном примере несколько раз.

Замечание. Иногда повторное интегрирование по частям приводит к уравнению искомого интеграла , , 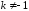если

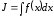, то получаем уравнение: , откуда

или .

Пример 16. – решить методом по частям, используя примечание. При верном решении должен получиться ответ:

.

Только по частям берутся интегралы:

а) , 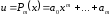многочлен 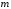-ой степени,

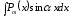, в частности одночлен

, ,

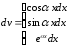б) , ,

,

, ,

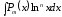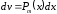в) , , ,

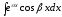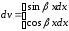, или .

Интегралы типа (в) интегрируются дважды по частям.

Пример 17.

.

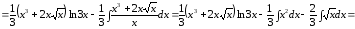
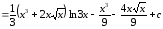Рассмотрим отдельные классы функций и способы их интегрирования.

Интегрирование рациональных дробей

1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:

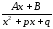1. , 2. , 3. , при ,

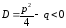4. 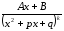, при (, , , , , ).

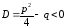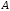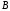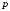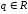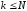При интегрировании дробей типа 1 – 2 достаточно ввести подстановку 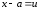, (или 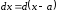), тогда

1. ;

2. , ().

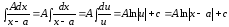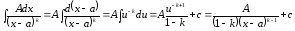Чтобы проинтегрировать дроби типа 3 – 4, необходимо выделить полный квадрат из квадратного трехчлена, затем свести интеграл к табличному.

Пример 18. .

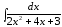Решение. Выделим полный квадрат из квадратного трехчлена:

.

=

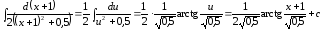
(табл. интегр., 11).

Замечание. При интегрировании дробей типа 3 – 4 можно воспользоваться справочником.