2. Правильные и неправильные рациональные дроби

Определение 13. Дробь 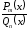называется рациональной, где 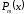, – многочлены -ой и -ой степеней.

Если 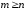, дробь неправильная.

Если 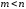, дробь правильная.

Неправильную дробь представляют в виде суммы целой части и правильной дроби. Операция выделения целой части может быть выполнена делением числителя на знаменатель.

Пример 19. Дробь неправильная (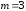, , 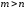). Выделим целую часть, разделив числитель на знаменатель.

.

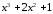
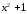
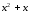
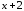
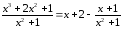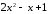
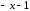
Пример 20. Дробь 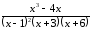правильная, т. к. , , .

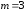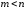Пример 21. Дробь неправильная (, , ).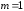

.

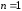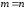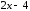
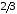
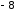
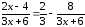3. Разложение правильной дроби

Теорема. Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей вида 1 – 4.

Пусть дробь правильная. Разложим знаменатель дроби на множители. Найдем его корни, т. е. значения , при которых знаменатель обращается в нуль. Тогда многочлен 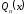разложится на множители:

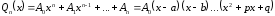, где

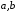– действительные корни многочлена. Множитель 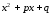не разложим на линейные множители, т. к. .

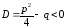Вид элементарной дроби и число их в разложении определяется корнями знаменателя данной дроби. Каждому множителю знаменателя соответствует определенного вида дробь. Укажем, какому множителю какая дробь соответствует:

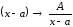
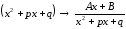, если .

,

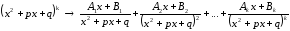если .

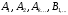– пока неизвестные коэффициенты.

Разложить на простейшие дроби.

Пример 22. .

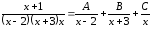Пример 23.

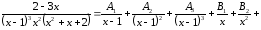
– не имеет действительных корней, т. к. .

Пример 24.

.

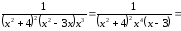
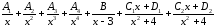Пример 25.

,

– не имеет действительных корней, т. к. .

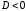4. Нахождение коэффициентов

I способ.

Пусть , , .

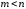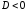Написанное равенство есть тождество, а поэтому:

а) приведя дроби к общему знаменателю, получим тождественные многочлены в числителях справа и слева;

б) приравняем числители;

в) а затем их коэффициенты при одинаковых степенях;

г) получим систему уравнений для определения коэффициентов.

Пример 26. Рассмотрим пример 31.

а) Приведем дробь к общему знаменателю:

.

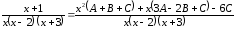б) Приравняем числители:

.

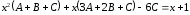в) Приравняем коэффициенты при одинаковых степенях:

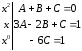(коэффициент при )

(нет коэффициента при )

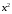(свободный член).

г) Решив систему, получим:

; ; .

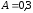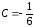Получили разложение

.

II способ.

Приравняем многочлены в числителях слева и справа, как в I способе:

д) Придадим частные значения, вычислим значения многочленов. Получим также систему с неизвестными коэффициентами.

В качестве значений удобно брать значения действительных корней знаменателя, лучше применять в случае, когда знаменатель имеет равные действительные корни.

Пример 27. ,

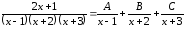а)

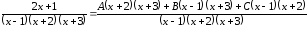
б)

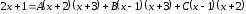
д)

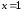
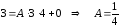
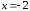
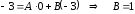
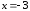
В итоге .

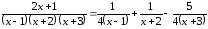III способ.

Комбинируют I и II способы.

5. Правило интегрирования рациональных дробей

Чтобы проинтегрировать рациональную дробь, необходимо:

1. Проверить, является ли эта дробь правильной. Если дробь неправильная, выделить целую часть, разделив числитель на знаменатель.

2. Правильную рациональную дробь разложить на сумму простейших дробей.

3. Найти неизвестные коэффициенты.

4. Проинтегрировать простейшие дроби.

Пример 28. .

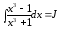Дробь 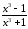неправильная,

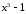
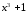
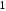
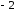
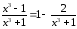
Дробь – правильная, разложим знаменатель дроби на множители:

,

.
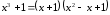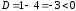
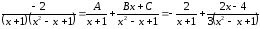
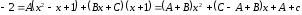
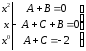
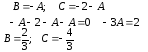
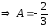
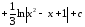