
- •Производная
- •1.1. Определение производной
- •Правила дифференцирования
- •1.2. Дифференцирование неявных функций
- •1.3. Логарифмическое дифференцирование
- •1.4. Производные высших порядков
- •1.5. Дифференцирование функции, заданной параметрически
- •1.6. Уравнение касательной к нормали
- •2. Исследование поведения функций
- •2.1. Возрастание и убывание функции
- •2.2. Максимум и минимум функций
- •2.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.4. Асимптоты
- •3. Наибольшее и наименьшее значения функции на отрезке
- •4. Правило лопиталя
- •Задания к контрольной работе № 2
- •Первообразная и неопределенный интеграл
- •Свойства интегралов
- •Методы интегрирования
- •1. Непосредственное интегрирование
- •2. Метод замены переменной (подстановки)
- •3. Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •2. Правильные и неправильные рациональные дроби
- •3. Разложение правильной дроби
- •4. Нахождение коэффициентов
- •5. Правило интегрирования рациональных дробей
- •Интегрирование некоторых иррациональностей
- •Интегрирование тригонометрических выражений
- •Определенный и несобственный интегралы, их вычисление
- •Геометрические приложения определенного интеграла
- •Задачи к контрольной работе № 3
1.5. Дифференцирование функции, заданной параметрически
Пусть
даны две функции
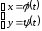 ,
(1)
,
(1)
где
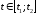 назовем параметром. Причем
назовем параметром. Причем
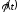 имеет обратную функцию
имеет обратную функцию
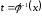 .
Тогда из (1)
.
Тогда из (1)
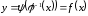 ,
т. е.
,
т. е.
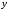 является функцией от
является функцией от
 .
Задание функции
.
Задание функции
 через
через
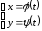 называется параметрическим.
называется параметрическим.
Если
функции
 ,
,
 имеют производные
имеют производные
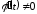 и
и
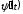 ,
то функция
,
то функция
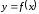 также имеет производную, вычисляемую
по формуле
также имеет производную, вычисляемую
по формуле
 .
(2)
.
(2)
Вторая производная вычисляется по формуле
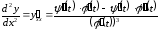 .
(3)
.
(3)
Пример
7. Функция
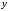 задана параметрически:
задана параметрически:
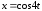 ,
,
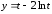 ,
,
 .
Найти
.
Найти
 и
и
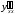 .
.
Решение.
Найдем
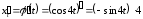
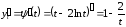 .
.
Тогда
по формуле (2)
 .
.
Для
вычисления
 найдем
найдем
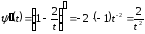 .
.
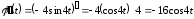 .
.
Подставим
в формулу (3):

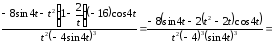
 .
.
1.6. Уравнение касательной к нормали
Касательной
к линии
 в точке
в точке
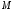 (рис. 1) называется прямая
(рис. 1) называется прямая
 ,
с которой стремится совпасть секущая
,
с которой стремится совпасть секущая
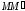 ,
когда точка
,
когда точка
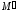 ,
оставаясь на
,
оставаясь на
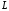 ,
стремится
,
стремится
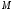 - будь то справа или слева.
- будь то справа или слева.
Если
линия
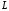 есть график функции
есть график функции
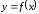 ,
то угловой коэффициент касательной
равен значению производной функции в
соответствующей точке.
,
то угловой коэффициент касательной
равен значению производной функции в
соответствующей точке.
Если
график не имеет касательной, функция
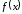 не имеет производной и наоборот.
не имеет производной и наоборот.
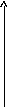



Рис. 1
Эти
видно из рис. 1. Угловой коэффициент
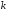 секущей равен
секущей равен
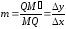 .
Если
.
Если
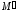 стремится к
стремится к
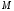 ,
то
,
то
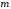 имеет пределом угловой коэффициент
имеет пределом угловой коэффициент
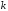 касательной. Значит,
касательной. Значит,
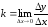 ,
т. е.
,
т. е.
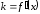 .
.
Уравнение
прямой, проходящей через данную точку
с данным угловым коэффициентом:
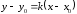 ,
значит уравнение касательной к кривой
,
значит уравнение касательной к кривой
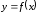 в точке
в точке
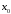
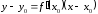 ,
где
,
где
 .
.
Нормалью
к кривой
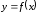 в точке
в точке
 называется прямая, перпендикулярная
касательной. Условие перпендикулярности
двух прямых:
называется прямая, перпендикулярная
касательной. Условие перпендикулярности
двух прямых:
 ,
значит уравнение нормали будет иметь
вид:
,
значит уравнение нормали будет иметь
вид:
 .
.
Пример
8. Составите
уравнение касательной и нормали к кривой
 в точке
в точке
 .
Сделать чертеж.
.
Сделать чертеж.
Решение.
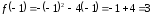
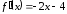 ,
, 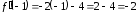 .
.
Уравнение
касательной:
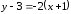
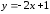 .
.
Уравнение
нормали:
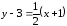 ;
;  .
.
Сделаем
чертеж.
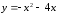 – парабола, ветви направлены вниз.
Вершина
– парабола, ветви направлены вниз.
Вершина
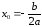 ,
,
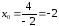 ,
,
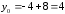 .
.
Точки
пересечения с осью
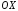 :
:




 ,
,
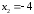

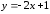

 0
1
0
1
 0 1
0 1
 1
-1
1
-1
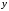 3,5 4
3,5 4
2. Исследование поведения функций
Изучение количественной стороны различных явлений природы приводит к установлению и изучению функциональной зависимости между участвующими в данном явлении величинами. Если такую функциональную зависимость можно выразить аналитически, то есть в виде одной или нескольких формул, то мы получаем возможность исследовать эту функциональную зависимость средствами математического анализа.
Установим общие приемы исследования поведения функции.
2.1. Возрастание и убывание функции
Дадим некоторые определения.
Определение.
Если функция
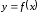 такова, что большему значению аргумента
такова, что большему значению аргумента
 соответствует большее значение функции,
то функция
соответствует большее значение функции,
то функция
 называется возрастающей.
Аналогичным образом определяется
убывающая функция.
называется возрастающей.
Аналогичным образом определяется
убывающая функция.
Пример
9. Функция
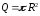 при
при
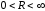 есть возрастающая функция, так как
большему значению
есть возрастающая функция, так как
большему значению
 соответствует большее значение
соответствует большее значение
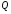 .
.
Применим понятие производной для исследования возрастания и убывания функции.
Теорема
1. Если функция
 ,
имеющая производную на отрезке
,
имеющая производную на отрезке
 ,
возрастает на этом отрезке, то ее
производная на отрезке
,
возрастает на этом отрезке, то ее
производная на отрезке
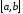 не отрицательна, то есть
не отрицательна, то есть
 .
.
Теорема
2. Если функция
 непрерывна на
непрерывна на
 и дифференцируема в промежутке
и дифференцируема в промежутке
 ,
причем
,
причем
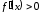 для
для
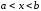 ,
то эта функция возрастает на отрезке
,
то эта функция возрастает на отрезке
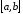 .
.
Геометрически:
если на
 функция
функция
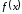 возрастает, то касательная к кривой
возрастает, то касательная к кривой
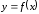 в каждой точке на этом отрезке образует
с осью
в каждой точке на этом отрезке образует
с осью
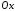 угол
угол
 :
:
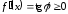 .
Если
.
Если
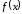 убывает на отрезке
убывает на отрезке
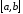 ,
то угол наклона касательной – тупой.
,
то угол наклона касательной – тупой.
