
- •Производная
- •1.1. Определение производной
- •Правила дифференцирования
- •1.2. Дифференцирование неявных функций
- •1.3. Логарифмическое дифференцирование
- •1.4. Производные высших порядков
- •1.5. Дифференцирование функции, заданной параметрически
- •1.6. Уравнение касательной к нормали
- •2. Исследование поведения функций
- •2.1. Возрастание и убывание функции
- •2.2. Максимум и минимум функций
- •2.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.4. Асимптоты
- •3. Наибольшее и наименьшее значения функции на отрезке
- •4. Правило лопиталя
- •Задания к контрольной работе № 2
- •Первообразная и неопределенный интеграл
- •Свойства интегралов
- •Методы интегрирования
- •1. Непосредственное интегрирование
- •2. Метод замены переменной (подстановки)
- •3. Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •2. Правильные и неправильные рациональные дроби
- •3. Разложение правильной дроби
- •4. Нахождение коэффициентов
- •5. Правило интегрирования рациональных дробей
- •Интегрирование некоторых иррациональностей
- •Интегрирование тригонометрических выражений
- •Определенный и несобственный интегралы, их вычисление
- •Геометрические приложения определенного интеграла
- •Задачи к контрольной работе № 3
Задания к контрольной работе № 2
I.
Найти производные
 данных функций:
данных функций:
1.
а)
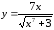 б)
б)
 в)
в)
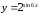
г)
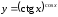 д)
д)

2.
а)
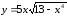 б)
б)
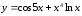 в)
в)
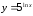
г)
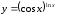 д)
д)

3.
а)
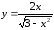 б)
б)
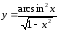 в)
в)
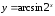
г)
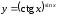 д)
д)
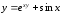
4.
а)
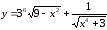 б)
б)
 в)
в)
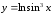
г)
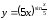 д)
д)

5.
а)
 б)
б)
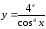 в)
в)
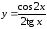
г)
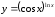 д)
д)

6.
а)
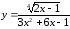 б)
б)
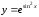 в)
в)

г)
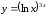 д)
д)

7.
а)
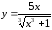 б)
б)
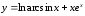 в)
в)
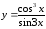
г)
 д)
д)

8.
а)
 б)
б)
 в)
в)
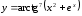
г)
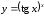 д)
д)

9.
а)
 б)
б)
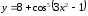 в)
в)

г)
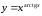 д)
д)

10.
а) б)
б)
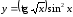 в)
в)
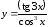
г)
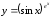 д)
д)
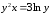
II.
Найти
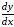 и
и
 :
:
11.
а)
 б)
б)
 ;
; 
12.
а)
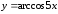 б)
б)
 ;
; 
13.
а)
 б)
б)
 ;
; 
14.
а)
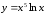 б)
б)
 ;
; 
15.
а)
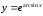 б)
б)
 ;
; 
16.
а)
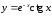 б)
б)
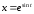 ;
; 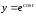
17.
а)
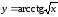 б)
б)
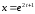 ;
; 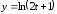
18.
а)
 б)
б)
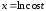 ;
; 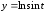
19.
а)
 б)
б)
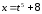 ;
; 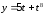
20.
а)
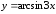 б)
б)
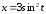 ;
; 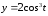
III.
Найти наибольшее и наименьшее значения
 на отрезке
на отрезке
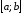 :
:
21.
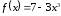
 26.
26.

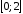
22.

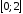 27.
27.


23.
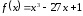
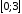 28.
28.

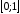
24.
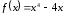
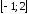 29.
29.
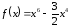

25.
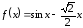
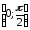 30.
30.


IV.
Исследовать методами дифференциального
исчисления функции
 ;
используя результаты исследования,
построить ее график:
;
используя результаты исследования,
построить ее график:
31.
а)
 36.
а)
36.
а)

32.
а)
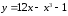 37.
а)
37.
а)
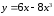
33.
а)
 38.
а)
38.
а)

34.
а)
 39.
а)
39.
а)
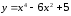
35.
а)
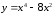 40.
а)
40.
а)

V.
Составить уравнения касательной и
нормали к кривой
 в точке
в точке
 .
Сделать чертеж.
.
Сделать чертеж.
41.
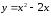 ,
, 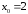 46.
46.
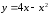 ,
, 
42.
 ,
, 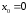 47.
47.
 ,
, 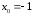
43.
 ,
, 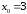 48.
48.
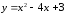 ,
, 
44.
 ,
,  49.
49.
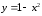 ,
, 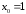
45.
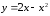 ,
,  50.
50.
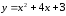 ,
, 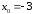
VI. Найти пределы функций по правилу Лопиталя:
51.
а)
 б)
б)
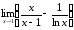
52.
а)
 б)
б)
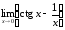
53.
а)
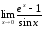 б)
б)
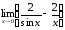
54.
а)
 б)
б)

55.
а)
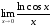 б)
б)

56.
а)
 б)
б)

57.
а)
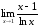 б)
б)

58.
а)
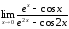 б)
б)

59.
а)
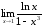 б)
б)

60.
а)
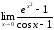 б)
б)

Интегрирование
Первообразная и неопределенный интеграл
Определение
1. Функция
 называется первообразной для
называется первообразной для
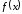 ,
если
,
если
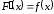 (15)
(15)
или
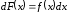 (16)
(16)
Пример
1.
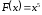 есть первообразная для
есть первообразная для
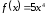 ,
так как
,
так как
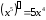 или
или
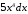 .
.
Пример
2.
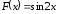 есть первообразная для
есть первообразная для
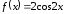 ,
так как
,
так как
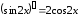 или
или
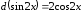 .
.
Всякая
непрерывная функция
 имеет бесчисленное первообразная,
которое отличаются друг друга на
постоянное число.
имеет бесчисленное первообразная,
которое отличаются друг друга на
постоянное число.
Так
в 11-м примере для
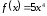 первообразной будут, кроме
первообразной будут, кроме
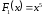 ,
,
 ,
,
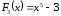 ,
,
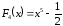 ,
и другие. Все они удовлетворяют условию
(15) и (16). Вообще в общем виде можно записать
первообразную в виде
,
и другие. Все они удовлетворяют условию
(15) и (16). Вообще в общем виде можно записать
первообразную в виде
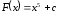 ,
где
,
где
 – произвольная постоянная. Действительно,
– произвольная постоянная. Действительно,

или
 .
.
Определение
2. Общее
выражение
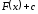 совокупности всех первообразных для
функции
совокупности всех первообразных для
функции
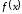 называется неопределенным интегралом
от этой функции и обозначается:
называется неопределенным интегралом
от этой функции и обозначается:
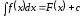 .
(17)
.
(17)
При
этом
 ,
где
,
где
 – подынтегральное
выражение,
– подынтегральное
выражение,
 – подынтегральная
функция.
– подынтегральная
функция.
Операцию нахождения неопределенного интеграла называют интегрированием.
Итак, интегрирование представляет собой операцию, обратную дифференцированию, поэтому каждой формуле дифференцирования (15) соответствуют формула интегрирования (17).
Пример
3.
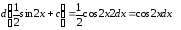
 ,
,
где
 – const.
– const.
Ниже приведена таблица основных интегралов. Каждую формулу можно проверить дифференцированием.
Таблица основных интегралов
1.
 (
( ,
,
 – const,
– const,
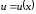 )
)
2.
 (для
любого
(для
любого
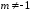 )
)
2.1.
 2.2.
2.2.
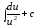
3.

4.
 (
( ,
,
 ,
,
 )
)
5.

6.
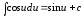
7.
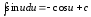
8.

9.
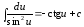 10.
10.
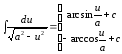 (
( )
)
11.
 (
(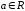 )
)
12.

13.
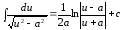
При интегрировании используются свойства интегралов.
Свойства интегралов
-

-
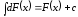 ,
в частности,
,
в частности,
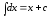
 ,
, 
-
 ,
где
,
где

-

Таблицу интегралов и свойства необходимо выучить наизусть.
Методы интегрирования
Существуют три способа интегрирования: непосредственное, заменой переменной и по частям.
1. Непосредственное интегрирование
Непосредственное интегрирование состоит в том, что подынтегральную функцию путем тождественных преобразований с использованием формул алгебры и тригонометрии, а также, используя свойства (3) и (4), сводят к табличным интегралам.
Рассмотрим несколько примеров.
Пример
4.
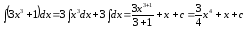 .
.
(Использованы
свойства 3, 4; табличный интеграл 2,
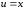 ).
).
Правильность ответа проверяем дифференцированием:
 .
.
Пример
5.

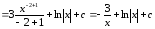 .
.
(Свойства 3, 4; табличные интегралы 2.2 и 3).
Пример
6.

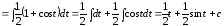 .
.
(Свойства 3,4; табличные интегралы 1 и 7).
