Лекция 3 Случайные величины и их характеристики

Внезапные отказы определяются случайными неблагоприятными сочетаниями нескольких факторов. Случайность связана с тем, что причины события остаются для нас скрытыми. Поэтому параметры надежности рассматриваются как случайные величины, которые могут принимать то или иное значение, неизвестное заранее. Случайные величины могут быть непрерывного или дискретного типа.

В теории надежности используются следующие характеристики случайных величин.

1. Функция распределения случайной величины х (функция вероятности)

Для каждого числа х в диапазоне изменения случайной величины Х существует определенная вероятность Р(Х < х), того, что Х не превосходит х. Эта зависимость F(x) = P(X < x) называется функцией распределения или функцией вероятности случайной величины Х. Функция F(x) является неубывающей функцией х (монотонно возрастающей для непрерывных процессов и ступенчато возрастающей для дискретных процессов).

В пределах изменения случайной величины Х функция F(x) изменяется от 0 до 1.

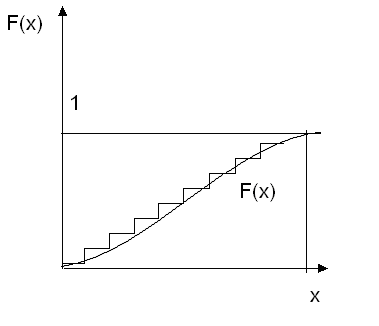
График функции распределения случайной величины

2. Плотность распределения.

Плотность распределения - производная от функции распределения по текущей переменной

Плотность распределения характеризует частоту повторений данного значения случайной величины. В задачах надежности она используется как плотность вероятности.

В ряде случаев достаточно характеризовать распределение случайной величины некоторыми числовыми величинами, характеризующими рассеяние случайной величины. Эти характеристики распределений используются в статистической трактовке (для обработки результатов наблюдений) и в вероятностной трактовке (для прогнозирования надежности).

3. Математическое ожидание

Математическое ожидание (среднее значение) m_х – основная и простейшая характеристика случайной величины Х. Значение математического ожидания, определяемого по результатам наблюдений как для дискретных, так и для непрерывных величин, называют оценкой математического ожидания или оценкой среднего значения х:

,

где N – общее число наблюдений; х_i – значение случайной величины. При достаточно большом значении N полагают, что

В вероятностных задачах математическое ожидание определяют в зависимости от плотности распределения f(x) (для непрерывных величин) или вероятности р_i появления значений х_i (для дискретных величин).

; .

4. Дисперсия случайной величины

Дисперсия – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Термин «дисперсия» означает рассеяние и характеризует разброс случайной величины.

Оценка дисперсии случайной величины – среднее значение квадрата разности между значениями случайной величины и ее средним значением:

Для непрерывных случайных величин:

Для дискретных случайных величин:

5. Среднее квадратичное отклонение

Дисперсия имеет размерность квадрата случайной величины. Характеристика рассеяния (дисперсия) имеет размерность случайной величины. Поэтому для удобства использования была введена характеристика - среднее квадратичное отклонение - корень квадратный из дисперсии:

.

6. Коэффициент вариации.

Для оценки рассеяния с помощью безразмерной (относительной) величины используют коэффициент вариации, равный отношению среднего квадратичного отклонения к математическому ожиданию:

.

7. Квантиль

Квантиль - значение случайной величины, соответствующее заданной вероятности.

8. Медиана

Медиана - квантиль, соответствующая вероятности 0,5.

Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.

9. Мода

Мода - наиболее вероятное значение случайной величины, т.е. значение, при котором плотность вероятности максимальна.

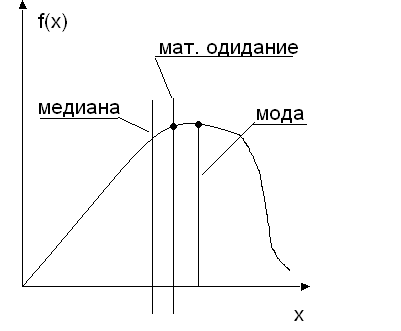
Общие сведения о законах распределения времени безотказной работы.

1. Распределение Вейбулла

Р′(t)=;

,

где - табулированная гамма – функция.

2.Экспоненциальное распределение

Экспоненциальное распределение – частный случай распределения Вейбулла :

; Р′(t)=;.

3. Распределение Релея

; ; ; ,

где С – параметр распределения.

4. Нормальное распределение

; ,

где дисперсия времени безотказной работы; среднее время безотказной работы.