
ms_lec
.pdfМОДЕЛЮВАННЯ СИСТЕМ
ЛЕКЦІЯ 14
ФРАКТАЛЬНИЙ АНАЛІЗ ЧАСОВИХ РЯДІВ
Дається визначення поняття фракталу, та його основних характеристик, таких як самоподібність та масштабованість. Розглянуто поняття фрактальної, метричної та топологічної розмірностей. Приведені методи фрактального аналізу часових рядів, зокрема метод розмірності мінімального покриття, метод нормованого розмаху, та обчислення показника Герста.
Особливістю математичного моделювання складних систем є те, що забезпечуючи вимоги, які ставляться до моделі, і в першу чергу досягнення максимальної відповідності, побудова математичної моделі вимагає принаймні спроби використати не лише знання її автора, але і ті знання, які існують і використовуються іншими дослідниками, які самі потребують і певного осмислення і глибокого опанування як підстави наукового обґрунтування даної моделі, її адекватності та ефективності.
З давніх часів вважалося, що вміння передбачати це доля мудреців, і разом з тим, передбачення – це одна з основних цілей науки. Розвиток математики істотно розширив можливості дослідників у проведенні наукового прогнозу. Виявилося, наприклад, що рух небесних тіл можна розраховувати, розв’язуючи диференціальні рівняння, які можуть бути досить складними, і для їх вирішення потрібно буде докласти чимало зусиль. Така робота захопила вчених на багато років і, здавалося, єдиною перешкодою будуть чисто математичні труднощі, які з часом будуть подолані.
Однак з розвитком науки виникло розуміння того, що не всі цілі, які стоять перед наукою – науковими дослідженнями можуть бути досягнуті чи реалізовані. Так, з появою термодинаміки стало зрозуміло, чому ніколи не побудують вічний двигун. Квантова механіка показала, що ми принципово позбавлені можливості виміряти з заздалегідь заданою точністю одночасно координату і імпульс елементарної частинки. На непереборні бар'єри вказала теорія відносності. По суті, розуміння нових обмежень стало ознакою фундаментальних теорій.
Важливе місце серед наукових досліджень останніх років займають роботи, пов'язані з передбачуваністю. Стимулом до таких досліджень стала робота американського метеоролога Е. Лоренца, опублікована в 1963 р. Лоренц поставив перед собою питання: чому за наявності потужних ЕОМ не можна дати надійний, досить довгостроковий прогноз погоди. Він запропонував просту модель, яка описувала динаміку атмосфери, і прорахував її на ЕОМ. Вивчаючи одне з численних рішень системи, Лоренц вивів на друк проміжні результати розрахунків у форматі «три знаки після десяткової коми» при точності представлення «шість знаків після коми» в пам'яті машини. Використовуючи потім ці проміжні дані в якості початкових для подальшого рахунку, Лоренц виявив, що після відповідного розрахунку результати кардинальним чином відрізнялися від тих, які були отримані без проміжного виведення значень на друк, тобто без відкидання трьох останніх знаків у проміжних результатах. Отримавши такий результат, Лоренц не відмахнувся від нього як від помилки обчислень, а поставився дуже серйозно. Отриманий результат – був виникненням хаотичних відхилень, що нагадували випадкові коливання, хоча модель Лоренца була цілком детермінованою, тобто в рівняннях її динаміки повністю були відсутні випадкові параметри.
121
Таким чином, в системі, де майбутнє однозначно визначається минулим, Лоренц виявив скінченний горизонт прогнозу. Це явище отримало назву детермінованого (динамічного ) хаосу.
Слідом за роботою Лоренца почалися інтенсивні дослідження даного явища. Виявилося, що хаотичним коливанням (явищам), які виникають згідно з регулярними законам, властивий не «безформний» хаос, а хаос з прихованим порядком. Цей порядок пов'язаний з поняттям фрактальної структури. І хоча в математиці подібні конструкції в тій чи іншій формі з'являлися більше ста років тому, у фізиці цінність подібних ідей була усвідомлена лише в 70-х роках ХХ століття.
Динамічний хаос і фрактальні структури властиві не тільки, як здавалося б на перший погляд, фізичним нелінійним системам. В даний час фракталам і хаосу присвячено багато книг і оглядів, велике число статей опубліковано в провідних наукових журналах світу з математики, фізики, хімії, біології, медицині, економіці та інших. Звичайно, фрактали присутні в багатьох структурах зовсім не пов'язаних з явищем динамічного хаосу, та й явище хаосу не завжди супроводжується фрактальним утворенням. Однак, говорячи про них разом, треба підкреслити, з одного боку, їх природний взаємозв'язок, а з іншого, відзначити одночасне підвищення інтересу до цих явищ.
Поняття фракталу стало новою математичною моделлю, що дає єдиний опис властивостей, які характерні для багатьох природних явищ. Цим пояснюється сучасна популярність фрактального підходу до аналізу різних об'єктів.
14.1. Самоподібність та фрактальна розмірність
Поняття фракталу ввів французький математик Бенуа Мандельброт, який є засновником фрактальної геометрії. Фрактальна геометрія інтенсивно розвивається, знаходячи широке застосування в найрізноманітніших областях наукового знання, де було запропоновано надзвичай багато визначень фракталів – від строго математичних до метафоричних. В одній з останніх робіт Мандельброт визначає фрактали як неправильні, шорсткі, пористі або роздроблені об'єкти, форма яких відтворюється в будь-якому масштабі, тобто за його визначенням «можна сказати, що форма цих об'єктів не змінюється від того, розглядаємо ми їх поблизу або здалеку», а це вказує на властивість фракталів, яку зазвичай називають масштабною інваріантністю.
Самоподібність фракталів. Основними властивостями фракталів, як математичних об’єктів, є їх самоподібність та розмірність. Самоподібність або масштабна інваріантність об’єкта полягає в тому, що такий об’єкт складається з частин, отриманих шляхом перетворення подібності цілого об’єкта. Іншими словами, структура фракталу в одному масштабі подібна до його структури в іншому, більшому масштабі. Проте властивість точної самоподібності характерна лише для регулярних фракталів. Природні фрактали завжди містять деякий елемент випадковості і хоча збільшена частина фракталу є неідентичною даному фрагменту, однак їхні статистичні характеристики збігаються. Формою кількісного вираження цієї подібності є фрактальна розмірність DF
Найпростішим прикладом масштабної інваріантності є самоподібність. Самоподібний об'єкт складається з частин, які утворюються шляхом перетворення подібності цілого об'єкта. При цьому перетворення подібності, тобто лінійне стиснення (редукція) об'єкта, може супроводжуватися перенесенням, відображенням (осьовою симетрією) або обертанням. У підсумку будь-яка мала частина самоподібного об'єкта, якщо її збільшити, може бути накладена на його велику частину або на об'єкт в цілому.
Один з найвідоміших в математиці самоподібних об'єктів це сніжинка Коха. Алгоритм її побудови полягає в послідовності кроків, проілюстрованих на рис. 1.
Зміст цього алгоритму в тому, що взявши за основу рівносторонній трикутник (тобто нульовий крок), кожну з його сторін ділять на три рівних відрізки. Середній відрізок кожної сторони використовується як основа побудови нових рівносторонніх трикутників, після чого основи нових трикутників відкидаються (це вважають 1-м кроком). Далі, кожну зі сторін утвореного багатокутника ділиться на три рівних відрізка і на середніх відрізках знову будують рівносторонні трикутники, після чого їх основи відкидаються (це 2-й крок). І так далі, до нескінченності.
122
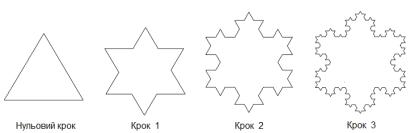
Рис.1. Перші 4 кроки побудови сніжинки Коха
Більш складна форма масштабної інваріантності називається самоафінністю. Афінне перетворення – це узагальнене перетворення подібності. Перетворення називається афінним, якщо воно неперервне і взаємно однозначне, а образом будь-якої прямої є пряма. Наприклад, в ході афінних перетворень правильні багатокутники перетворюються на неправильні, але трикутники залишаються трикутниками, чотирикутники – чотирикутниками і т.д. Відповідно, самоафінними об'єктами можна назвати такі, які складаються з частин, утворених в ході афінних перетворень цілого об'єкта. При цьому, згідно Мандельброту, самоафінність виключає обертання. Очевидно, що існують і більш загальні форми масштабної інваріантності. Головне для визначення фракталу є те, що його частини, які розглядаються в одному масштабі, в якомусь сенсі схожі на частини, що розглядаються в іншому масштабі.
Самоподібні об'єкти є штучними математичними об'єктами. Їх ще також називають регулярними фракталами. У природі строга подібність не зустрічається. Велика частина фрактальних об'єктів, які реально зустрічаються в природі, має властивість масштабної інваріантності, не будучи самоподібною в строгому сенсі цього слова. І ще одна відмінність: регулярним фракталам властива нескінченна подільність, але реальні фрактали є обмежені розмірами і позбавлені нескінченно малих деталей.
Розмірність фракталів. Другою важливою особливістю фракталів є їхня розмірність. Розрізняють два види розмірності метричну і топологічну.
Метрична розмірність, яка виражається цілим числом, що встановлює зв’язок між вимірюваним розміром фігури і одиницею вимірювання,
Топологічна розмірність геометричної фігури це число координат, необхідних для визначення положення точки, що лежить на цій фігурі.
Метрична та топологічна розмірності геометричної фігури є завжди виражені цілим числом, проте фрактали мають дробову розмірність. Так, положення точки на лінії визначається однією координатою, а на плоскій фігурі – двома координатами. Можна уявити n -мірну фігуру, але її топологічна розмірність завжди буде виражена цілим числом.
Класичним прикладом визначення фрактальної розмірності ломаного контуру є визначення контуру берегової лінії чи контуру державної границі. Тут суть метода полягає в тому, що довжину зрізаної лінії вимірюють відрізками кожен раз іншої довжини. При зменшенні розмірів відрізків довжина ломаної лінії цього контуру буде зростати. Виміряна довжина подається наближеною формулою
L a 1 D ,
де – розмір вимірювального відрізка; a – деякий постійний коефіцієнт; D – фрактальна розмірність.
Найчастіше для визначення фрактальної розмірності використовують метод покриття фрактального об’єкта регулярною сіткою з розміром чарунок . Використання цього методу полягає у покритті фрактального об’єкта такою сіткою і підрахунку кількості чарунок, в яких знаходяться будь-які елементи цього об’єкта.
В даний час існують різні підходи до виміру метричної розмірності об'єктів, але всі вони ведуть своє походження від розмірності Хаусдорфа, введеної ним для компактної множини, розмір якої N r вимірюється кількістю куль радіуса r , якими покривають цю множину. Розмірність Хаусдорфа визначається за формулою.
123
D r lim |
ln N r |
|
|
|||
|
. |
|
(1*) |
|||
ln 1/ r |
|
|||||
|
r 0 |
|
|
|
|
|
Якщо помножити обидві частини (1*) |
на ln 1/ r |
і ввести D під знак логарифму, |
отримаємо |
|||
співвідношення |
|
|
|
|
|
|
D |
~ N r або |
|
D |
~ N r , |
(2*) |
|
1/ r |
r |
|||||
де N r є мінімальна кількість куль радіуса r
Узагальнення розмірності Хаусдорфа на випадок необмеженої множини називають розмірністю Хаусдорфа-Безиковича. На практиці вимір цієї розмірності часто зводиться до виміру клітинної розмірності, коли вимірюваний об'єкт покривають не кулями одиничного радіуса, а клітинами (відрізками) з одиничною стороною. Саме про цю розмірності йшлося у прикладі з береговою лінією.
Визначимо клітинну розмірність сніжинки Коха. Будемо вимірювати розмір периметра N по мірі її побудови. Одиницями вимірювання u служитимуть сторони багатокутників, отримані в результаті кожного кроку її будови. Номери кроків позначимо n. Для вихідного трикутника n 0
маємо u0 1 , N0 3 . Далі в результаті кожного чергового кроку одиниця виміру буде зменшуватися в 3 рази, а периметр, виміряний у відповідних одиницях, буде збільшуватися в 4
рази: u |
|
1 |
, |
N 12 ; |
u |
|
|
1 |
, |
N |
|
48 |
; |
u |
|
|
1 |
|
, N |
|
192 |
і т.д. Це можна узагальнити для |
||||
1 |
3 |
|
1 |
|
2 |
9 |
|
|
2 |
|
|
|
|
|
|
3 |
27 |
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
n |
|
|
|
сніжинки Коха наступним чином: u |
|
|
|
; |
N 3 |
4 |
. Підставляємо отримані значення u і N у |
|||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 D |
|
|
|
|
|
D |
|
ln 4 |
1.26 . |
|
|
|
|
|||||||||
формулу |
N ~ |
|
. Отримуємо |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
ln3 |
|
|
|
|
|
|
|
|
|
|
||||
14.2. Фрактальний аналіз часових рядів
У ранніх роботах Мандельброт визначав фрактали як об'єкти, розмірність Хаусдорфа-Безиковича яких є більшою за їх топологічну розмірність. Однак згодом стало очевидно, що РХБ є лише однією з цілого сімейства дрібних розмірностей. Вище ми отримали деяку дробову розмірність часового ряду, що є аналогом РХБ при допущенні, що ряд має дещо, що назване розміром. Однак цей розмір досить важко інтерпретувати змістовно, і, крім того, пропонований вище спосіб визначення розмірності є досить трудомісткий.
Часовий ряд f yiti переважно відображається графічно на площині, оскільки кожен його
рівень може бути фіксований положенням точки з відомими координатами, тобто такий ряд можна розглядати як множину точок занурених в двовимірний евклідовий простір. Найбільш простим способом дослідження фрактальної структури часових рядів є обчислення їх характеристики через
клітинну розмірність Dc .
Подамо на відрізку a, b часовий ряд, що має скінченне число точок розриву першого роду. Розглянемо рівномірне розбиття даного відрізку.
|
|
|
|
|
|
m a t0 t1 tm b , |
(1) |
де t |
|
t |
|
|
b a |
, i 1, 2, , m . |
|
i |
i 1 |
|
|
||||
|
|
|
m |
|
|||
|
|
|
|
|
|
||
|
|
Покриємо графік даного ряду прямокутниками так, щоб це покриття було мінімальне за площею в класі |
|||||
покриттів прямокутниками з основою , як це зображено на рис. 14.1. Висота прямокутника на відрізку ti 1; ti |
|||||||
рівна амплітуді Ai , яка є різницею між максимальним і мінімальним значенням функції |
f t на цьому відрізку. |
||||||
Введемо величину
124

m |
|
V f Ai , |
(2) |
i 1
де Ai – амплітуда, яку розраховують як різницю між максимальним та мінімальним значеннями часового ряду.
Зміст цієї функції полягає в тому, що вона фактично є варіацією функції і відповідає масштабу розбиття на відрізку a, b .
Рис. 14.1. Побудова мінімального покриття. |
|
||
Тоді повну площу мінімального покриття S можна записати у вигляді |
|
||
S V f |
. |
(3) |
|
При цьому, виходячи з рівняння (1*) за аналогією замість r в нашому випадку маємо сторону |
|||
прямокутника , можемо вважати, що варіація функції f t є пропорційна стороні прямокутника |
, тобто: |
||
V f ~ |
|
при 0 , |
(4) |
|
|||
де |
|
|
|
D 1, |
|
(5) |
|
величина D називають розмірністю мінімального покриття.
Для одномірної функції топологічна розмірність DT 1, тому можна записати, що D DT . Отже,фактично вказує на відмінність між топологічною та фрактальною розмірностями, тобто його природно можна назвати індексом фрактальності і розглядати його як один з основних фрактальних показників.
V f приводить її до
швидкого виходу на степеневий асимптотичний режим (4). В результаті для обчислення індексу потрібно на два
порядки даних менше ніж для обчислення звичайних фрактальних показників. Використання цього показника розширює сферу застосування фрактального аналізу при вивченні різних природних, соціальних і технічних процесів. Індекс фрактальності може використаний як індикатор локальної стабільності часового ряду: чим більшим є його значення, тим стабільнішим є ряд.
Щоб зіставити розмірність D з іншими видами розмірностей і зокрема з клітинковою розмірністю |
Dc |
||||
побудуємо розбиття площини графіка клітинками як показано на рис. 2. |
ti 1, ti . Тоді з рисунку видно, |
||||
Нехай Ni – число клітинок, що покривають графік в середині відрізка |
|||||
що |
|
|
|
|
|
0 N |
i |
2 |
A 2 2 . |
|
(6) |
|
|
i |
|
|
|
Розділимо дане співвідношення на і просумуємо по i |
з врахуванням (2). В результаті отримаємо |
|
|||
125

|
|
0 N Vf 2 b a , |
(7) |
||||
де N Ni є повне число клітинок розміром , які покривають графік функції |
f t на відрізку a, b . |
||||||
Переходячи до границі при 0 і, враховуючи (4) і (5), отримаємо: |
|
||||||
|
|
N |
~ V |
f |
~ 1 D . |
(8) |
|
|
|
|
|
|
|
|
|
З другої сторони, оскільки з (3) V |
f |
S |
|
1 можемо записати |
|
||
|
|
|
|
|
|
||
|
|
N |
S |
c |
1 ~ 1 Dc . |
(9) |
|
|
|
|
|
|
|
|
|
Отже, Dc D . Зауважимо, що для реальних фрактальних функцій мінімальні і клітинкові покриття можуть давати
різні наближення величин S до асимптотичного режиму S ~ 2 D при 0 , де S – повна площа комплексу з масштабом розбиття , причому величина цієї відмінності може бути вельми значною.
14.3. Метод нормованого розмаху
Існує простий і осмислений спосіб фрактального аналізу динамічних рядів – метод нормованого розмаху. Цей метод дослідження не повною мірою висвітлений у статистичній практиці, проте він заслуговує на увагу. Пояснюється це тим, що метод Херста дозволяє виявляти в статистичних даних такі властивості, як кластерність, тенденцію слідувати за напрямом тренду (persistence), швидку зміну фаз регулярної та хаотичної динаміки (antipersistence) послідовних значень, фронтальність, наявність періодичних та неперіодичних циклів, здатність розрізняти «стохастичну» і «хаотичну» природу шуму. Він заснований на інтерпретації Мандельбротом робіт англійського гідролога Гарольда Херста, що досліджував закономірності зміни рівня води в річці Ніл. Відповідно до цього методу аналізується не сума самих даних, що становлять динамічний ряд, а розмах суми відхилень цих даних від середнього арифметичного, нормований шляхом ділення на стандартне відхилення. Суми відхилень підраховуються для різних періодів часу або для різної кількості послідовних моментів спостережень, які виступають в якості масштабу вимірювання.
Ґрунтуючись на великому фактичному матеріалі спостережень за стоками Нілу, Г.Херст виявив, що для великих значень n статистика Rn / Sn веде себе у відповідності з степеневою залежністю:
Rn ~ cnH ,
Sn
де n – кількість спостережень, Rn – розмах ряду, Sn – стандартне відхилення ряду, c – деяка константа і H – коефіцієнт Херста.
Нехай X t – це функція, що задає послідовні значення аналізованого часового ряду, де 1 t m. Тоді накопичені відхилення від середнього для деякого інтервалу будуть визначатися як
t |
|
|
|
|
|
|
||
X t X t |
|
m , де |
X m – середнє арифметичне по ряду в цілому. Нормований розмах |
|||||
X |
||||||||
i 1 |
|
|
|
|
|
|
||
на інтервалі визначається наступним чином: |
|
|||||||
|
|
|
|
R t |
max X t min X t |
|
||
|
|
|
|
|
|
|
|
, |
|
|
|
|
S t |
S t |
|||
де R t – різниця максимального і мінімального накопиченого відхилення на даному інтервалі, а S t – стандартне відхилення.
126

Відповідно до формули Херста, |
R t |
a t H , де a |
і H |
– деякі константи. Константа H |
S t |
може змінюватися від 0 до 1 і називається показником Херста. Вона характеризує кут нахилу графіка лінійної залежності ln R / S від ln t . Свого часу Херст на основі великого емпіричного
матеріалу продемонстрував, що всупереч передумовам багатьох теоретиків цей показник для багатьох природних процесів може бути більший за 0,5 і звичайно дорівнює приблизно 0,7. Тому при H 0,7 формулу Херста називають емпіричним законом Херста.
Показник Херста може бути основою для визначення дробової розмірності динамічного ряду, що обчислюється як D 2 H . Він має, стосовно застосування до часових рядів, певний
зміст. Значення H і D характеризують міру «зламуваності» процесу. При H 0,5 |
( D 1,5 ) |
значення ряду різко змінюються, тобто процес володіє довготривалою знакозмінною тенденцією і називається антиперсистентним. Коли H наближається до 0, графік ряду ніби прагне заповнити
собою деяку площину, перетворитися з лінії в плоску фігуру, |
що відповідало б |
D 2 . При |
H 0,5 ( D 0,5 ) ряд має властивості так званого «білого шуму», тобто значення ряду абсолютно |
||
незалежні і між ними немає автокореляцій. При 0,5 H 1 |
(1 D 1,5 ) у ряді |
має місце |
автокореляція і накопичення змін призводить до появи довготривалої тенденції з зростанням або спаданням. Процес в цьому випадку називають персистентним. Ця тенденція може бути проявом довгого неперіодичного циклу. Значення ряду при цьому як би шикуються уздовж лінії, що виражає таку тенденцію, і в решті решт, коли H 1, збігаються з цією лінією, розмірність якої буде D = 1.
14.4. Обчислення показника Херста |
|
Нехай маємо послідовність спостережень |
x1, x2, , xn , , де індекси є значеннями |
часового параметра, тобто xi x ti . В загальному члени часової послідовності є випадковими
величинами. Для обчислення показника Херста з початкового часового ряду формуються окремі послідовності
y1 x1 x ,
y2 x1 x2 2x ,
y3 x1 x2 x3 3x , |
(*) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
yN x1 x2 xN N x 0 |
|
|
|
|
|
|||||
де x x1 x2 xN / N . |
|
|
|
|
|
|||||
Обчислюється величина розмаху |
R max yi min yi . При цьому припускається, |
що має |
||||||||
|
|
|
|
|
|
|
|
i N |
i N |
|
місце асимптотика |
|
|
|
|
|
|
|
|
||
|
|
|
|
R |
~ const N h |
при N , |
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
S |
|
|
|
|
|
|
в якій S 2 |
1 |
x x 2 |
x x 2 |
x |
|
x 2 |
. |
|
||
|
N |
|
||||||||
|
N |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина h і є показником Херста. |
|
|
|
|
||||||
Для знаходження наближеного значення h за експериментальними |
даними |
|||||||||
використовується лінійна апроксимація (регресія) |
ln R / S для декількох значень N . |
|
||||||||
Теоретичне вивчення показника Херста є досить складним, а тому на практиці приймають таке твердження.
127
Нехай |
D |
|
1 |
y |
|
y 2 y |
|
y 2 |
y |
|
y 2 |
– статистична дисперсія |
в |
||||||||
|
|
|
2 |
N |
|||||||||||||||||
|
|
|
N |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
послідовності |
(*), а |
y |
1 |
y |
y |
|
y |
|
. Якщо |
D |
|
має |
асимптотику const N 2h , то |
h |
|||||||
|
2 |
N |
|
||||||||||||||||||
|
|
|
|
|
N |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
збігається з показником Херста. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14.5. R/S аналіз часових рядів |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Основою цього методу є безрозмірне відношення |
|
R |
, яке в результаті свого визначення і |
||||||||||||||||||
|
S |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
інтерпретації дає всі підстави для проведення достатньо репрезентативного аналізу часового ряду та визначення показника Херста. Переважно в рамках такого дослідження увага акцентована саме на обчислення цього показника. Зміст методики R/S-аналізу можна подати послідовністю таких кроків.
Отже, нехай розглядається часовий ряд Z , що складається з елементів zi :
Z zi , i 1, 2, , m , (1)
де m – кількість спостережень, що формують ряд.
Крок 1. Процедура R/S-аналізу є переходом вихідного ряду Z до ряду Y , який складається з m 1 елементів yi , кожен з яких отриманий за формулою:
yi |
lg zi |
|
|
, i 1, 2, , m 1. |
(2) |
|
lg zi 1 |
|
|||||
|
|
|
||||
Оскільки доцільність переходу від вихідних елементів ряду до відношення логарифмів наступного та попереднього рівнів ряду не є незаперечною і залежить від специфіки досліджуваного ряду, тому перший крок переважно опускають. При цьому мають на увазі, що вказана процедура є різновидом додаткової обробки вихідних даних, а тому в разі необхідності до вихідного ряду може бути застосована різного роду попередня обробка, а не лише та, яка наведена в (2).
Крок 2. На цьому кроці визначають величину 1 та формують послідовність довжин відрізків, на які розбивається вихідний ряд:
|
|
|
|
n1, n2, , nk , nl , |
(3) |
де nk 1 nk , для всіх |
k від 1 до l 1. Максимальне значення l |
визначається за формулою: |
|||
m |
. Ця вимога означає те, що максимальна довжина відрізка nl |
має дозволяти розподілити |
|||
nl |
|
|
|||
|
|||||
|
2 |
|
|
|
|
загальний ряд довжини m хоча б на два відрізки однакової довжини (з однаковою кількістю елементів). Практично, найбільш відповідним є підхід до формування послідовності довжин відрізків (3), за якого виконується емпіричним шляхом отримане правило, що nk 10 , тобто
мінімальна довжина відрізка має бути не менше 10. Крім того, пропонується обирати лише ті
значення nk |
з |
набору (3), які є дільниками числа |
m , |
тобто m має бути кратне nk . |
Тому |
||||||
переважно дотримуються саме цих обмежень на значення nk , тобто nk 10 , а m є кратне nk . |
|
||||||||||
Подальші кроки реалізуються для всіх значень k |
від 1 до l . |
|
|
||||||||
Крок 3. Для чергового значення індексу k ряд |
Z |
розбивається на відрізки довжини |
nk , |
||||||||
кількість яких |
r |
|
визначається |
за співвідношенням: |
r |
|
m |
. Позначимо такі відрізки |
Z t |
, їх |
|
|
|
||||||||||
|
|
k |
|
|
k |
|
nk |
k |
|
||
елементи zt |
, |
|
|
|
|
|
|
|
|
||
|
j 1, 2, , n ; |
t 1, 2, , r . Відрізки Z t мають таку властивість, що вони не |
|||||||||
j |
|
|
|
k |
k |
|
k |
|
|
||
128

перетинаються (тобто містять унікальні елементи вихідного ряду). Для кожного відрізка Zkt
визначається середнє значення zt за формулою
|
|
|
|
1 |
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
zt |
|
|
ztj , |
|
t 1, rk . |
(4) |
||||||||||||||||||||||||||||
|
|
n |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Крок 4. |
Для кожного відрізка Zkt |
обчислюється ряд накопичених відхилень, елементи |
|||||||||||||||||||||||||||||||||
якого xtj визначаються за формулою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xtj zit |
zt , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
j 1, nk . |
(5) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
На основі значень накопичених відхилень для кожного відрізка Zkt |
визначається величина |
||||||||||||||||||||||||||||||||||
розмаху за формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rt max xt |
|
min xt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
, |
|
t 1, r . |
(6) |
||||||||||||||||||||||||||||||
|
k |
1 j nk |
|
|
|
j |
1 j nk |
|
j |
|
|
|
|
|
|
|
|
|
k |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Крок 5. Для кожного відрізка Zkt обчислюється його середньоквадратичне відхилення за |
|||||||||||||||||||||||||||||||||||
формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Skt |
|
|
|
|
|
1 |
|
|
ztj |
zt 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
, |
|
t 1, rk . |
(7) |
||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Після цього для кожного відрізка визначається нормоване (на середньоквадратичне |
|||||||||||||||||||||||||||||||||||
відхилення) значення розмаху: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R t |
|
Rt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
, |
|
|
|
t 1, rk . |
(8) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Skt |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
S k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Крок 6. |
Для кожного k |
обчислюється |
середньоарифметичне |
значення нормованих |
|||||||||||||||||||||||||||||||
розмахів, визначених за формулою (8): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
R |
|
|
|
|
|
|
1 |
|
rk |
R |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
k 1, l . |
(9) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
S |
k |
|
|
r |
S |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
k |
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Крок 7. |
Для кожного k обчислюється логарифм довжини відрізка nk , що відповідатиме |
||||||||||||||||||||||||||||||||||
абсцисі точки при подальшій побудові графіка ( xk ), |
а також логарифм усередненого значення |
||||||||||||||||||||||||||||||||||
R
нормованих розмахів , обчисленого за формулою (9). Останній відповідатиме ординаті
S k
зазначеної точки ( yk ). У символьному вигляді це такі формули:
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|||
xk lg nk , |
yk lg |
|
|
, |
k 1, l . |
(10) |
||
|
||||||||
|
|
S k |
|
|
|
|
||
Крок 8. Використовуючи отримані за формулою (10) |
значення xk та yk , методом |
найменших квадратів будується рівняння лінійної регресії: |
|
y a x b . |
(11) |
Коефіцієнт a в побудованому на основі фактичних даних xk |
та yk рівнянні (11) відповідає |
усередненій оцінці показника Херста H для часового ряду Z . |
|
129
Існує багато різних методик проведення R/S-аналізу, проте, попри свою обчислювальну трудомісткість і вибагливість до обсягів інформаційних масивів, є найкращою з точки зору отримання абсолютного значення показника Херста для ряду даних у цілому. 1
130
