
ms_lec
.pdfМОДЕЛЮВАННЯ СИСТЕМ
ЛЕКЦІЯ 15
ФАЗОВИЙ АНАЛІЗ ЧАСОВИХ РЯДІВ
Пояснено основні поняття фазового аналізу – фазові простір і площина, фазові портрети, фазові траєкторії, атрактори. Розглянуто основу методів нелінійної динаміки. Приведені метод побудови фазових портретів та побудова квазіциклів часових рядів. Подано основні харакеристики квазіциклів та вказано їх значення для визначення фазового стану системи.
15.1. Основні поняття фазового аналізу
Особливістю математичного моделювання складних систем є те, що забезпечуючи вимоги, які ставляться до моделі, і в першу чергу досягнення максимальної відповідності моделі оригіналу, модель може виявитися не менш складною ніж оригінал, трудно інтерпретованою, а робота з нею доки не будуть отримані результати виявиться в часі дуже запізнілою. Тому, для складних систем переважно будують частинні моделі, які характеризують модельовану систему окремо різними показниками. За такого підходу система подається окремими моделями, які в той чи інший спосіб відображають її функціонування і дають підстави для її вивчення.
Одним із напрямків у сучасному дослідженні та аналізі складних систем є використання, безпосереднє або адаптоване, методів нелінійної динаміки. Ці методи застосовуються для розв’язку задач обробки складних та випадкових сигналів із широким спектром, у тому числі, хаотичних, найчастіше нестаціонарних, з метою оцінки параметрів або знаходження наближеної форми рівнянь, що їх описують, як в просторі, так і в часі.
Поширення комп’ютерної обробки інформації визначило представлення часових залежностей у вигляді дискретної послідовності відліків – часових рядів. Такий вид мають сигнали на виході аналого-цифрових перетворювачів, цифрових вимірювальних приладів і т.п. Обробка таких часових залежностей може виконуватися безпосередньо – візуально, як оцінюють кардіота енцефалограми лікарі-діагности; на основі розрахунків класичних статистичних характеристик (Фур'є- та вейвлетспектри, функції кореляції й ін.), а також – розвинутих у рамках теорії коливань і нелінійної динаміки (якісний аналіз фазових портретів, траєкторій і оцінки різних кількісних характеристик атракторів у фазовому просторі,). Це дозволяє вирішувати задачі кластеризації сигналів, оцінювати взаємозв'язок між їхніми джерелами та ін.
Окремою задачею у контексті даного напрямку є задача реконструкції математичних моделей за часовими рядами, які генеруються системами, модельні рівняння яких апріорно (частково або повністю) невідомі. Наявність математичної моделі дозволяє вирішувати задачі прогнозу подальшого поводження системи у часі або при зміні її параметрів, оцінки адекватності уявлень про об'єкт, спостереження величин, недоступних прямому вимірові. Маючи у своїй передісторії класичну задачу апроксимації точок на площині гладкою кривою, завдяки розвитку обчислювальної техніки, досягненням нелінійної динаміки, зокрема, формуванню концепції динамічного хаосу, у даний час мова йде про реконструкції моделей у вигляді диференціальних і різницевих рівнянь.
В останні роки показано, що хаос не тільки не заважає, а, скоріше, є обов’язковою умовою працездатності складних систем. Тільки завдяки наявності хаотичного атрактора, який містить, як
131
правило, нескінченну кількість нестійких періодичних циклів, можна досягти якісної зміни динаміки системи (переходячи із околу одного циклу до іншого) за рахунок малих збурень системних параметрів. У зв’язку з цим окремою є задача стабілізації апріорі заданих траєкторій хаотичних динамічних систем, розв’язання якої дуже часто пов’язане із проблемою відновлення диференціальних рівнянь на основі заданої множини точок у фазовому просторі, які належать атрактору системи. Отже проблеми керування хаосом і реконструкції модельних рівнянь є взаємозв’язаними, належать до одного класу задач теорії нелінійних систем. Згадані терміни можна подати такими визначеннями.
Визначення 15.1. Дисипативні системи – динамічні системи, які описуються кінетичними рівняннями, в яких змінними можуть бути будь-які фізичні величини, наприклад, концентрації частинок певного роду, температура тощо.
Визначення 15.2. Фáзовий простір – багатовимірний простір, утворений змінними даної динамічної системи.
Визначення 15.3. Фазовою траєкторією називають тренд (тенденцію) еволюції системи, описану кривою в цьому фазовому просторі.
Визначення 15.3. Фазовий портрет – це сукупність різних можливих фазових траєкторій. Фазовий портрет дивного аттрактора - це не точка і не граничний цикл, а деяка область, в якій відбуваються випадкові блукання.
Визначення 15.4. Атрактор (від англ. attract – притягати) – множина точок у фазовому просторі, до якої збігаються фазові траєкторії дисипативної системи.
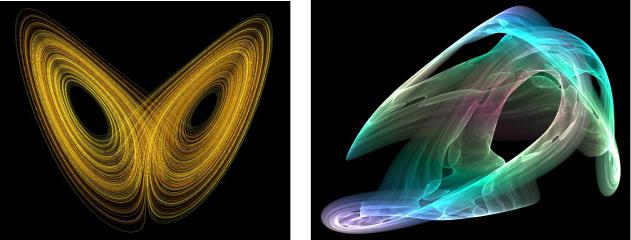
Рис. 15. 1. Форми атракторів: атрактор Лоренца (зліва) та «дивний атрактор» (справа).
Атрактори можуть бути точковими (точки рівноваги), лініями (граничні цикли), різної форми поверхнями, і навіть складними багатовимірними фрактальними структурами, як у випадку дивного аттрактора, зображеного на рис. 15. 1 (справа).
Визначення 15.5. Атрактор – сукупність внутрішніх і зовнішніх умов, що сприяють «вибору» самоорганізовуваною системою одного з варіантів її сталого розвитку, ідеального кінцевого стану, до якого прагне система у своєму розвитку.
Визначення 15.6. Зона атрактора – це простір всередині атрактора, в якому кожна частинка (система), яка туди потрапила, поступово зміщується в заданому напрямку.
В методології синергетики розрізняють прості і дивні атрактори. При станах системи, що визначаються простим аттрактором, траєкторія розвитку системи є передбачуваною. При станах системи, що визначаються дивним аттракторів, стає неможливим визначити положення частинок (їх поведінку) в кожен даний момент, хоча ми і впевнені, що вони знаходяться в зоні аттрактора.
Метод фазових портретів виник одночасно з інтегральним і диференціальним обчисленням і також пов'язаний з ім'ям Ньютона. Спочатку цей метод застосовувався до одномірним системам, пізніше Ж.А. Пуанкаре, а потім А.М. Ляпунов, перенесли його на аналіз двовимірних систем. Сучасні складні системи є багатовимірними системами, заданими великим числом диференціальних рівнянь.
132
Основна ідея фазових портретів одновимірних, двовимірних і багатовимірних систем – це виявлення характерних точок і ліній. Попри значні різноманітності руху системи на фазовій площині характерні точки і лінії повільно еволюціонують і можуть розглядатися в першому наближенні як нерухомі. Ця властивість на початку 1970-х лягла в основу принципу стабільності динамічних систем. Фазові портрети багатовимірних систем володіють структурою, в якій області з від’ємним зворотним зв'язком чергуються з областями з додатним зворотним зв'язком.
15.2. Інструментарій фазових портретів
Візуальна оцінка даних в нелінійних динамічних системах важлива тому, що вони, як правило, не мають єдиного рішення. Зазвичай, існує деяка невелика множина, а можливо і нескінченна кількість, цих рішень. У минулому, ця обставина змушувала дослідників уникати розгляду нелінійних систем.
Нинішні широкі графічні можливості персональних комп'ютерів дозволяють нам побачити цю величезну множину можливих рішень. Багато хаотичних систем мають нескінченну кількість рішень, локалізованих в обмеженій частині простору, і ця множина можливих рішень часто має фрактальну розмірність.
Оглядати дані неважко, якщо нам відомі всі змінні системи. Ми просто наносимо їх на координатну площину. Якщо змінних дві, то одну з них приймаємо за x , іншу за y і викреслюємо
залежність в декартових координатах, тобто наносимо величину однієї з них щодо значення іншої в один і той же момент часу. Такий графік фактично і є фазовим портретом системи, а область обмежена осями координат подається як фазовий простір. Розмірність фазового простору залежить від кількості змінних в системі. Якщо вона включає в себе дві або три змінних, можна спостерігати дані візуально. Якщо розмірність системи більше трьох, то це вже робиться математичними методами.
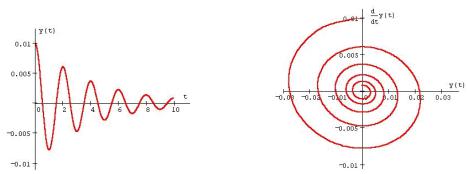
Важливі три основні класи нелінійних систем. Кожен з них має свій власний тип «атрактора» (область точки притягання траєкторії) у фазовому просторі. Найпростішим типом є точковий атрактор. Приклад системи з точковим атрактором - маятник, з тертям. Коли маятнику надається початкова енергія, він починає розгойдуватися, але зважаючи на тертя амплітуда його коливань поступово зменшується, поки маятник зовсім не зупиниться. Змінними в такій системі виступають швидкість і положення тягарця. Якщо будь-яку з цих змінних виокремити як часовий ряд, то результуюча хвиляста лінія поступово зменшуватиме свою амплітуду до нуля – крива переходить в пряму лінію – маятник зупинився. Якщо фазовий портрет цієї системи подати в координатах положення – швидкість, то отримаємо спіральну криву, яка закінчується в початку координат, коли маятник зупинився.
а) |
б) |
Рис. 15. 2. Затухаючі коливання і їх фазовий портрет.
Якщо надати маятнику велику початкову енергію, часовий ряд і фазовий портрет системи будуть володіти більшою початковою амплітудою, але за якийсь час часовий ряд знову матиме нульові значення, а його фазовий портрет – перейде в початок координат. Можна сказати, що в
133

цьому фазовому просторі система «притягається» до початку координат, тобто, де б вона не брала свій початок, вона приходить в початок координат – до свого рівноважного стану.
Якщо припустити, що маятник не має тертя і надати йому поштовх такої сили, щоб вихідна точка гойдання була як най далі від положення рівноваги, відповідно до ньютонівської фізики, в даному випадку, будемо мати атрактор маятника, який не гальмується тертям або гравітацією.
В цьому випадку, часовий ряд швидкості або положення буде синусоїдою, а фазовий портрет – замкнутим колом. Радіус цього кола залежатиме від сили «поштовху», наданого маятнику, але коло залишається колом, рис. 15.3. Цей тип атрактора називають граничним циклом, оскільки він характеризує регулярну періодичну систему, в тому числі і маятник з наданням енергії ззовні.
Рис. 15. 3. Фазовий портрет |
Рис. 15. 4. Неповторюваність фазових траєкторій. |
|
типу граничний цикл. |
||
|
Класичний підхід розглядає більшість систем як системи рівноважні (з точковими атракторами) або як такі, що періодично коливаються близько точки рівноваги (з атракторами типу граничний цикл).
Однак емпірично таке бачення ситуації не підтверджується. В значній своїй більшості часові ряди характеризуються неперіодичними циклами (тобто не мають «характеристики довжини» або «часового масштабу»). Такі неперіодичні цикли характерні для нелінійних динамічних систем.
Послідовність неперіодичних циклів властива останньому типу атрактора – хаотичному або «дивному» атрактору. Припустимо, що ми випадковим чином змінюємо величину наданої енергію, але час між поштовхами залишається однаковим. Вплив енергії буде тепер змінним і пов'язаним з силою попереднього поштовху, незважаючи на те, що величини поштовхів відносно незалежні. Оскільки ми надаємо поштовхи енергії, випадкові за своєю силою, але через рівні проміжки часу, положення і швидкість маятника будуть щоразу іншими. Наприклад, під час другого поштовху маятник може направлятися вже вниз. Якщо цей другий поштовх буде малий, то маятник може рухатися вгору, коли він отримає третій поштовх, який приведе до уповільнення маятника. Отже, незважаючи на те, що маятник отримує поштовхи енергії з регулярними інтервалами, його фазовий портрет буде відрізнятися в кожному циклі. Цикл від вершини до вершини гойдання характеризує собою орбіту.
Оскільки маятник щоразу не може завершити цикл, його фазовий портрет буде складатися з орбіт, які ніколи не будуть однаковими і не будуть періодичними, як показано на рис 15. 4. Такий фазовий портрет виглядає випадковим і хаотичним, але він обмежений певними межами (максимальною амплітудою маятника) і завжди буде обертатися за годинниковою стрілкою, хоча розміри орбіт і час їх проходження будуть різними.
Таким чином, маємо хаотичний або «дивний» аттрактор. Дивний аттрактор містить в собі всі можливі траєкторії. Рівновага представляється не точкою, а областю у фазовому просторі, точніше обмеженою областю з нескінченною кількістю рішень. Такий фазовий простір дає нам картину можливостей системи.
134
Для систем, рівняння яких відомі, сконструювати фазовий простір нескладно. Якщо ж природа системи невідома, але спостерігається якийсь ефект, то фазовий простір може бути відновлено за даними.
15.3. Основа методів нелінійної динаміки
Методи нелінійної динаміки базуються на методах аналізу часових рядів та реконструкції атрактора. Нагадаємо, що часовий ряд це множина хронологічно (за часом) впорядкованих
значень z j , , zL |
j 1, 2, , L . |
|
|
|
|
Якщо дано числовий ряд конкретних значень величин |
|
||||
|
|
|
|
|
|
|
z j , |
j 1, n , |
(2.10) |
||
то його зазвичай називають «траєкторією», яку розглядають як ряд спостережень – часовий ряд. Постає питання про характер поведінки системи, виходячи з ряду (2.10). Чи є поведінка цієї
системи детермінованою, тобто чи існує рівняння, яке забезпечує повне визначення поведінки системи? При цьому, питання знаходження такого рівняння не є самоціллю, бо нас цікавить передбачення поведінки системи на певне число кроків вперед (прогнозування). Глибина, тобто число кроків прогнозу визначається в цьому випадку ляпуновскими показниками.
Виникає природне запитання: як за відомою (початково) множиною
передбачити значення zl 1, zl 2 , , і т.д. Сукупність цих та інших питань називають проблемою
прогнозу або завданням побудови предиктора (від англ. to predict – передбачити).
Незаперечною заслугою теорії хаосу є введення терміну атрактор і широка пропаганда знань про біфуркації атракторів. Вони мають фрактальну структуру, і є невід'ємною складовою хаотичних коливань.
Зазначена вище динаміка процесу (тобто послідовність рішень задачі) часто представляється у вигляді коливань навколо деякого «середнього» або в межах деякого «інтервалу». Встановити асимптотику поведінки цих «флуктуацій» – завдання дуже непросте. Серед принципових питань вирішення цього завдання першим стоїть питання про присутність хаосу або, навпаки, регулярності (періодичності) в динаміці процесу.
З математичної точки зору хаос характеризується двома основними особливостями:
а) при деяких значеннях параметрів майже всі початкові умови призводять до аперіодичної динаміки;
б) за як-завгодно близьких початкових умов рух системи буде різним.
Термін «аперіодична динаміка» означає, що зміна величини, яку спостерігають не має регулярного, періодичного характеру. При цьому термін «хаос» і «шум» мають різний зміст. До теперішнього часу не має якого-небудь загального методу, який би дав відповідь на питання: чи обумовлений спостережуваний динамічний процес шумом, чи являє собою хаотичну поведінку. Для ідентифікації хаотичної поведінки часто знаходять застосування дві статистичні міри хаосу – число Ляпунова та фрактальна розмірність. Число Ляпунова відображає собою регулярність, а фрактальна розмірність – геометрію динаміки (руху). В іншій інтерпретації фрактальна розмірність системи, тобто розмірність області значень її показників або критеріїв показує ступінь покриття або заповнення виділеного для цієї області простору. Якщо фрактальна розмірність системи менше її топологічної розмірності, то у виділеному просторі будуть існувати «порожні» підобласті, тобто коефіцієнт заповненості виділеного простору буде меншим за одиницю.
Математична модель будь-якої динамічної системи S представляє собою деякий фазовий простір F Z zl r , zl r 1, , zl r m , r 0, 1, 2, з визначеним у ньому оператором зміни
фазового стану системи. Переважно, в якості такого оператора приймають впорядкований процес |
|
подання в декартових координатах послідовності точок zl , zl 1 , |
l 1, 2, , n 1, де n – |
довжина розглянутого часового ряду. Для наочності на графіку ці точки можуть бути з'єднані дугами, або відрізками кривих.
Математичні моделі динамічних систем класифікуються залежно від структури їх фазового простору F Z і виду оператора.
135
При цьому в першу чергу розрізняють випадки дискретної і неперервної зміни в часі фазового простору. Оператори прийнято класифікувати за їх властивостями (лінійний, нелінійний, неперервний і т.д.) і за формою завдання (диференціальна, інтегральна, матрична, таблична і т.д.). У випадку дискретних часових рядів об'єктом дослідження є дискретний (фазовий) простір, а тому обраний оператор не має властивості неперервності та лінійності і є заданий, переважно, у табличній формі. При цьому математичним образом динаміки системи є її фазовий портрет, який дає не тільки геометричне зображення окремих рухів, станів рівноваги, періодичних, хаотичних рухів, а й визначає «логіку» поведінки системи, його залежність від параметрів.
Накопичена до теперішнього часу надзвичайна розмаїтість рухів детермінованих динамічних систем може бути розділена на два основних типи, які можна трактувати як порядок і хаос, регулярність і нерегулярність.
У разі дискретних систем розбиття рухів на регулярні та хаотичні характеризує тільки їх часову поведінку. У разі розподілених систем мова може йти не тільки про часовий, а й про просторовий порядок і хаос, про періодичність та аперіодичність, регулярність і нерегулярність не тільки часової, але і просторової структур.
Адекватним математичним чином часового порядку і хаосу стали атрактори, тобто стійкі стани рівноваги, стійкі періодичні рухи або автоколивання і, нарешті, дивні атрактори. Використовуючи метод візуалізації дивних атракторів можна отримати суттєву якісну інформацію про модельовані об'єкті.
Математичні моделі з просторовим або часовим хаосом не враховують внутрішню структуру досліджуваної системи. Однак ця структура може істотно впливати на поведінку динамічної системи.
Проблема управління нелінійною системою (хаос можливий тільки в нелінійних динамічних системах) розглядається нижче лише у випадку дискретного фазового простору.
Мета використання методу псевдофазового простору полягає в тому, щоб побудувати |
||||
залежність величини від значень цієї ж величини, але в інші моменти «часу» |
z j k y t j k . |
|||
Іншими словами, |
питання |
полягає в |
знаходженні або визначенні |
такої функції |
z j , z j 1, , z j m 1 , яка дозволяла б прогнозувати значення z j m . |
|
|||
При виконанні |
певних |
умов проблема |
побудови обґрунтування зазначеної функції |
|
задовільним чином вирішується за допомогою теореми Такенса. Проте, в цій лекції основну увагу приділено питанню про те, якою мірою можуть виявитися корисними для прогнозування якісні висновки, одержані за допомогою візуалізації розглянутого фазового простору, оскільки, працюючи з одномірними часовими рядами є підстава вважати інформативним фазовий простір, який має розмірність 2, тобто простір точок в декартових координатах
z j , z j 1 , j 1, 2, . (2.11)
В процесі використання методів візуалізації керуються тим, що фазова траєкторія (2.11) являє собою набір точок, які послідовно переходять одна в одну. Іншими словами, положення кожної точки в послідовності (2.11) однаково визначається положенням у попередній точці. Таким чином, існує деяка функція , яка зв'язує між собою положення двох точок, які слідують одна за
одною: |
|
z j 1 z j . |
(2.12) |
Співвідношення (2.12) визначає точкові відображення. Використання точкового відображення (2.12) при дослідженні динаміки конкретних систем виявляється досить корисним, як в силу його наочності, так і в обчислювальному відношенні, оскільки при переході до відображення розмірність системи, що вивчається зменшується на одиницю.
Зауважимо що кінцеві відображення виду (2.12) можуть бути визначені і поза будь-яким зв'язком з якими-небудь конкретними системами рівнянь.
15.4. Побудова фазового портрету
136

В арсеналі сучасних методів аналізу та моделювання хаотичних часових рядів щораз більшого значення набуває візуалізація їх фазових портретів, які одержують в інтерактивному режимі з використання комп’ютерів. Як відомо, при побудові фазового простору для конкретного часового ряду принципово важливим є питання про його розмірність . Ця розмірність повинна
бути не меншою, ніж розмірність аттрактора спостережуваного ряду. Таким чином, одномірні часові ряди візуалізуються в двовимірному фазовому просторі, тобто в просторі з розміріністю2 . Це можна пояснити так. Справа в тому, що в такому просторі часовий ряд подається двома
змінними: в якості незалежної змінної виступають значення рівнів часового ряду, а в якості залежної (функції) – швидкість зміни значення кожного рівня.
Для ілюстрації процедури побудови фазового портрета розглянемо часовий ряд, який подає функціонування людино-машинної системи, а точніше людино-машинного інтерфейсу обробки візуальної інформації. Діяльність людини-оператора в такому інтерфейсі є пов’язана з опрацюванням, пред’явленої оператору на моніторі, послідовності однорідних за тлом зображень, на яких необхідно виявити об’єкти зхаданого класу і проаналізувати існуючу ситуацію, щоб прийняти адекватні в кожному випадку рішення. Прикладами такої діяльності є обробка текстових документів, різноманітних рахунків, оперативне опрацювання аерокомічних зображень в режимі он-лайн, результати флюроскопії, рентгенівських знімків, пошуку дефектів матеріалу (наприклад прокату, зварних швів), зображень морського дна тощо. Майже аналогічною є діяльність, коли за регулярним чи випадковим сигналами потрібно слідкувати за декількома моніторами чи табло.
Особливістю таких видів діяльності є значна концентрація уваги, монотонія, гіподинамія, які впродовж робочої зміни стимулюють розвиток нервової напруженості, погіршення функціонального стану та зростаюче погіршення зорових, психомоторних та когнітивних характеристик оператора, а відтак і зриву в його роботі – прийняття невідповідних рішень.
Основними критеріями ефективності такої діяльності є оперативність вибору і прийняття рішення та кількість допущених помилок, іншими словами, оператор має за найменшої кількості помилок приймати з максимальною ймовірністю правильні рішення.
Всучасних системах підготовки висококваліфікованого операторського персоналу, зокрема
втренажерних системах широко використовуються різноманітні тестові завдання, які з однієї сторони моделюють конкретну операторську діяльність в реальному робочому середовищі, а з другої – на підставі результатів контролю забезпечують ефективне і об’єктивне оцінювання рівня кваліфікації реципієнта. Тестові завдання є розподіленими в часі і можуть демонструватися як дискретно (окремі зображення), так і неперервно (відео), проте результати вимірювань, як правило, є завжди дискретними. Такі дані подають виміряні значення досліджуваних показників разом фіксованими моментами отримання цих значень в реальному часі, тобто у вигляді часових рядів. Часові ряди відносяться до класу дискретних випадкових процесів і досить широко використовуються в різних предметних галузях. Основною характерною рисою часових рядів є те, що вони подають поведінку вимірюваного показника протягом усього часу його спостереження. Такі ряди для двох операторів зображені на рис. 15.5.
Значення рівнів [ms]
|
|
|
|
|
|
Часовий ряд оператора Оп-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Часовий ряд оператора Оп-10 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1600 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ms] |
1400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рівнів |
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значення |
800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
11 |
21 |
31 |
41 |
51 |
61 |
|
71 |
|
|
|
|
81 |
91 |
101 |
|
|
|
1 |
11 |
21 |
31 |
41 |
51 |
61 |
|
|
71 |
81 |
91 |
101 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номери рівнів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номери рівнів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 15. 5. Індивідуальні часові ряди операторського персоналу.
137

Оцінювання операторської діяльності, пов’язаної з опрацюванням інформації, наданої на моніторі у вигляді послідовності, статистично однорідних за тлом, зображень з об’єктами пошуку заданого класу, здійснюють на підставі отриманих результатів. Кожне таке зображення характеризується певним часом опрацювання, після чого оператор приймає відповідне рішення, момент якого фіксується. Повний час опрацювання зображення – з моменту його появи на моніторі і включно до моменту прийняття рішення є значенням показника оперативності. Значення показників і моменти прийняття рішень подають як індивідуальний часовий ряд даного оператора.
Кількісними характеристиками індивідуальної діяльності, в таких випадках, є показники описової статистики, які помимо вибіркових числових характеристик: середнього арифметичного, дисперсії, середньоквадратичного відхилення та розмаху включають включають параметри їхнього розподілу – медіану, моду, асиметрію та ексцес. В якості моделі даних різні моделі, але які включають рівняння тренду. Саме тренд, який описує траєкторію поведінки вимірюваного показника, вичерпує інформацію про динамічну складову індивідуальної операторської діяльності. За більш докладних досліджень застосовують методи спектрального аналізу, розглядають автокореляцію та інші методи, які входять в лінійну парадигму статистичної обробки даних.
Фазові портрети. За означенням фазовий аналіз це відображення диференціалу функції на її оригнал. Для проведення фазового аналізу і в першу чергу побудови фазового портрету необхідно, на підставі оригінального часового ряду визначити швидкість зміни його рівнів. Відомо, що шидкість зміни показника характеризується його диференціалом.
Оскільки отримані часові ряди є дискретними, а їхня обвідна не є гладкою монотонною функцією використовуємо формально метод чисельного диференціювання. В результаті застосування до оригінальних часових рядів формул чисельного диференціювання
|
y1 y 1 2h і/або |
y2 8y1 8y 1 y 2 12h , |
y |
будують фазові портрети, зображені на рис. 15.6.
За допомогою табличного процесора MS Excel 2003, використовуючи Майстер діаграм і вкладка Стандартна, на якій вибираємо опцію – Точкова діаграма зі значеннями (маркерами) з’єднаними згладжуючими лініями.
|
|
Фазовий портрет оператора Оп-3 |
|
|
|||
|
1200 |
|
|
|
|
|
|
значення |
1000 |
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференційовані |
600 |
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
|
-200 |
|
|
|
|
|
|
|
|
|
Оригінальні значення рівнів |
|
|
||
|
|
Фазовий портрет оператора Оп-10 |
|
||||||
|
1200,00 |
|
|
|
|
|
|
|
|
значення |
1000,00 |
|
|
|
|
|
|
|
|
800,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференційовані |
600,00 |
|
|
|
|
|
|
|
|
400,00 |
|
|
|
|
|
|
|
|
|
200,00 |
|
|
|
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
|
-200,00 |
|
|
|
|
|
|
|
|
|
|
|
Оригінальні значення рівнів |
|
|
||||
Рис. 15.6. Фазові портрети індивідуальних часових рядів.
Оскільки, в локалізації траєкторій фазового портрету спостерігається хаотичне нагромадження ніби замкнених траєкторій можна припустити існування циклічності, фактичну наявність якої можна встановити лише виділенням окремих циклів. Як показано в роботах інших дослідників і підтверджено результатами обробки отриманих в дослідженнях рядів даними даний ряд не містить циклів в повному розумінні цього терміну, а лише подібні траєкторії, які називають квазіциклами. В даному підході квазіциклом є опукла траєкторія, початок і кінець якої знаходяться в околі найменш можливого радіусу.
15.5. Виділення квазіциклів
138
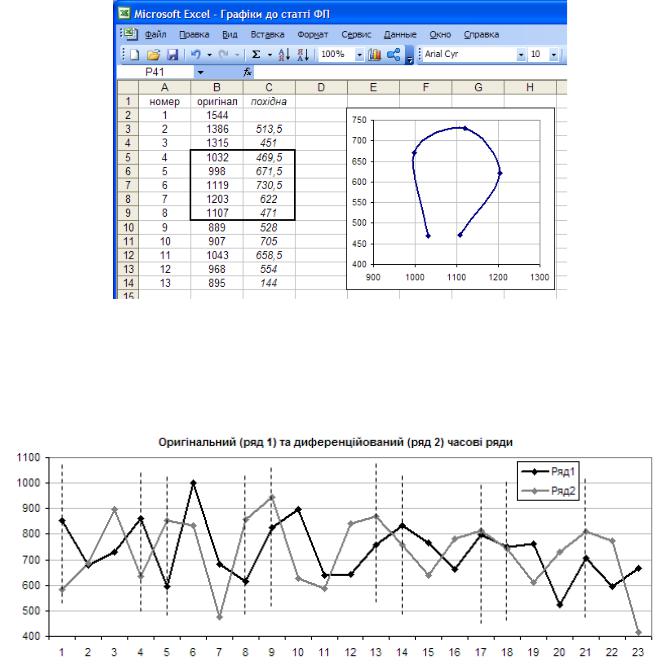
Розбиття фазового портрету на квазіцикли можна здійснити візуально, використовуючи зображення фазового портрету побудованого на перших чотирьох парах значень – значення оригінального ряду та відповідного йому значення диференційованого. Пересуваючи таке вікно і змінюючи його розмір необхідно добитися максимальної замкненості контуру квазіциклу за мінімальної кількості вузлів як показано на рис. 15.7. В стовпчиках В і С знаходяться відповідно оригінальні та диференційовані значення. У виділеному прямокутнику в стрічках дано координати зображеного справа квазіциклу. Зауважимо, що перша і остання пара координат у прямокутнику є є найбільш близькими за значеннями. С5 і С9 є дуже близькими, тому на графіку початкова і кінцева точки циклу є практично на одному рівні – різниця між їхніми значеннями дуже мала, в той же час значення В4 і В8 знаходяться на значно більшій віддалі. Хоча такий спосіб вимагає багато ітерацій він практично забезпечує мінімальну кількість пар координат, які не включені в квазіцикли, принаймні для отриманих рядів.
Рис. 15.7. Розбиття фазового портрету на квазіцикли.
Іншим способом розбиття фазового портрету на квазіцикли, який можна використати як попереднє розбиття є виділення квазіциклів на графіку зіставлених оригінального і диференційованого рядів, як це показано на рис. 15.8.
Рис. 15.8. Виділення квазіциклів. Ряд 1 – оригінальні дані, ряд 2 – диференційовані дані, штриховими лініями виділені квазіцикли.
139
Основними умовами для виділення квазіциклів є такі:
-мінімальна кількість вузлів – чотири;
-значення початкового і кінцевого рівнів, як оригінального так і диференційованого рівнів повинні бути близькими, тобто різниця між ними має бути мінімальною для даного фрагмента ряду (умова необхідна, але недостатня);
-за умови виконання п.1 різниці між значеннями початкових та кінцевих рівнів для обох рядів мають бути мінімальними.
В зв’язку з тим, що в результаті чисельного диференціювання отримані значення коливаються відносно нуля, тобто є від’ємними та додатними. Для зіставлення обох рядів необхідно «підняти» диференційовані значення, тобто: виділити тренд оригінального ряду і до нього додати диференційовані значення або визначити середнє оригінальних значень і додати його до диференційованих. Перший спосіб застосовується, якщо оригінальний ряд має явно виражений нелінійний тренд, другий – коли ряд практично стаціонарний.
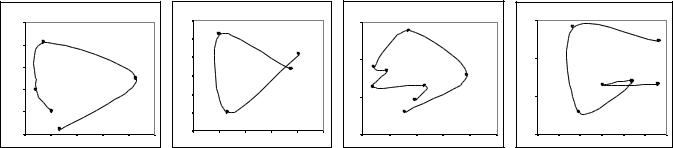
Виділені квазіцикли майже всі, мають вигляд зображений на рис. 15.9. Вони можуть мати видовжену або округлу форму, різні розміри, різну локалізацію початкових і кінцевих точок. Квазіцикли, в загальному, мали такий вигляд:
-початкова і кінцева точки квазіциклу знаходяться на мінімально можливій відстані, такій, що заміна їх на сусідні, в ту чи іншу сторону, веде до збільшення цієї відстані;
-з’єднуючі відрізки або згладжуючі лінії можуть перетинатися, проте мають забезпечити вимоги з попереднього иункту;
-квазіцикли можуть містити артефакти у вигляді петель, заглиблень тощо;
-відповідати рухові за або проти годинникової стрілки.
|
11-й квазіцикл Оп-3 |
|
|
||
1200 |
|
|
|
|
|
1000 |
|
|
|
|
|
800 |
|
|
|
|
|
600 |
|
|
|
|
|
400 |
|
|
|
|
|
200 |
|
|
|
|
|
600 |
800 |
1000 |
1200 |
1400 |
1600 |
|
1-й квазіцикл Оп-10 |
|
|||
800 |
|
|
|
|
|
700 |
|
|
|
|
|
600 |
|
|
|
|
|
500 |
|
|
|
|
|
400 |
|
|
|
|
|
300 |
|
|
|
|
|
200 |
|
|
|
|
|
600 |
700 |
800 |
900 |
1000 |
1100 |
|
2-й квазіцикл Оп-10 |
|
|
||
800 |
|
|
|
|
|
600 |
|
|
|
|
|
400 |
|
|
|
|
|
200 |
|
|
|
|
|
500 |
600 |
700 |
800 |
900 |
1000 |
Рис. 5. Вигляд квазіциклів.
|
19-й квазіцикл Оп-8 |
|
|
|||
500 |
|
|
|
|
|
|
400 |
|
|
|
|
|
|
300 |
|
|
|
|
|
|
200 |
|
|
|
|
|
|
300 |
350 |
400 |
450 |
500 |
550 |
600 |
Квазіцикли, отримані в результаті розбиття фазового портрету мають такі характеристики: кількість вузлів – точок фазової площини, що утворюють даний квазіцикл, розмір мінімальної прямокутної області покриття квазіциклу, координати центру цієї області, півпериметр області покриття, її площі та орієнтації. Ці характеристики дають підстави для інтерпретації та побудови моделі динамічної структури індивідуального часового ряду, а відтак і ідентифікувати операторський персонал.
Квазіцикли не обов’язково слідують один за одним і відстань між ними може бути в декілька послідовних рівнів.
Розбиття часового ряду на квазіцикли показує, що квазіцикли переважно містять від 4 до 8 точок, які називають вузлами. Фактично точки з’єднуються прямими відрізками, проте для кращої візуалізації їх згладжують або апроксимують сплайнами. Для ідентифікації індивідуальних часових рядів використовують діаграми (гістограми) кількості вузлів, зображені на рис. 15.10. Область покриття є прямокутною і подає габаритні розміри даного квазіциклу.
140
