
ms_lec
.pdf
У більшості випадків задачі моделювання з використанням звичайних диференціальних рівнянь зводяться до такого:
-проводиться докладний аналіз умови задачі, будується блок-схема, яка пояснює її суть, вивчається онтологія її змісту;
-складається диференціальне рівняння досліджуваного процесу, об’єкта, явища чи моделі і визначається його тип та метод розв’язування;
-шукаються загальний та частинний розв’язки та визначаються другорядні параметри з використанням додаткових умов;
-встановлюється загальний закон процесу, чисельно визначаються значення шуканих величин та характеристик;
-проводиться аналіз отриманих результатів та адекватності вихідних положень поставлений задачі.
Найбільш практичним в цьому плані є докладний аналіз вже відомих моделей на предмет пошуку відповідних аналогів поставленій задачі.
11.3. Задачі, що призводять до звичайних диференціальних рівнянь
Більшість законів природи мають диференційний характер - вони пов'язують нескінченно малі зміни розглянутих величин. Наприклад, основний закон динаміки
dp Fdt
пов'язує нескінченно мала зміна імпульсу dp з силою F, що діє в перебігу нескінченно малого інтервалу часу dt. Можна сказати, що сила - це швидкість зміни імпульсу:
F ddtp .
В останньому співвідношенні похідна вектора обчислюється як вектор з похідних:
dp |
|
d |
|
|
|
|
p |
p |
2 |
|
p |
|
|
|
|
|
p , p |
2 |
, p |
|
1 |
, |
|
, |
3 |
. |
|
|
|
|
|
|
|
||||||||
dt |
|
dt |
1 |
3 |
|
|
dt |
dt |
|||||
|
|
|
|
dt |
|||||||||
Виведення інтегральних співвідношень (співвідношень, що зв'язують кінцеві зміни величин) на підставі диференціальних законів виконується на основі результатів теорії диференціальних рівнянь.
Приклад 1. Рух у в'язкому середовищі. Нехай частинка постійної маси падає під дією сили тяжіння, причому сила опору Fr, що діє на частку з боку зовнішнього середовища, пропорційна швидкості і протилежна їй за напрямком:
Fr kv , k 0 ,
де k 0 - постійний коефіцієнт, що характеризує властивості середовища.
Знайдемо залежність, за якою змінюється швидкість частинки. Згідно з основним законом динаміки
m ddtv Fg Fr ,
де m - маса частинки, t - час, Fg - сила тяжіння, Fr - сила опору. Це векторне рівняння рівносильне системі з трьох скалярних рівнянь, вид якої залежить від вибору системи координат. Направимо вісь Ox вздовж напрямку руху (вертикально вниз). Тоді
Fg mgi , Fr kvi ,
де v - модуль швидкості. У системі залишається одне рівняння:
m |
dv |
mg kv . |
(1.1) |
|
dt |
||||
|
|
|
При вирішенні завдання не вдалося безпосередньо знайти закон, що зв'язує незалежну змінну - час t - і шукану функцію – швидкість v t ; був лише встановлений зв'язок між шуканою
функцією і її похідною. Співвідношення, подібні (1.1), називають диференціальними рівняннями. Можна переконатися, функція
91
v Ce |
k |
|
|||
|
t |
mg |
|
||
m |
(1.2) |
||||
k |
|||||
|
|
|
|
||
при будь-якому C const є рішенням рівняння (1.1). Дійсно, підстановка (1.2) в (1.1) дає
|
|
|
|
dv |
|
|
|
|
|
k |
e |
k |
t , |
|
|
|
|
|
|
|||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
dt |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
k |
t |
|
|
|
|
|
|
|
|
|
|
|
k |
t |
|
|
|
|
|||
m |
Ck |
m |
mg k |
|
|
|
m |
|
mg |
, |
||||||||||||||
|
e |
|
|
Ce |
|
|
|
|||||||||||||||||
m |
|
|
k |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
t |
|
|
|
|
|
|
|
k |
t |
|
|
|
|
||
|
|
Cke |
m |
Cke |
m |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||||
рівняння (1.1) перетворилося в тотожність.
В розв’язок (1.2) входить довільна постійна C. Для визначення цієї постійної необхідна додаткова інформація - початкова умова - значення швидкості в початковий момент часу:
v 0 v0 .
Підставляючи початкову умову у вирішення (1.2), отримаємо
|
v Ce |
k |
0 |
mg |
|
|
|
|||
|
|
, |
|
|||||||
|
m |
|||||||||
|
|
|||||||||
|
0 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v0 |
C |
mg |
, |
C v0 |
|
mg |
. |
|||
k |
|
|||||||||
|
|
|
|
|
|
|
|
k |
||
Шукана залежність швидкості від часу приймає вигляд
|
|
|
mg |
|
k |
t |
|
mg |
|
|
|
|
|
|
|
|
|
||||||
v v |
0 |
|
|
e |
|
m |
|
|
. |
(1.3) |
|
|
|
||||||||||
|
|
k |
|
|
|
|
k |
|
|
||
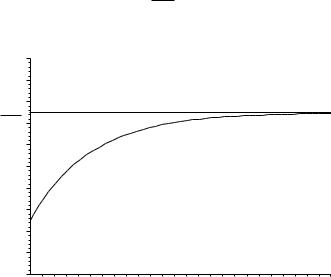
Таким чином, при русі частинки в середовищі з опором швидкість зростає від початкового значення v v0 , асимптотично наближаючись до значення
v mgk ,
при якому модуль сили опору збігається з модулем сили тяжіння (рис. 1.1).
v |
v mg |
k |
v t |
v v0 |
t |
Рис. 1.1. Залежність швидкості від часу при русі у в'язкому середовищі
Якщо опір середовища нехтує мало ( k 0 ), то (1.3) переходить в відоме рівняння кінематики:
|
|
|
k |
|
|
k |
t |
|
|
|
|
|
k |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
lim v t v |
|
lim e |
|
t |
mg lim |
1 e |
m |
v |
|
mg lim |
t |
e |
|
t v |
|
gt . |
||
0 |
m |
0 |
m |
0 |
||||||||||||||
|
|
|
|
|
||||||||||||||
k 0 |
k 0 |
k 0 k |
|
|
|
k 0 m |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
92

Приклад 2. Охолодження тіла. Нехай тіло, що має температуру 0 , в момент часу t0 0 поміщено в середовище з температурою e 0 . Потрібно знайти закон t зміни температури
тіла.
Відомо, що швидкість охолодження тіла пропорційна різниці його температури і температури навколишнього середовища:
|
d |
k e |
, k |
0 , k const . |
||||||||||||||
|
|
|
||||||||||||||||
|
dt |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Можна перевірити, що за будь-якого C const функція |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
e |
Ce kt |
|
|
|
|
||||||
задовольняє отриманому рівнянню. Постійна C може бути знайдена з початкової умови 0 0 : |
||||||||||||||||||
|
|
0 |
|
e |
Ce k 0 , C |
0 |
|
e |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Остаточно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
t |
e |
|
0 |
|
e |
e kt . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тут, як і в попередньому прикладі, шукана величина - температура тіла - асимптотично наближається до температури навколишнього середовища.
Приклад 3. Вільні коливання. Нехай частинка рухається вздовж осі Ox під дією квазіпружної сили, спрямованої до положення рівноваги і пропорційної зміщенню. Якщо абсциса положення рівноваги збігається з початком координат, то проекція сили на вісь Ox дорівнює
Fx kx ,
де k - додатна константа.
Знайдемо залежність координати від часу. З основного закону динаміки:
md 2 x kx , dt2
|
d 2 x |
|
k |
x 0 . |
(1.4) |
|
dt2 |
|
|||
|
|
m |
|
||
Можна переконатися, що будь-яка функція виду |
|
|
|
|
|
x t Asin t 0 , |
(1.5) |
||||
де A і 0 - довільні постійні, є розв’язком диференціального |
рівняння (1.5). Постійну A |
||||
називають амплітудою, а постійну 0 - початковою фазою коливань. Амплітуда і початкова фаза
визначаються положенням і швидкістю частки в початковий момент часу. Постійна
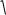
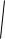 mk ,
mk ,
квадрат якої є повертаючою силою на одиницю зсуву і одиницю маси, називається круговою частотою. Залежність (1.5) зображена на рис. 1.2.
93

A |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
x t Asin |
|
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
A 0 |
|
|
2 |
3 |
t |
4 |
|
|
|
|
|
|
Рис. 1.2. Залежність координати від часу при вільних коливання
Приклади.
Хімія. У резервуарі мається 100 літрів розсолу, що містить 10 кг розчиненої солі. Кожну хвилину 2 літри розсолу випливає з резервуара, а 3 літри прісної води притікає в нього. Перемішування зберігає однакову концентрацію солі в резервуарі. Скільки солі залишиться в резервуарі через годину?
Складання рівняння. Позначимо через |
x кількість солі в резервуарі, |
через |
t - час, що |
|||||||||
відраховується від початкового моменту у хвилинах. |
|
|
|
|
||||||||
За проміжок часу dt з резервуару виходить dx кг солі [адже величина x |
(ікс) |
є спадною |
||||||||||
функцією часу, значить, dx - від’ємна величина, а dx - додатна]. |
|
|
|
|||||||||
Щоб скласти рівняння, обчислимо спад солі іншим шляхом. В момент t |
в резервуарі знаходиться |
|||||||||||
(100+ t ) літрів рідини (притекло 3 t |
літрів і витекло 2 t ), а в ній розчинено x кг солі. Значить, в |
|||||||||||
одному літрі розсолу міститься |
|
x |
|
|
кг солі. За час |
dt з резервуара витікає 2 dt літри розсолу, |
||||||
|
|
|
|
|||||||||
100 |
t |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
|
|
|
|
|
||
значить, кількість солі зменшиться на |
|
|
2dt |
кг. Отримуємо диференціальне рівняння |
||||||||
100 t |
||||||||||||
|
|
|
|
|
dx |
2xdt |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
100 t |
|
|
|
|
||
Електродинаміка. Ізольованому провіднику |
надано заряд |
q0 100Кл . |
Внаслідок |
|||||||||
недосконалості ізоляції провідник постійно втрачає свій заряд. Швидкість втрати заряду в даний момент пропорційна існуючому заряду провідника. Який заряд залишиться на провіднику після перебігу часу t 10сек , якщо за першу секунду втрачено 10 Кл .
Складання рівняння. Припустимо, що в момент часу t заряд провідника дорівнює q q t . Швидкість втрати заряду в цей момент дорівнює dqdt . Так як ця швидкість пропорційна
заряду q , то отримаємо таке диференціальне рівняння цього процесу:
dqdt k q ,
де k - коефіцієнт пропорційності.
94
Ядерна фізика. Швидкість розпаду радію в кожен момент часу прямо пропорційна його масі. Визначити, який відсоток маси m0 радію розпадеться через 200 років, якщо відомо, що
період напіврозпаду радію (період часу, після закінчення якого розпадається половина початкової маси радію) дорівнює 1590 років.
Складання рівняння. Швидкість розпаду радію вимірюється його кількістю, що розпалися
в одиницю часу. За малий проміжок часу |
t , що минув з деякого моменту часу |
t , кількість |
розпався радію рівна km t , де m - |
кількість радію в даний момент, k - |
коефіцієнт |
пропорційності. Ця ж кількість, взята зі знаком «-» (маса убуває), рівна приросту маси за час t :
m km t . |
(1) |
|
Ділимо обидві частини рівності (1) на t і переходимо до границі при t 0 . Тоді: |
|
|
lim |
m km . |
(2) |
t 0 |
t |
|
Таким чином, рівність (2) являє диференціальне рівняння з відокремлюваними змінними.
Теоретична механіка. Проходячи через ліс і відчуваючи опір дерев, вітер втрачає частину своєї швидкості. На нескінченно малому шляху ця втрата пропорційна швидкості на початку цього шляху і його довжині. Знайти швидкість вітру, що пройшов у лісі 150 м, знаючи, що до входження
в ліс початкова швидкість вітру V0 12м / с ; після проходження шляху S = 1м, швидкість вітру зменшилася до величини V1 11,8м / с .
Складання рівняння: Нехай на відстані S від початку лісу швидкість вітру дорівнює V , втрата швидкості на шляху dS дорівнює dV (процес регресний, сповільнюваний). Ця втрата
пропорційна V , і тому диференціальне рівняння процесу прийме вигляд: dV c e kS , де c – коефіцієнт пропорційності.
Біологія, процеси приросту. Нехай колонія живих організмів знаходиться в сприятливих умовах, завдяки чому народжуваність вище, ніж смертність, причому, простір, займане колонією, і харчові ресурси вважати необмеженими. Припустимо також, що хижаків, що харчуються організмами даної колонії, немає. Знайти закон зміни чисельності організмів в залежності від часу, якщо при t 0 їх число дорівнювало y0 .
Складання рівняння. будемо вважати, що швидкість зміни чисельності організмів
пропорційна до цієї чисельності і - коефіцієнт пропорційності: V y . |
||
Так як V y , |
то чисельність y організмів у колонії в момент часу t задовольняє рівнянню |
|
y y . Звідси |
dy |
y |
|
||
|
dt |
|
Розчинення речовини. Речовина A розкладається на дві речовини X і Y зі швидкістю |
||
утворення кожної з них, пропорційною кількості нерозчиненої речовини. Знайти закон зміни
кількостей x |
і |
y речовин X і Y в залежності від часу t , якщо при t 0 маємо |
x y 0 , а через |
||||||||
годину x |
a |
, |
|
y |
3a |
, де a - початкова кількість речовини A . |
|
||||
|
|
|
|||||||||
8 |
|
|
|
|
|
|
8 |
|
|
||
Складання рівняння. У момент часу t кількість нерозчиненої речовини A рівна a x y . |
|||||||||||
З умови задачі будемо мати систему |
|
||||||||||
|
|
|
dx |
|
k (a x y) , |
|
|||||
|
|
|
|
|
|||||||
|
|
|
dt |
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
dy |
k |
|
(a x y) . |
|
||||
|
|
|
|
2 |
|
||||||
|
|
|
dt |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
95
Механіка. Човен сповільнює свій рух під дією опору води, який пропорційний квадрату швидкості човна. Початкова швидкість човна 3 м / сек , а його швидкість через 4 сек складає
1 м / сек .через який час швидкість човна зменшиться до 1см / сек .
|
|
Складання рівняння. Згідно з другим законом Ньютона |
ma F , де m – маса човна, |
|||
a |
dv |
– його прискорення (похідна швидкості |
v t за часом t , F |
– сила опору води. За умовою |
||
dt |
||||||
|
|
|
|
|
||
задачі F kv2 . Отже маємо таке диференціальне рівняння: |
|
|||||
|
|
m |
dv |
kv2 . |
|
|
|
|
dt |
|
|||
|
|
|
|
|
||
Гідродинаміка. Циліндричний резервуар висотою 6 м і діаметром основи 4 м поставлено вертикально і наповнено водою. За який час вода, що заповнює цей резервуар витече з нього через круглий отвір радіусом 1/12 м , зробленому в дні резервуара?
Складання рівняння. Для розв’язку поставленої задачі треба скористатися формулою
Бернуллі, яка визначає швидкість v |
(в м/с) витікання рідини |
з отвору в |
резервуарі. Що |
||
|
рівня рідини, тобто v |
|
|
|
– постійний |
знаходиться на h м нижче вільного |
|
2gh , де |
|||
(безрозмірний) коефіцієнт, який залежить від властивостей рідини (для води 0.6 ), а g 9.8 м/с.
Нехай через t с після початку витікання води рівень решта води в резервуарі став рівним h м, і за час dt знизився ще на dh м ( dh 0 ). Тоді об’єм води, яка витекла за нескінченно малий проміжок часу dt можна визначити двома способами.
З однієї сторони цей об’єм dw є рівний об’єму циліндричного шару з висотою dh і
радіусом r основи резервуару r 2м . Таким чином, dw r2 dh r2dh .
З другої сторони, цей об’єм рівний об’єму циліндра, основою якого є отвір в дні резервуару, а висота рівна v dt , (де v – швидкість витікання). Якщо радіус отвору рівний ( 1/12 м ), то
dw 2vdt 2 
 gh dt .
gh dt .
Прирівнюючи ці два вирази, які відповідають одному і тому ж об’ємові води отримаємо таке рівняння
r 2dh 2 |
|
dt . |
|
|
|
|
gh |
|
|
|
|||
Механіка. Тіло масою m падає з деякої висоти без початкової швидкості. Під час падіння |
||||||
тіло долає опір повітря, який пропорціональний квадрату швидкості тіла. |
|
|
|
|||
Складання рівняння. Введемо позначення: нехай s – пройдений тілом шлях, |
v |
ds |
– |
|||
dt |
||||||
|
|
|
|
|
||
швидкість, |
a |
d 2s |
– прискорення. На тіло діють сили: його вага P mg (в напрямку його руху) і |
|||||||||
dt2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
ds 2 |
|
|
|
|
|||
опору повітря F kv |
|
k |
|
(проти напрямку руху). |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
dt |
|
|
|
|
|||
На основі другого закону Ньютона приходимо до такого диференціального рівняння руху |
||||||||||||
тіла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ma P kv2 , |
|
|||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2s |
ds 2 |
|||
|
|
|
|
|
|
|
m |
|
mg k |
|
. |
|
|
|
|
|
|
|
|
dt2 |
|
||||
|
|
|
|
|
|
|
|
dt |
||||
96
МОДЕЛЮВАННЯ СИСТЕМ
ЛЕКЦІЯ 12
МОДЕЛЮВАННЯ ВИПАДКОВИХ ПОДІЙ
Приведені основні засади та методи моделювання випадкових подій. Розглянуто методи отримання псевдо випадкових чисел та використання методу Монте-Карло. Подано методи моделювання випадкових подій, групи випадкових подій. Дано формули для моделювання псевдовипадкових величин з заданим законом розподілу методом оберненої функції. Приведені методи моделювання дискретних та неперервних випадкових величин.
12.1. Засади моделювання (розігрування) випадкових величин
Моделювання випадковості з допомогою комп'ютера має величезну сферу застосувань. Майже кожна імітація розгортання подій в часі, яку відтворюють з допомогою комп'ютера,використовує елемент випадковості. З допомогою так званого генератора випадкових чисел, який присутній майже у всіх спеціалізованих програмних продуктах, імітують рух молекул в складних середовищах, вивчаються виробничі процеси, економічні і фінансові ситуації, досліджуються екологічні процеси і багато інших, явищ, систем, процесів.
В теорії ймовірностей реалізацію деякого комплексу умов називають випробуванням. Результат випробування, зареєстрований як факт, називають подією.
Випадковою називають подію, яка в результаті випробування може настати, а може і не настати (на відміну від достовірної події, яка в результаті реалізації даного комплексу умов настає завжди, і неможливої події, яка при реалізації даного комплексу умов не настане ніколи).
Вичерпною характеристикою випадкової події є ймовірність її настання. Прикладами випадкових подій є відмови в економічних системах, обсяги продукції, що випускається кожним підприємством в кожен день, вихід з ладу обладнання, неочікувана зустріч з давно небаченим знайомим, виграш в лотереї тощо.
Сучасні комп’ютери дозволяють легко отримувати так звані псевдовипадкові числа, які практично повною мірою застосовують замість випадкових чисел. Це призвело до широкого впровадження методу в різні галузі науки і техніки, наприклад статистична фізика, теорія масового обслуговування, імітаційне моделювання, теорія ігор та ін. Метод Монте-Карло використовують для обчислення інтегралів, особливо багатовимірних, для розв'язання систем алгебраїчних рівнянь високого порядку, для дослідження різного роду складних систем автоматичного управління, економічних, біологічних і т.д.
Суть методу Монте-Карло полягає в тому, що потрібно знайти значення a деякої досліджуваної величини. Для цього вибирають таку випадкову величину X , математичне сподівання якої дорівнює a , тобто M X a . Практична реалізація цієї процедури є така: проводять n випробувань, в результаті яких отримують n можливих значень X , обчислюють їх
97
|
1 |
n |
в якості оцінки (наближеного значення) a |
|
середнє арифметичне x |
xi , і приймають x |
|||
|
||||
|
n i 1 |
|
||
шуканого числа a , тобто a a x .
Оскільки метод Монте-Карло вимагає проведення великого числа випробувань, його часто називають методом статистичних випробувань. Теорія цього методу вказує, як найбільш доцільно вибрати випадкову величину X , як знайти її можливі значення. Зокрема, розробляються способи зменшення дисперсії використовуваних випадкових величин, в результаті чого зменшується помилка, що допускається при заміні шуканого математичного очікування a його
оцінкою a . Відшукання можливих значень випадкової величини X в моделюванні називають «розігруванням випадкової величини». Викладемо лише деякі способи розігрування випадкових величин і вкажемо, як оцінити допущену при цьому помилку.
Позначимо через R неперервну випадкову величину, розподілену рівномірно в інтервалі (0; 1). Випадковими числами називають можливі значення г неперервної випадкової величини R , розподіленої рівномірно в інтервалі (0; 1).
Насправді користуються не рівномірно розподіленою випадковою величиною R , можливі значення якої, взагалі кажучи, мають нескінченне число десяткових знаків, а квазірівномірною
випадковою величиною R , можливі значення якої мають скінченне число знаків. В результаті
заміни R на R розігрується величина має не точно, а наближено заданий розподіл. Такі величини називають псевдовипадковими числами
Випадкові фактори та їх моделі. Під випадковим чинником домовимося розуміти випадкову подію, випадкову величину, багатовимірну випадкову величину, випадкову функцію однієї або декількох змінних і взагалі будь-які об'єкти, вибір яких визначається відповідними імовірнісними розподілами. Тоді під реалізацією випадкового фактора будемо розуміти сам акт
вибору, тобто статистичну вибірку одного елемента з множини, наділеної ймовірнісною мірою.
В даний час моделювання випадкових факторів виходить з того, що використовує програмно реалізований комп’ютерний генератор випадкових чисел, який є ідеальною моделлю базової випадкової величини R 0, 1 , тобто видає рівномірно розподілені і незалежні випадкові
значення ri . Це допомагає будувати моделі випадкових факторів і встановлювати їх властивості
теоретично – спираючись лише на положення теорії ймовірностей і не вдаючись до громіздких процедур статистичного тестування.
Моделювання випадкової події полягає у визначенні («розігруванні») факту її випадкового настання. Для моделювання випадкової події A , яка настає в такому дослідженні з імовірністю PA , достатньо одного випадкового, а в наукових дослідженнях переважно псевдовипадкового числа R , рівномірно розподіленого на інтервалі [0; 1]. У разі потрапляння такого R в інтервал [0; PA ], подію A вважають такою, що настала в даному дослідженні, в іншому випадку, що вона не настала в цьому дослідженні, тобто має місце умова
1, |
якщо R 0, PA , |
|
P A |
|
якщо R P , 1 . |
|
0, |
|
|
|
A |
Чим більшою є ймовірність настання модельованої події, тим частіше псевдо випадкові числа, рівномірно розподілені на інтервалі [0; 1], будуть потрапляти в інтервал [0; PA ], що й означає факт настання події у випробуванні.
Для моделювання одного з повної групи випадкових несумісних подій A1, A2 , , AN з ймовірностями настання відповідно рівними PA1 , PA2 , , PAN , також достатньо одного
псевдовипадкового числа R рівномірно розподіленого на інтервалі [0, 1].
Факт настання однієї з подій групи визначають, виходячи з умови приналежності псевдовипадкового числа R до того чи іншого інтервалу, на який розбивають інтервал [0; 1].
98
12.2. Методи моделювання подій |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Моделювання протилежних подій. |
Нехай маємо випадкові числа |
ri , тобто можливі |
|||||||||||||||||
значення випадкової величини , |
рівномірно |
розподілені |
|
в |
інтервалі |
0, 1 . |
Необхідно |
||||||||||||
реалізувати випадкову подію |
A , яка |
настає з заданою імовірністю p . Визначимо |
A як подію, |
||||||||||||||||
для якої вибране значення ri |
випадкової величини задовольняє нерівність |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
ri p . |
|
|
|
P A 1 p . |
|
(1) |
|||||
|
|
|
|
|
|
|
ri p . |
|
|
|
|
|
|||||||
Протилежна подія A полягає в тому, |
що |
Тоді |
|
|
|||||||||||||||
Процедура моделювання полягає у виборі значень ri і порівнянні їх з p . Якщо умова (1) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
виконується, то результатом випробування є подія A , інакше A . |
|
|
|
|
|||||||||||||||
Моделювання дискретної випадкової величини. |
Для |
того |
щоб змоделювати дискретну |
||||||||||||||||
випадкову величину X , задану законом розподілу |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
X |
|
x1 |
|
x2 |
|
|
|
|
|
xn |
|
|
|
|||||
|
P |
|
p1 |
|
p2 |
|
|
|
|
|
pn |
|
|
|
|||||
потрібно:
1) розбити інтервал 0, 1 на n окремих інтервалів:
1 0 p1,
2 p1 p1 p2 ,
n p1 p2 pn 1 1.
2)вибрати випадкове число r j .
|
Якщо випадкове число |
r j потрапляє в окремий інтервал |
i , |
то розігрувана величина |
|||||||||
приймає можливе значення xi . |
|
|
|
|
|
|
|
|
|
|
|
||
|
Моделювання повної групи подій. |
Нехай A1, A2 , , |
An |
– |
повна |
група подій, які |
|||||||
настають з ймовірностями p1, |
|
p2 , , pn |
відповідно. Моделювання повної групи несумісних |
||||||||||
подій |
можна звести |
до розігрування дискретної |
випадкової |
величини |
X |
з таким |
законом |
||||||
розподілу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
1 |
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
p1 |
p2 |
|
|
|
pn |
|
|
|
|
|
Правило: для |
того щоб змоделювати випробовування, в |
кожному |
з яких настає |
одна з |
||||||||
подій |
A1, A2 , , An повної |
|
групи подій, що настають з |
ймовірностями p1, p2 , , pn |
|||||||||
відповідно, достатньо розіграти дискретну випадкову величину з таким законом розподілу: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
1 |
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
p1 |
p2 |
|
|
|
pn |
|
|
|
|
Якщо у випробуванні величина X |
прийняла можливе значення xi , то настала подія |
Ai . |
|||||||
Моделювання незалежних подій. |
Нехай незалежні події A і B настають з ймовірностями |
||||||||
|
|
|
|
|
|
|
|||
p A і pB . Можливими наслідками сумісних випробувань будуть події AB, AB, AB, AB |
з |
||||||||
ймовірностями pA pB , 1 pA pB , pA 1 pB , 1 pA 1 pB . |
|
||||||||
В моделюванні випробувань можна використати два варіанти розрахунків:
99

1)послідовну перевірку умови (1);
2)визначення одного з результатів AB, AB, AB, AB шляхом жеребкування з
відповідними ймовірностями.
Для першого варіанту необхідна пара чисел xi , для виконання умови (1). В другому варіанті необхідне одне число xi , але порівнянь може вимагатися більше.
Моделювання залежних подій. У практиці імітаційних досліджень часто виникає необхідність моделювання залежних подій, для яких ймовірність настання однієї події виявляється залежною від того, чи настала або не настала інша подія. В якості одного з прикладів залежних подій наведемо доставку вантажу споживачеві у двох випадках:
1)коли маршрут руху відомий і був постачальником додатково уточнено,
2)коли уточнення руху вантажу не проводилося.
Зрозуміло, що ймовірність доставки вантажу від постачальника до споживача для
наведених випадків буде різною. |
|
|
|
|
|
|
|
|
|
|
|||||
|
Нехай події A і B є залежними і настають з ймовірностями |
p A і |
pB . Нехай задана умовна |
||||||||||||
імовірність |
P B | A |
настання події B |
|
за |
умови, |
що |
подія A |
відбулася. |
З |
послідовності |
|||||
випадкових |
чисел |
xi вибирають |
число xm , |
яке |
задовольняє умову |
xm p A . Якщо ця |
|||||||||
нерівність справджується, то настала подія |
A . Далі з сукупності чисел xi вибирають наступне |
||||||||||||||
число xm 1 |
і перевіряють умову xm 1 P B | A . Тут можливими результатами випробовування є |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB, AB . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Якщо умова |
xm p A не виконується, то настає подія A . |
Для випробування, зв'язаного з |
||||||||||||
подією B , необхідно визначити імовірність: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
P B | |
|
|
P B P A P B | A |
. |
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 P A |
|
|
|
|
|||
|
Виберемо з |
сукупності xi |
|
число |
xm 1 і перевіримо |
справедливість умови |
|||||||||
xm 1 P B | A . В залежності від того, виконується вона чи ні, отримаємо результати випробувань
AB або AB .
Існують два алгоритму моделювання залежних подій. Один з них умовно можна назвати «послідовним моделюванням», інший - «моделюванням після попередніх розрахунків».
Моделювання неперервної випадкової величини.
Правило 1. Для того щоб змоделювати (розіграти) |
можливе значення xi неперервної |
||
випадкової величини X , знаючи її функцію розподілу F x , |
треба вибрати випадкове число ri , |
||
прирівняти його до функції розподілу і розв'язати відносно xi |
отримане рівняння: |
||
F xi xi . |
|
|
|
Правило 2. Для того щоб розіграти можливе |
значення xi неперервної випадкової |
||
величини X , знаючи її щільність розподілу |
f x , треба вибрати випадкове число ri , і розв'язати |
||
відносно xi рівняння: |
|
|
|
xi |
x dx ri , |
|
|
f |
|
(2) |
|
a |
|
|
|
де a – найменше скінченне можливе значення X . |
|
|
|
Для низки законів розподілів, які |
найчастіше |
зустрічаються на практиці, отримані |
|
аналітичні розв'язки рівняння (2), приведені в таблиці 1. |
|
|
|
100
