
ms_lec
.pdf
Оцінка надійності простих систем. В якості оцінки надійності простих систем P
приймають відносну частоту
P A m A n
де n – загальне число проведених випробувань; m A – число випробувань, в яких настала подія
A .
Моделювання подій відбувається за правилом: якщо випадкове число є менше імовірності події, то це означає, що подія настала; якщо ж випадкове число більше або рівне цій імовірності, то вважають, що подія не настала.
Таблиця 1.
Формули для моделювання випадкових величин
Закон розподілу |
|
|
Щільність |
|
|
|
|
|
|
|
|
|
|
|
Формула для |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
моделювання |
|
|
|||||||||||||
випадкової величини |
|
|
розподілу |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
випадкової величини |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Експоненціальний |
f x e x |
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
1 |
ln ri |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
|
a 1 |
|
|
|
x |
|
a |
|
|
|
|
|
|
a |
|
|
|
|||||||
|
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вейбула |
|
|
|
|
|
|
|
exp |
|
|
|
|
|
|
|
|
|
xi |
b ln ri |
|
|
|
||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ln 1 r |
|
|
|||
Гамма-розподіл |
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f x e |
|
|
|
x |
|
|
|
|
|
|
|
|
|
i |
|
j |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
12 |
|
|
|
||
Нормальний |
f x |
|
|
|
|
exp |
x a |
|
|
xi |
x |
r j 6 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|||||||
Параметри гама-розподілу обчислюють за такими формулами:
|
x |
; |
|
x 2 |
. |
2 |
|
||||
|
|
|
2 |
||
Моделювання випадкових подій. Під час статистичного моделювання дослідник має справу з реалізацією випадкових подій. Моделювання випадкової події полягає у відтворенні появи або не появи випадкової події відповідно до заданої ймовірності.
Нехай є випадкові числа xi , тобто можливі значення випадкової величини, рівномірно розподіленої в інтервалі 0, 1 . Необхідно відтворити випадкову подію А, яка наступає із заданою ймовірністю р. Визначимо подію А, як подію, для якої обране значення випадкової величини X задовольняє нерівності xi p .
Тоді ймовірністю події А буде
|
|
|
|
|
p |
p |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
P A f x dx |
|
|
|
dx p . |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
0 |
|
||||||||
|
|
|
0 |
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
полягає в тому, що xi p . Тоді P |
|
1 p . |
||||||||
Протилежна подія |
A |
A |
||||||||||||
Процедура моделювання в цьому випадку полягає у виборі реалізацій випадкової величини |
||||||||||||||
xi та порівнянні їх з |
p . При цьому, якщо умова xi p виконується, |
то має місце подія А, інакше |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подія – „не А” – A . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Моделювання |
повної групи несумісних |
подій |
А1, А2,..., Аn, |
ймовірності яких Р(Аі)=pі; |
||||||||||
( i 1, 2, , n ) можна звести до моделювання дискретної випадкової величини Y, що має закон розподілу Р(yi)= P(Ai)=pі.
101
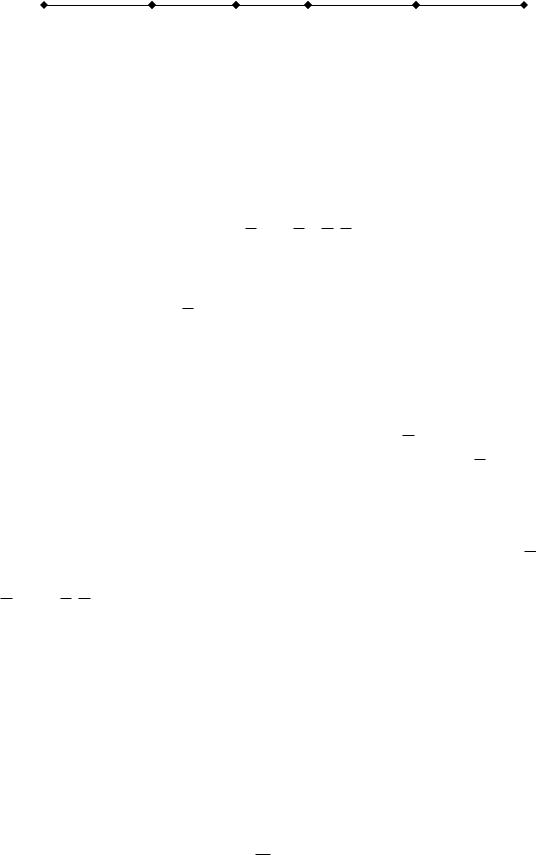
Під час практичної реалізації даного способу на одиничному відрізку числової осі відкладають інтервали і=рi (рис. 3.4).
1 |
2 |
3 |
|
... |
n |
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
Рис. 12. 1. |
|
|
|
|
Генерують рівномірно розподілене на інтервалі [0, 1] випадкове число j і перевіряють |
|||||||
умову |
|
|
|
|
|
|
|
|
|
k 1 |
|
k |
|
|
|
|
|
pi |
j |
pi |
|
|
|
|
|
i 1 |
|
i 1 . |
(12.1) |
||
У разі виконання умови (12.1) вважають, що під час випробування настала подія Аk. Під час моделювання різних систем часто необхідно здійснювати випробування, результат яких є складною подією, що залежить від двох або більше простих подій. Нехай, наприклад, незалежні події А та В мають ймовірності настання рА та рВ. Можливими результатами сумісних випробувань
в цьому випадку будуть події АВ, A В, А B , A B із ймовірностями рАрВ, (1 - рА)рВ, рА(1-рВ). Ці чотири події утворюють повну групу несумісних подій і під час моделювання можна скористатися алгоритмом для моделювання повної групи незалежних подій.
Під час використання другого способу моделювання спочатку треба визначити умовні
ймовірності Р(В/А) та Р(В/ A ), а потім розігрувати факт появи кожної з сумісних подій окремо. Наприклад, нехай задана умовна ймовірність Р(В/А) настання події В за умови, що подія А
відбулася. Із послідовності випадкових чисел x обирається чергова величина хk i перевіряється нерівність хk< рА. Якщо ця нерівність виконується, то подія А настала. Для випробування, пов’язаного з подією В, використовується ймовірність Р(В/А). Із сукупності чисел xi береться наступне число хk+1 i перевіряється умова хk+1≤ Р(В/А). Залежно від того, виконується чи ні ця нерівність, результатом випробування буде подія АВ або А B .
Якщо нерівність хk< рА не виконується, то настала подія пов’язаного з подією В, необхідно визначити ймовірність
|
|
|
P(B)-P(A)P (B/A) |
|
|
|
|
|
|
|
|
|
|
|
1 P( A) |
|
|
Р(В/ A )= |
. |
||||
|
|||||
Виберемо із сукупності xi число хk+1 і перевіримо умову хk+1≤ Р(В/ A ). Залежно від того, виконується остання нерівність чи ні, отримуємо результати випробування про настання подій
A В або A B .
12.3. Моделювання випадкових величин
Для моделювання випадкової величини із заданим законом розподілу F x P x
застосовується функціональне перетворення випадкової величини з рівномірним законом розподілу на (0, 1). Бібліотеки сучасних мов програмування мають вбудований датчик псевдовипадкових чисел, видає число U з множини 0, 1, , N 1 . З практичної точки зору,
отримані в такий спосіб випадкові величини мають рівномірний розподіл на зазначеній множині. Більшість способів отримання випадкових чисел із заданим законом розподілу вимагають використання випадкової величини з рівномірним законом розподілу на відрізку (0, 1). Наблизити
таку величину можна відношенням UN . Далі через U будемо позначати випадкову величину з рівномірним розподілом на (0, 1).
102
Для роботи з датчиком випадкових чисел необхідно вміти вибирати початкове значення псевдовипадкової послідовності. Вибір різних початкових значень дає можливість випробовувати різні відрізки послідовності псевдовипадкових чисел.
В стандартній бібліотеці мови програмування С для роботи з псевдовипадковими числами передбачені функції srand(unsigned), rand() і константа RAND_MAX. Як правило, для отримання випадкового початкового значення використовують системний годинник. Для цього один раз на початку програми здійснюють виклик srand(time(0)). Після цього виконання команди ((double) rand())/RAND_MAX видає значення випадкової величини з рівномірним розподілом на 0, 1 .
|
Моделювання дискретних випадкових величин. |
|
Моделювання дискретної випадкової |
|||||||||||||||||||||||||||
величини зі скінченним числом значень a1, a2 , , aK . Нехай |
p j – ймовірність значення а a j |
, де |
||||||||||||||||||||||||||||
j 1, 2, , K . Розіб'ємо |
відрізок |
0, 1 |
на |
напівінтервали 1 [0, p1 ) , 2 [ p1, |
p1 p2 ) , |
... , |
||||||||||||||||||||||||
K [ p1 p2 pK 1, 1] . Нехай u |
– значення випадкової величини U . Знайдемо інтервал j , |
|||||||||||||||||||||||||||||
якому належить число u . Тоді в якості випадкової величини виберемо a j . |
|
|
|
|
|
|
||||||||||||||||||||||||
|
Найпростішим прикладом такої випадкової величини є індикатор I A I A |
події |
A . |
|||||||||||||||||||||||||||
За визначенням, |
I A |
приймає |
значення 1 |
при |
A , і приймає |
значення 0 |
при |
A . |
||||||||||||||||||||||
Припускаючи, |
що |
|
ймовірність |
p A |
визначена, зможемо |
«розіграти» значення випадкової |
||||||||||||||||||||||||
величини |
I A |
в такий спосіб. Отримаємо значення u |
випадкової величини |
U . |
Якщо u p , |
|||||||||||||||||||||||||
покладемо IA 1 , інакше покладемо I A 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Для конкретних розподілів схема розбиття на підінтервали легко модифікується. |
|||||||||||||||||||||||||||||
Наприклад, |
для ряду розподілів (Пуассона та геометричного) число можливих значень лічильне. |
|||||||||||||||||||||||||||||
Зауважимо, |
що відношення k j |
|
p j |
|
для цих розподілів простим чином залежить від |
|
j . Тому |
|||||||||||||||||||||||
p j 1 |
|
|||||||||||||||||||||||||||||
немає необхідності зберігати (лічильну!) кількість точок розбиття відрізку |
0, 1 , оскільки |
|||||||||||||||||||||||||||||
можливо легко знаходити межі через рекурентне співвідношення pj k j pj 1 . |
|
|
|
|
|
|
||||||||||||||||||||||||
|
Наприклад, розглянемо розподіл Пуассона з параметром . Для |
j 1, 2, маємо: |
|
p e , |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
k j |
p j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
j |
|
e , |
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
p j 1 |
j |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j! |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нехай для означеності 1 і |
u 0.7359. |
Оскільки p |
e 1 |
0.3679 |
і u p , обчислимо |
p : |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
1 |
p1 |
p0 |
0.3679. |
|
|
Тоді |
p0 p1 |
0.7358 |
і |
u p0 p1 . |
Аналогічно, |
p2 |
p1 |
0.1839, |
|||||||||||||||||
1 |
|
|
|
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p0 p1 p2 |
0.9197. Тепер u [ p0 |
p1; p0 p1 p2 ) і, значить, 2 . |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Для геометричного розподілу функціональне перетворення може бути й іншим. Випадкова |
|||||||||||||||||||||||||||||
величина |
|
|
lnU |
|
|
має геометричний розподіл з параметром |
p . Тут означає цілу частину |
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
ln 1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
числа. Однак накладні витрати на обчислення логарифма можуть зробити такий спосіб повільним.
Моделювання неперервних випадкових величин. |
Нехай неперервна випадкова величина |
||||||
задана своєю |
щільністю розподілу |
f x п(х). |
Функція |
розподілу F x буде безперервною. |
|||
Припустимо |
додатково, |
що F x |
монотонно |
зростає |
на деякому інтервалі |
xmin , xmax , |
|
xmin xmax |
і |
постійна поза ним. Розглянемо |
функцію G x : 0, 1 xmin , xmax , |
||||
обернену до |
F x на |
x xmin , xmax . Покажемо, що випадкова величина G U |
має функцію |
||||
розподілу F x . Дійсно, |
нехай x xmin , xmax , тоді |
|
|
||||
|
|
|
P G U |
x P G U F x F x |
|
||
|
|
|
|
|
|
|
|
103

Розглянемо приклад. Нехай потрібно отримати значення випадкової величини зі змішанням показниковим розподілом, заданим функцією розподілу
|
0, |
якщо |
x , |
F x 1 e x |
якщо |
x . |
|
|
|
|
|
Знайдемо зворотну функцію. Вирішуючи рівняння y 1 e x , отримуємо:
G x ln 1 x . Зауважимо, що якщо U має рівномірний розподіл на 0, 1 , то такий же розподіл має величина 1 U . Остаточно маємо: lnU .
Такий метод працює, якщо зворотна функція G x має простий вираз. Часто це не так.
Наприклад, з однієї теореми Ж. Ліувіля випливає, що функція розподілу стандартного нормального закону
|
|
1 |
|
x |
|
|
t |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|||
2 |
|
exp |
2 |
dt |
|||||
|
|
|
|
|
|
|
|||
не виражається через елементарні функції в кінцевому вигляді, а значить, і немає можливості явно записати обернену до неї. Тому для моделювання стандартної нормальної випадкової величини застосовують спеціальні функціональні перетворення. Розглянемо два з них.
1. Нехай U1, U2, , UT – незалежні випадкові величини з рівномірним на 0, 1
розподілом. З врахуванням E U1 12 , D U1 121 , по центральній граничній теоремі Ляпунова,
|
|
|
U2 |
UT T 2 |
|
|
|
|||
lim P |
U1 |
|
|
x |
||||||
|
|
|
|
|
|
x |
||||
|
|
|
|
|
||||||
|
|
T 12 |
||||||||
T |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Наприклад, при T 12 випадкова величина 0, 1 U1 U2 U12 6 має наближено
стандартний нормальний розподіл. З відомих властивостей нормального розподілу отримуємо, що випадкова величина N a, a N 0,1 має наближено нормальний розподіл з середнім a і
середньоквадратичним відхиленням (зазначені числові характеристики точні). Недоліком цього методу є погана поведінка 0, 1 «на хвостах» розподілу. Очевидно, 6 0, 1 6 , тому
значення, менші за мінус шість, і більші за шість, просто не зустрінуться.
2. Другий метод дозволяє отримувати одночасно дві незалежні стандартні випадкові
величини. Цей метод називається методом полярних координат Бокса-Мюллєра-Марсальї. Його алгоритм є таким.
Крок 1. |
Нехай U1 і U2 |
– незалежні і рівномірно розподілені на 0, 1 . Покладемо |
|||||||
V1 2U1 1, V2 2U2 1 . |
|
|
|
|
|
|
|
|
|
Крок 2. |
Обчислимо S V 2 |
V 2 . |
|
|
|
|
|
||
|
|
1 |
2 |
|
|
|
|
|
|
Крок 3. Якщо S 1, повертаємось до кроку 1. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Крок 4. |
Обчислимо V |
|
2ln S |
, |
2 |
V |
2ln S . Це необхідні нормально |
||
|
1 |
1 |
|
S |
|
2 |
S |
||
|
|
|
|
|
|
|
|||
розподілені випадкові величини.
104
МОДЕЛЮВАННЯ СИСТЕМ
ЛЕКЦІЯ 13
ПОДАННЯ СКЛАДНИХ СИСТЕМ ЧАСОВИМИ РЯДАМИ
Приведені методи подання динаміки систем експериментальними даними у вигляді часових рядів. Показано моделювання часового ряду функціями Гевісайда. Розглянуто загальні характеристики часових рядів. Для виділення тенденції використані методи ковзного середнього, експоненціального згладжування та медіанної фільтрації. В якості критерію міри згладжування використовується критерій поворотних точок.
Наукові дослідження являють собою складний, ітераційний процес, що є поєднанням теоретичних, включаючи методи моделювання, і експериментальних методів. Не применшуючи достоїнств теоретичних методів дослідження, значення експериментальних методів важко переоцінити. Тільки за допомогою експерименту можливе отримання достовірної інформації про досліджуваний об'єкт в реальному масштабі часу, після обробки якої можлива побудова його моделі. Відкриття нових ефектів, нових явищ експериментальним шляхом, які неможливо пояснити на базі існуючих теорій, стимулює розвиток фундаментальної науки. У той же час, отриманий новий теоретичний науковий результат, потребує підтвердження основних положень нової теорії, а отже потребує його експериментальної перевірки.
При проведенні експериментальних наукових досліджень дотримуються таких етапів: 1. постановки завдання досліджень в термінах предметної області;
2. побудова моделі досліджуваного об'єкта і визначення важливих інформативних
|
|
|
|
параметрів , що адекватно описують її в рамках поставленого завдання; |
|||
3. за допомогою технічних засобів |
здійснюються вимірювання, реєстрація і обробка |
||
|
|
|
|
миттєвих значень спостережуваних процесів |
X |
, t , з метою визначення вектора інформативних |
|
|
|
|
|
параметрів , що описують модель процесу; |
|
|
|
4. за результатами обробки інформації встановлюють взаємно однозначну відповідність |
|||
|
|
|
|
між векторами |
і , тобто , що використовуються для побудови шуканої моделі |
||
об'єкта;
5.виконується аналіз отриманих результатів;
6.якщо результати влаштовують – експеримент закінчено, в іншому випадку необхідно
повторити пункти 3, 4 (наприклад, точність отриманих результатів незадовільна), або пункти 2 – 4
(вектор параметрів ще не достатньо повно описує поведінку об'єкта), а іноді і пункти 1 – 4 (коли ставиться інша задача).
Треба зазначити, що завдання 1, 2 і 4, 5, як правило, вирішує фахівець даної предметної області, формулюючи та інтерпретуючи її в термінах предметної області, а 3 завдання – фахівці в галузі вимірювання і обробки вимірювальної інформації.
В результаті обробки отриманої |
інформації, абстрагуючись від конкретних фізичних |
|
|
об'єктів і вектора фізичних параметрів |
можна безпосередньо переходити до математичного |
опису досліджуваних процесів, явищ, об’єктів, ситуацій, систем. Кожне з перерахованих завдань має свої специфічні особливості.
Представлення експериментальних даних часу розпізнавання.
105
4.2.1. Характеристика експериментальних даних. Практично в кожній області існують явища, які цікаво і важливо вивчати в їх розвитку тобто в динамічному аспекті. З огляду на людино-машинний інтерфейс опрацювання зорової інформації можуть представляти інтерес взаємозалежність чинників, виражених показниками, що характеризують, наприклад, умови середовища, функціональний стан та працездатність і здоров’я людини-оператора, час розпізнавання об’єкта і т.д. Всі вони змінюються в часі. З плином часу змінюється працездатність людей, протікання того чи іншого виробничого процесу, оперативність в розпізнаванні ситуацій чи зображень. Ці зміни для будь-якої характеристики такого роду протягом визначеного часу спостережень представляють конкретними вибірковими значеннями з певною статистичною структурою та особливостями, законами розподілу та їх параметрами.
В результаті спостережень за роботою людини-оператора, переважно в спеціально спланованих і поставлених експериментальних дослідженнях її інтелектуальної діяльності отримуємо дані у вигляді множини значень деякого контрольованого показника, фіксованого протягом часу спеціально планованого експерименту або реальної діяльності на робочому місці.
Значення |
цього |
показника |
пов'язують з конкретними моментами |
часу |
ti , ti T , де |
||
T ti : ti |
ti 1, |
i |
|
– |
|
|
|
1, N |
впорядкована множина моментів часу, а |
N – |
обсяг даних, а їх |
||||
послідовність представляють часовим рядом. Під впливом різних внутрішніх і зовнішніх факторів характер траєкторії даного показника переважно змінюється, причому можуть мати місце і досить різкі і суттєві його зміни. Впорядковану в часі таку послідовність спостережень називають часовим рядом. Основною рисою, яка виділяє аналіз часових рядів з посеред інших видів статистичного аналізу, є істотність саме порядку, в якому проводяться спостереження. Якщо в багатьох задачах спостереження статистично незалежні, то в часових рядах вони, як правило, залежні, а характер цієї залежності визначається положенням спостережень в послідовності. Природа ряду і структура породжуючого ряд процесу визначають порядок і характер утвореної послідовності.
Загальний вигляд таких часових рядів та їх тенденцій, що є даними експериментальних досліджень розпізнавання людиною-оператором, пред’явлених на моніторі, зображень об’єктів заданого класу, представлено на рис.4.2. Рівні рядів відповідають часу розпізнавання об’єктів. Тривалість експерименту становила дві години, експозиція кожного зображення тривала 0.6 сек., поява зображень з об’єктами заданого класу в часі мала рівномірний розподіл в межах 50 – 150 сек.
Отримані експериментальні дані використовувались як основний вихідний матеріал для побудови одномірних моделей оперативності персоналу. Вже візуальний аналіз великої кількості часових рядів, отриманих у відповідно організованих експериментах, в яких операторам були пред’явлені послідовності однорідних за своїми характеристиками зображень об’єктів показав, що вони мають переважно специфічний вигляд і володіють наступними властивостями:
розподіл за характером їх тенденції можна поділити на два типи:
- з явно вираженим нелінійним трендом, початок якого відповідає періоду адаптації, як у випадку Оператора А, (рис.4.2);
- з відсутнім періодом адаптації і практично лінійним трендом, як у випадку Оператора Б
(рис.4.2);
мають багато рівнів, значення яких суттєво перевищують візуальний усереднений тренд, визначений при відсутності цих рівнів, а, оскільки вони більш-менш регулярно розподілені вздовж ряду, не має підстави приймати їх за помилки чи промахи, крім того, їх можна прийняти за результат індивідуальних особливостей робочих алгоритмів;
106
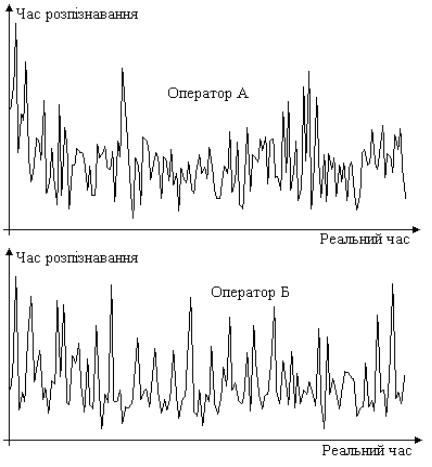
Рис.4.2. Типові часові ряди витрат часу для розпізнавання зображень.
функція щільності їх розподілу є одномодальною, асиметричною та обмеженою зліва, причому це обмеження є індивідуальним для кожного оператора і зумовлене скінченністю в часі психомоторних процесів та класом розв’язуваних задач;
загальна дисперсія рівнів рядів є значно більшою порівняно з девіацією тренду.
4.2.2. Формування часових рядів.
Модель динаміки операторської діяльності зв’язує між собою зміну таких факторів: кількісних та якісних характеристик вхідної інформації, функціонального стану оператора, часових втрат процедур розпізнавання та прийняття рішення, параметрів робочого середовища, а також моменти змін впливу не передбачуваних короткочасних або тривалих нестандартних ситуацій.
Експериментальні дослідження операторської діяльності переважно орієнтують на визначення деякого інтегрального показника, наприклад оперативності вибору і прийняття рішень
– параметра, який відноситься до конкретного оператора. Тоді, використовуючи одиничну |
||||||
функцію Гевісайда t , модель експериментальних досліджень, можна представити так. |
|
|||||
|
X xi : xi x ti , ti 0, T , i |
|
|
|
||
Нехай |
1, N |
– послідовність зображень, |
||||
представлених оператору на моніторі в моменти ti , причому |
|
|
||||
|
const, |
регулярний процес, |
|
|||
|
|
|
|
|
|
|
|
ti ti 1 |
|
|
|
|
|
|
|
випадковий процес. |
|
|||
|
prob, |
(4.1) |
||||
|
|
|
|
|
. |
|
Послідовність моментів ti пред'явлення операторові |
зображень xi на моніторі |
можна |
||||
представити зростаючою східчастою функцією |
|
|
|
|
|
|
|
|
107 |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
f1 t t ti N t t N , |
|
|
|
(4.2) |
||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
Оператор має опрацювати зображення |
xi |
за |
час |
i ti ti 1 . Позначимо |
через |
|||||
i ti i момент реалізації прийнятого оператором за час i |
рішення, причому |
ti |
i |
ti 1 . |
||||||
Послідовність моментів прийняття рішень |
відносно експонованого зображення i |
представимо |
||||||||
також східчастою функцією аналогічною до |
f1 |
t |
|
|
|
|
|
|
|
|
|
N |
|
i N t N |
|
|
|
||||
f2 t t |
|
|
|
|||||||
i 1 |
|
|
|
|
|
. |
|
|
(4.3) |
|
Різниця функцій f1 t і f2 t є потоком випадкових прямокутних імпульсів |
одиничної |
|||||||||
амплітуди, тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
f3 t f1 t f2 t |
t ti 1 N t tN |
|
|
|
||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
N |
|
|
|
|
|
N |
|
|
|
|
t i 1 |
N t N |
Ai s t i |
|
|
|
|||||
i 1 |
|
|
|
|
|
i 1 |
, |
|
|
(4.4) |
|
|
|
|
|
|
|
|
|
||
де Ai 1 – амплітуда імпульсів, |
а |
s t i |
– функція локалізації границь імпульсу на |
|||||||
часовій осі. |
|
|
|
|
|
|
|
|
|
|
Оскільки різниця t ti t i i |
визначає тривалість імпульсу не прив'язуючи |
|||||||||
його до часової осі, співвідношення f3 t можна записати як послідовність імпульсів і пауз |
|
|||||||||
|
N |
|
|
|
|
|
|
|
|
|
f4 t 1 μ τi η ti 1 τi |
|
|
|
|||||||
i 1 |
|
|
|
|
|
, |
|
|
(4.5) |
|
тут μ приймає значення 0 або 1; при |
μ 0 |
f4 t визначає сумарний час опрацювання |
||||||||
оператором наданих зображень, а при μ 1 – чистий час опрацювання.
Характер випадковості імпульсів в залежності від типу пред'явлення зображень відображений або у їх тривалості, або у моментах початку і тривалості імпульсів. Закон розподілу моментів пред'явлення імпульсів задається програмою експерименту, а розподіл їх тривалостей є індивідуальною характеристикою оператора, який розпізнає ці зображення. Вже в цьому простому випадку, використання даних (отриманих в експерименті) дозволяє отримати ряд параметрів які характеризують операторську діяльність і можуть використовуватись для атестації операторського персоналу, та робочих місць.
Оскільки заміри проводять дискретно, регулярно або в довільні визначені моменти часу, то дані представляють часовими рядами, які переважно на графіках зображають паралельними і синхронізованими в часі, де кожна реалізація відповідає за динаміку конкретного показника. Наприклад, на рис.4.3а. в часових координатах зображено послідовність пред’явлюваних операторові зображень з об’єктами пошуку з тривалістю експозиції кожного з них рівною
i ti const, причому величину ti 1 i , яка визначає час зміни зображень і визначається характеристикою системи візуалізації намагаються мінімізувати, наближаючи її до нуля. На рис.4.3а., оскільки по осях відкладено реальний час, час експозиції зображення відповідає
108
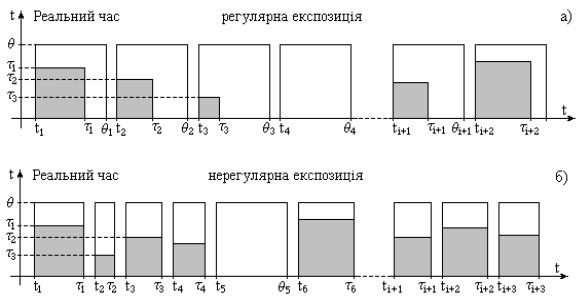
тривалості світлого імпульсу, а час розпізнавання кожного зображення, що є випадковою
величиною, яка рівна i з моменту початку експозиції i -го зображення, відповідає тривалості сірого імпульсу.
Рис.4.3. Представлення часу розпізнавання зображень.
Послідовність на рис.4.3а є регулярною, оскільки тривалість експозиції однакова, тому оператор після розпізнавання мусить чекати на наступне зображення, що призводить за певних значень часу експозиції до дискомфорту в сенсі випадкових змін нервово-напруженого стану і розслаблення, коли не вистачає часу ні на відновлення, ні на мобілізацію мислених процесів, пам’яті та уваги. На рис.4.3б. тривалість експозиції визначається часом розпізнавання, тобто
i i і моменти експозиції ti утворюють нерегулярну послідовність. Окремі світлі імпульси на рис.3а,б. означають відсутність або пропуск об’єктів пошуку. Крім того, в реальних ситуаціях появи зображень з шуканими об’єктами можуть бути не лише випадковими, але і рідкісними подіями, а це в свою чергу створює значне психологічне навантаження, зумовлене постійним підтримуванням уваги, зосередженості, мобілізації зору та пам’яті протягом кожної експозиції зображення.
4.2.3. Загальні характеристики часових рядів та їх моделей. Очевидно, що для того щоб побудувати адекватну модель операторської діяльності на підставі експериментальних даних з використанням тестових зображень необхідно вирішувати одночасно дві задачі – пряму і обернену
– побудувати модель, яка б найбільш повно, використовуючи характеристики вхідного зображення, відображала характеристики операторської діяльності і побудувати тестові зображення так щоб вони дали якомога більше потрібної інформації для побудови такої моделі. В роботі [42] запропонований підхід побудови моделі на основі часових рядів, який в даному випадку може бути представлений з несуттєвими змінами такими етапами.
1.Проводять попередній аналіз отриманих даних та додаткової інформації, здійснюють перевірку даних на аномальні значення, пропуски, метрологічну узгодженість шкал і розмірностей, визначають відповідність меті дослідження та місце в ньому майбутньої моделі, конкретизують мету побудови моделі.
2.Створюють з допомогою обчислювальної техніки відповідне програмне середовище, яке має забезпечити не лише обробку та візуалізацію даних, але і сприяти обґрунтуванню та інтерпретації отриманих результатів та побудованої моделі. В цьому плані найбільш доцільно використовувати стандартні або широко використовувані програмні пакети.
3.Враховуючи нелінійність в часових рядах з допомогою існуючих критеріїв, здійснюють вибір класів моделей-кандидатів, обчислюють і аналізують кореляційні та автокореляційні характеристики з метою визначення сили впливу і важливості різних факторів, проводять
109
спектральний аналіз для визначення коливальних складових.
4.Вибирають метод визначення параметрів моделі, зокрема коефіцієнтів тренду та чисельних характеристик випадкової складової, критерії перевірки оцінок параметрів.
5.Здійснюють перевірку побудованої моделі на адекватність.
Однією з найбільш поширених моделей часових рядів є наступна модель
|
|
n |
|
|
|
y t f t Ai sin i t i t |
|
|
|||
|
f t |
i 1 |
, |
|
|
де |
– тренд |
(характеристика тенденції), |
Ai , i , i |
– амплітуда, частота і фаза |
|
|
|
||||
циклічної компоненти, t – випадкова складова. Як правило часові ряди отримані в проведених експериментах мають дуже слабо виражену циклічну складову. А тому основна увага при побудові моделі є приділена трендові та випадковій складовій. В якості моделі тренду, який переважно є нелінійним, використовують різні аналітичні функції. Наприклад,
- поліноміальні
ft a0 a1t a2t 2 ant n ,
-з мішаними степенями [67]
ft a1t 2 a2t 1 a3t0 a4t a5t 2 ,
-логістичні [205]
f t t0 |
|
c |
|
|
|
|
|
|
|||
1 K a0 |
a1 t . |
||||
|
|
||||
В |
результаті |
елімінації тренду з часового ряду отримують елементи випадкової |
|||
компоненти, які практично мають нульове математичне сподівання та скінчену дисперсію, проте відповідність нормальному розподілу повинна бути обов’язково перевірена.
Окремі рівні часових рядів індивідуальних значень часу розпізнавання об’єктів часто мають порівняно великі значення, що є природною властивістю, обмежених мінімальним часом, психомоторних реакцій людини. Самі рівні мають асиметричний, зрізаний в області малих значень, одномодальний розподіл.
При побудові математичних моделей часових рядів, переважно з метою визначення динаміки показника, необхідно в першу чергу виділити тенденцію та відокремити її від випадкових відхилень, зумовлених різними, переважно перешкоджаючими факторами.
Дослідження часового ряду починається з його графічного представлення. При візуальному способі будується графік часового ряду, на основі якого висувається гіпотеза про його структуру, в першу чергу про форму тренду. Цей підхід дає задовільні результати при відносно монотонних тенденціях. Однак у випадку значних флуктуацій модельованого процесу можливість помилок у виборі виду функції тренда при даному підході зростає.
Методи виявлення основної тенденції розвитку досліджуваного об’єкта переважно визначаються на основі докладного вивчення фактичного розвитку його динаміки. Вони повинні узгоджуватись з результатами спостережень і статистикою емпіричного матеріалу. Ці методи мають різну логічну змістовність і тому застосовуються до часових рядів в залежності від цілей дослідження. Основна їх мета полягає в тому, щоб розкривати загальні закономірності розвитку, затушовані окремими, іноді випадковими обставинами. Проте кожен з них має свої особливості.
Для виявленні тенденції – характеру розвитку використовують процедуру згладжування часового ряду. Суть її зводиться до заміни фактичних рівнів часового ряду розрахунковими, але з меншими коливаннями, що сприяє більш чіткому проявленню тенденції та її характеру. Саме в цьому випадку, тенденцію зображають гладкою неперервною функцією, яку або її графік називають трендом часового ряду.
Метою даної роботи є ознайомлення з основними методами висвітлення тенденції поведінки досліджуваного показника, яка представлена характером його тренду, з допомогою
110
