ms_lec

яка перетворює рівняння у тотожність і має стільки довільних сталих C1, C2 , , Cn , який порядок рівняння.

Частинним розв'язком диференціального рівняння називається функція y x , яку отримують із загального розв'язку (2) шляхом надання сталим Ci , де i 1, 2, , n певних

значень.

Задача Коші – знаходження частинного розв'язку рівняння (1), який задовольняє початкові

умови:

Рівняння (1.1) є рівнянням найбільш загального вигляду і описує поведінку системи у всіх режимах. Один з окремих випадків таких режимів – це статичний режим, тобто такий режим, при якому ні вхідні, ні вихідні сигнали системи не змінюються в часі. Звичайно, це є певною ідеалізацією, яка виходить з рівняння (1.1) завдяки формальній підстановці n :

y n y n 1 y r m r m 1 r 0 .

Тоді рівняння статики прийме вигляд

Рівняння (1.3) описує статичну характеристику системи.

Розв’язок рівняння (1.1) для довільної функції F наштовхується на непереборні труднощі і є можливий тільки в деяких окремих випадках. Одним з таких окремих, але досить важливих випадків є випадок, коли функція F є лінійною функцією за своїми аргументами, тобто коли рівняння, що зв'язує вхідний сигнал r t з вихідним y t , є лінійним диференціальним рівнянням:

81

Коефіцієнти цього рівняння ai t в загальному випадку можуть залежати від часу і тоді

рівняння (1.4) описує нестаціонарну систему. Якщо такої залежності від часу немає (або вона дуже слабка) то приходимо до лінійного диференціального рівняння з постійними коефіцієнтами:

a0 y n a1 y n 1 an y an 1r m an 2r m 1 an m 1r 0 .

Останнє рівняння прийнято записувати так, щоб вихідна величина і її похідні залишалися б

рівняння типу (1.5). Нехай для деякого сталого значення входу rcm отримано рівняння статики

(1.2). Тоді розкладемо ліву частину рівняння (1.1) в ряд Тейлора (припускаючи, що таке розкладання має місце) близько точки сталого режиму і обмежимо цей ряд лінійними приростами змінних.

і перенісши доданки з вхідним впливом і його похідними в праву частину, отримаємо:

Отримане рівняння (1.7) описує ту ж саму систему, що і рівняння (1.1), але воно має такі відмінності.

По-перше, рівняння (1.7) наближене, причому це наближення тим точніше, чим менше відхилення змінних від сталих значень.

По-друге, оскільки при виведенні рівняння (1.7) використовувалося розкладання в ряд Тейлора, а така операція відноситься тільки до неперервно-диференційовних нелінійних.

Такі нелінійності називаються лінеаризованими, а нелінійні функції, що не задовольняють цій умові, називаються суттєво нелінійними.

82

По-третє, рівняння (1.7) складено відносно відхилень, а не самих сигналів. Такого роду рівняння називаються рівняннями у відхиленнях або у варіаціях.

По-четверте (і це основне), рівняння (1.7) є лінійним.

Оскільки форма рівнянь (1.7) і (1.5) збігається, тому надалі можна використовувати будьяке з них, наприклад, (1.5) маючи на увазі, що в якості змінних можуть бути і відповідні відхилення.

Запис (1.5) незручний. Зручніше записувати зв'язок між входом і виходом системи за допомогою деякого оператора, що здійснює операцію над вхідним сигналом, щоб отримати

вихідний. Для цього досить замінити i -у похідну за часом формально на si i 0, 1, 2, , при

цьому s0 1 означає відсутність диференціювання. Тоді вираз (1.5) можна переписати в такому вигляді

Дріб (1.10) носить назву передавальної функції або оператора системи. Поки будемо розглядати її як зручну форму запису лінійного диференціального рівняння (1.9).

10.2. Загальні властивості лінійних диференціальних рівнянь

Припускаючи, що вхідний сигнал r t відомий, праву частину рівняння (1.8) можна подати як f t , яку іноді називають вимушуючою функцією, і переписати рівняння (1.8) у вигляді

лінійної незалежності n розв’язків цього рівняння полягає у відмінності від нуля визначника Вронського або вронскіана:

83

де y1, , yn – розв’язки рівняння (1.12).

Загальний розв’язок рівняння (1.12) має такий вигляд:

де ci , i 1, 2, , n – довільні постійні. Рівняння (1.14) означає, що якщо відомі n розв’язків

рівняння (1.12), то довільний його розв’язок можна подати лінійною комбінацією цих n розв’язків.

Для систем з постійними параметрами існує загальний метод знаходження незалежних розв’язків однорідного рівняння. Для систем із змінними параметрами такого методу не існує. Загальне розв’язок неоднорідного рівняння (1.11) складається із суми – загального розв’язку однорідного рівняння (1.12) і будь-якого довільного (окремого) розв’язку, що задовольняє рівняння (1.11):

y t y0 t yn t

Для знаходження окремого розв’язку yp t придатний будь-який метод. Так як yp t не містить довільних постійних, то в розв’язку y t , також як і в y0 t , міститься n постійних. Для їх знаходження необхідно знати початкові або граничні умови.

10.3. Диференціальні рівняння та математичне моделювання

Поняття математичного моделювання трактується різними авторами по своєму. Ми будемо його пов’язувати з нашою спеціалізацією – прикладна математика. Під математичним моделюванням ми будемо розуміти метод дослідження процесів або явищ шляхом побудови їхніх математичних моделей і дослідження цих процесів. В основу методу покладемо адекватність між змінними складеного рівняння і досліджуваного процесу. Зрозуміло, що на практиці ці процеси не будуть абсолютно ідентичні. Але можна удосконалювати математичну модель, яка більш точно буде описувати цей процес. Треба пам’ятати, що в останньому випадку, як правило, математичні рівняння ускладнюються. А це означає, що їх моделювання на ЕОМ потребує більше часу.

Схема таких досліджень починається з постановки задачі і закінчується проведенням ефективного обчислювального експерименту. Її умови можна записати в такій формі:

а) постановка задачі; б) побудова математичної моделі та перевірка її адекватності;

в) узагальнення та теоретичне дослідження даного класу задач; г) розробка алгоритмічного забезпечення для розв'язування досліджуваних задач; д) створення програмного забезпечення; е) проведення обчислювального експерименту;

ж) впровадження цих результатів у виробництво.

Розглянемо питання використання диференціальних рівнянь в деяких предметних областях.

84

Біологія. Необхідно знайти залежність площі S молодого листка, що має форму круга,

від часу t . Відомо, що швидкість зміни площі dS в момент t пропорційна площі листка, довжині dt

його обводу та косинусу кута між падаючим на листок сонячним променем і вертикаллю листка. Маємо модель

c – довільна стала.

Диференціальні рівняння в екології. Екологія вивчає взаємовідношення людини і, взагалі, живих організмів з навколишнім середовищем. Основним об’єктом дослідження в екології є еволюція популяцій (сукупність одного виду рослин, тварин, чи мікроорганізмів, які населяють протягом тривалого часу певну територію).

Опишемо математично процес розмноження чи вимирання популяцій. Нехай x(t) –

кількісний стан популяції в момент t , A – число, яке відповідає кількості народжених, B – умираючих в одиницю часу. Тоді швидкість зміни координати x(t) задається формулою

85

Розглянемо більш детально двох видову модель «хижак-жертва», яка була побудована для виявлення коливань рибних уловів в Адріатичному морі.

Нехай x(t) – число великих риб-хижаків, y – число малих риб-жертв в момент часу t .

Тоді число риб-хижаків буде рости до того часу, поки у них буде їжа. Якщо корму не буде вистачати, то кількість риб-хижаків буде зменшуватися і тоді, починаючи з деякого моменту, буде рости число риб-жертв. Модель такого прикладу має вигляд

dx ax bxydt

, (1.7)

dy cx dxydt

де a,b, c, d – додатні константи.

В (1.7) доданок bxy виражає залежність приросту великих риб від числа малих, dxy – зменшення числа малих риб від великих.

Диференціальні рівняння закону попиту і пропозиції в економічних дослідженнях.

Попит і пропозиція – економічні категорії товарного виробництва. Попит – представлена на ринку потреба в товарах, пропозиція – продукт, який є на ринку чи може бути доставлений на нього.

Нехай p(t) – ціна, наприклад, на фрукти, dpdt – тенденція формування ціни. Тоді, як попит

так і пропозиція будуть функціями введених величин. Як показує практика, ці функції можуть бути різними. Часто попит q і пропозиція S задаються лінійними залежностями, наприклад

q 4 p 2 p 39, S 44 p 2 p 1

залежностями. Для того, щоб попит відповідав пропозиції необхідно ( p S )

Це закон зміни ціни, щоб між попитом і пропозицією була рівновага.

Диференціальне рівняння теплової магістралі. Трубопровід теплової магістралі діаметром 20 см захищений ізоляцією товщиною 10 см; коефіцієнт теплопровідності ізоляції k 0.071 Bm / м К . Температура труби 160 C ° ; температура зовнішнього покриття 30 C °

(рис. 1). Знайти розподіл температури всередині ізоляції, а також кількість теплоти, що віддається одним погонним метром труби протягом доби.

Розв’язання. Якщо тіло знаходиться в стаціонарному тепловому стані і температура T в кожній його точці є функцією тільки однієї координати x , згідно з законом теплопровідності Фур’є кількість теплоти, що виділяється за секунду:

86

Звідки закон розподілу температури всередині ізоляції має вигляд:

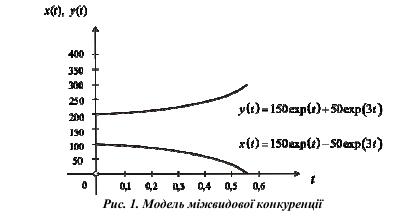
Модель міжвидової конкуренції. Означимо популяцію як будь-яку групу з організмів одного виду, яка обіймає певний простір і є частиною біологічної спільноти – сукупності популяцій, що функціонує як цілісна одиниця у відведеному їй просторі природного середовища.

описує взаємний вплив популяцій двох конкуруючих видів на швидкості їх росту. Припустимо, що початкові популяції нараховують x 0 100 та y 0 200особин. Необхідно встановити чисельності обох видів у довільний наступний часовий період.

Продиференціювавши рівняння (1), отримуємо x t 2x t y t . Але

87

Отже, вимирання першого виду відбувається при 150exp t 50exp 3t 0 , тобто при

exp 2t 3 , звідки t 0.5ln3 0.55 часових одиниць. Після досягнення 0.55 од. часу другий вид

продовжує рости згідно з рівнянням y t 2y t . Його загальним розв'язком є

y t y t0 exp 2 t t0 . При t0 0.5ln 3 і y t0 150exp t0 50exp 3t0 воно відображає ріст популяції другого виду після вимирання першого (рис. 1).

88

МОДЕЛЮВАННЯ СИСТЕМ

ЛЕКЦІЯ 11

СКЛАДАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ

Розглянуто багатоетапний процес складання диференціальних рівнянь для моделювання систем. Приведені приклади задач, які приводять до математичного моделювання систем диференціальними рівняннями, серед яких задачі моделювання процесу охолодження тіла, руху у вʼязкому середовищі, опису вільних коливань. Також розглянуто побудова моделей на основі диференціальних рівнянь в хімії, електродинаміці, ядерній фізиці та теоретичній механіці.

11.1. Поняття про математичному моделюванні

Різноманітні дослідження нашої реальності підтверджують, що вона є занадто складною для того, щоб бути предметом дослідження в науці. Дослідженню доступні лише моделі - умоглядні конструкції, які повинні відбивати істотні властивості реального об'єкта. Заміну вихідного об'єкта його ідеалізованим чином – моделлю – і подальше дослідження цієї моделі називають моделюванням. Якщо модель формулюється в термінах математики, то моделювання називають математичним. Воно поєднує в собі переваги як експериментальних, так і теоретичних методів. Використання моделей дозволяє:

-вивчити явище з подробицями і глибиною, притаманною експериментальним методам;

-відносно швидко досліджувати явище в будь-яких мислимих ситуаціях, в тому числі в таких, які неможливо реалізувати експериментально (коли натурний експеримент довготривалий, дорогий або небезпечний).

Широке поширення моделювання є наслідком високої спільності моделей, які засновані на фундаментальних законах природи – законах збереження маси, енергії, заряду, імпульсу і моменту імпульсу. Спільність виражається в тому, що одні й ті ж моделі описують різні явища. Диференціальний характер законів призводить до того, що більшість математичних моделей записуються у вигляді диференціальних рівнянь або систем таких рівнянь.

Моделювання є багатоетапним циклічним процесом.

Перший і найбільш складний етап пов'язаний з побудовою моделі. Складність цього етапу обумовлено тим, що тут потрібне залучення як засобів аналізу, так і відомостей з конкретної прикладної дисципліни. До моделі пред'являються різні вимоги, з яких найважливішою є вимога адекватності – модель повинна відображати ті характеристики об'єкта, які приймаються як істотні.

На другому, найбільш простому етапі, побудована модель досліджується або точними, або наближеними (зокрема, чисельними) методами. Порівняльна простота другого етапу математичного моделювання обумовлена тим, що завдання дослідження є формальною, виключно математичною. Відомості з прикладної дисципліни тут не використовуються, і для збіжних за формою моделей збігаються і процедури їх аналізу.

Застосування точних аналітичних методів дає рішення в кінцевому вигляді або, у разі операторних методів, як образ деякого інтегрального перетворення (зазвичай - перетворення Фур'є або Лапласа). Використання наближених аналітичних методів дає рішення у вигляді розкладання по функціях від незалежної змінної (як правило - у вигляді статичного ряду або ряду Фур'є). Чисельні методи дозволяють отримати дискретний набір наближених значень шуканої величини.

89

Перевагою аналітичних методів є те, що отримане рішення залишає можливість аналізу впливу істотних ознак на шукану величину (ці ознаки входять у розв’язок як параметри). Однак застосування аналітичних методів виправдано тільки тоді, коли модель порівняно проста і може бути записана у вигляді одного або двох диференціальних рівнянь. На практиці для дослідження зручно застосовувати програмні пакети символьної математики. Такі пакети «самостійно» аналізують характер рівняння і дають рішення в кінцевому вигляді (можливо, що отримане рішення буде містити неелементарні функції). Рудиментарні засоби символьної математики містяться в пакеті Mathcad; для вирішення порівняно складних завдань досить пакету Maple.

У переважній більшості випадків аналітичне розв’язок не може бути отриманий або ж настільки громіздкий, що його аналіз неможливий. У цій ситуації єдина можливість аналізу полягає в застосуванні чисельних методів; при цьому саму процедуру аналізу називають обчислювальним експериментом або імітаційним моделюванням. На практиці в процесі дослідження можна використовувати програмні пакети чисельного аналізу. Як і раніше відзначимо, що обмежені можливості чисельного аналізу представлені в пакеті Mathcad. Розв’язки складних завдань загального характеру часто можна виконати за допомогою пакету MATLAB. Завдання з важливих прикладних областей (задачі моделювання механічних конструкцій, потоків рідини і газу, електричних кіл тощо) розв’язуються за допомогою спеціалізованих пакетів чисельного аналізу. Крім цього, залишається можливість, користуючись загальнодоступним кодом процедур чисельного розв’язування диференціальних рівнянь, розробити авторське програмне забезпечення, призначене для вирішення окремої задачі.

На третьому етапі результати аналізу інтерпретуються в термінах прикладної дисципліни. Тут додатково робляться висновки щодо адекватності моделі. Більше того, часто адекватність перевіряється саме на тестових завданнях - об'єкт штучно поміщається в такі умови, в яких його поведінка відома заздалегідь. Якщо виявляється, що модель призводить до неадекватних результатів, то вона повинна бути змінена (повернення до першого етапу).

11.2. Роль диференціальних рівнянь

Диференціальне рівняння є одним з основних математичних понять. Можна стверджувати, що напевно не знайдеться жодної людини, яка б не чула про них. Диференціальне рівняння – це рівняння для відшукання функцій, похідні яких (або диференціали) задовольняють деяким наперед заданим умовам. Диференціальні рівняння, отримані в результаті досліджень деякого реального явища або процесу, називають диференціальною моделлю цього явища або процесу. Зрозуміло, що диференціальні моделі – це окремий випадок тої множини математичних моделей, які можуть бути побудовані при вивченні оточуючого нас світу. При цьому необхідно відзначити, що існують і різні типи самих диференціальних моделей. В найпростішому випадку моделювання диференціальними рівняннями розглядати лише моделі, які описуються так званими звичайними диференціальними рівняннями. Однією з характерних особливостей цих рівнянь є те, що невідомі функції в них залежать тільки від однієї змінної.

У процесі побудови звичайних диференціальних моделей є важливим, а часом і головним значенням знання законів тої галузі науки, з якою зв’язана природа досліджуваної задачі. Так, наприклад, в механіці це можуть бути закони Ньютона, в теорії електричних кіл - закони Кірхгофа, в теорії швидкостей хімічних реакцій - закон дії мас і т.д.

За звичай, на практиці доводиться мати справу і з такими випадками, коли закони, що дозволяють скласти диференціальне рівняння відомі, і тому необхідно вдаватися до різних припущень та гіпотез, що стосуються протікання процесу за малих змін параметрів – змінних.

Тоді, до диференціального рівняння призводить граничний перехід, і, якщо виявиться, що результати дослідження отриманого рівняння як математичної моделі узгоджуються з дослідними даними, то це і буде означати, що висловлена гіпотеза правильно відображає дійсний стан речей.

На жаль не існує загальної процедури чи алгоритму складання диференціальних рівнянь, оскільки в будь-якому випадку чим глибші знання про фізику та властивості модельованого об’єкту тим більш обґрунтованим і правильним буде побудова його математичної моделі у формі диференціального рівняння.

90