5. Проектирование системы автоматического управления

5.1 Разработка математической модели автоматизированного электропривода

При создании математической модели трехфазного асинхронного электродвигателя целесообразно принять следующие допущения, позволяющие в доступной математической форме выразить соотношения основных параметров и координат электродвигателя:

1. намагничивающие силы обмоток двигателя распределены синусоидально вдоль окружности воздушного зазора;

2. потери в стали статора и ротора отсутствуют;

3. обмотки статора и ротора строго симметричны со сдвигом обмоток на 120 градусов;

4. насыщение магнитной цепи отсутствует.

Уравнения равновесия напряжений для обмоток трех фаз статора имеют вид:

(5.1)

соответственно для трех фаз ротора:

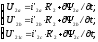(5.2)

где U_1a, U_1b, U_1c, U’_2f, U’_2b, U’_2c – мгновенные значения фазных напряжений статора и ротора;

i_1a, i_1b, i_1c, i’_2f, i’_2b, i’_2c – мгновенные значения фазных токов статора и ротора;

_1a, _1b, _1c, _2a, _2b, _2c – полные потокосцепления фазных обмоток;

R₁, R’₂ – активные сопротивления обмоток статора и ротора;

При математическом описании трехфазных асинхронных электродвигателей удобно оперировать не мгновенными значениями координат, а их результирующими векторами. Если, например, мгновенные значения токов равны i_a, i_b, i_c, то результирующий вектор тока определяется уравнением:

, (5.3)

где .

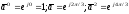Аналогично определяется результирующие векторы напряжения

,

и потокосцепления

.

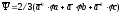Используя выражения результирующих векторов, уравнения (5.1)-(5.2) можно записать в виде одного дифференциального уравнения в векторной форме. Для этого уравнение из (5.1) умножается на 2/3а⁰, второе на 2/3а, третье на 2/3а². Суммируя полученные произведения, получим:

,

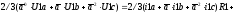
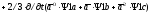или в векторной форме

. (5.4)

Аналогично векторное уравнение напряжений ротора:

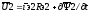. (5.5)

В уравнениях (5.4) и (5.5) векторы записаны соответственно в системах координат статора и ротора. Для совместного решения уравнений их необходимо привести к одной системе координат.

При исследовании переходных процессов в асинхронном электродвигателе, управляемом частотой и напряжением статора, удобно использовать систему координат, вращающуюся со скоростью вращения магнитного поля ₀’, приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю). Предполагается при этом справедливым равенство:

₀’=₁=2f₁,

где f₁ – частота напряжения статора, Гц;

₁ – угловая частота напряжения статора, рад/с.

Для рассматриваемой координатной системы можно записать:

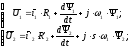(5.6)

где S – скольжение электродвигателя:

,

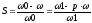(₀=₀’/p – угловая скорость вращения магнитного поля или синхронная скорость электродвигателя).

Потокосцепления связаны с током через индуктивности

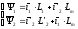(5.7)

Для определения электромагнитного момента двигателя используется векторное произведение ₁i₁, тогда

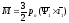, (5.8)

или векторное произведение ₂i’₂, тогда

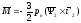. (5.9)

Учитывая (5.7) можно записать (5.8) и (5.9) в виде:

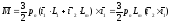, (5.10)

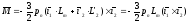(5.11)

Вторые равенства в уравнениях (5.10), (5.11) справедливы потому, что векторное произведение двух одинаково направленных векторов равно нулю.

Для полного описания переходных процессов в асинхронном электродвигателе к уравнениям напряжений добавим уравнение записанное для скалярных значений моментов М и Мс.

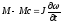, (5.12)

Полученная система уравнений электродвигателя является нелинейной, ее решение для различных динамических режимов возможно с использованием вычислительной техники. Вместе с тем при синтезе систем управления асинхронным электродвигателем целесообразно располагать простыми и наглядными динамическими моделями электродвигателя в виде передаточных функций или структурных схем. Такая возможность появляется, если рассматривать переходные процессы в отклонениях относительно начальных координат электродвигателя. Представим результирующие векторы в виде проекций на комплексной плоскости и запишем их через вещественные и мнимые части в следующем виде:

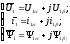
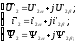(5.13)

Совместив вектор напряжения статора с действительной осью координатной системы, т.е. положив U₁=0. На основании (5.6) получим:

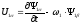, (5.14)

, (5.15)

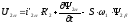, (5.16)

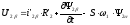. (5.17)

Выразим также электромагнитный момент по уравнения (5.8) через составляющие векторов тока и потокосцепления:

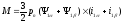
и применив правило векторного произведения векторов, получим абсолютное значение момента

,

;

.

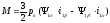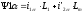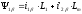Воспользовавшись выражением (5.9), можно аналогично получить:

,

;

.

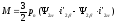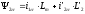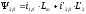Составляющие тока ротора могут быть выражены через составляющие потокосцепления в следующем виде:

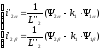, (5.18)

где k₁ – коэффициент электромагнитной связи статора,

, (5.20)

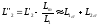, (5.21)

где L₁, L’₂ – полные эквивалентные индуктивности фаз статора и ротора;

L₁, L₂ – индуктивности от полей рассеяния;

L_m – индуктивность главного потока;

L_m=3/2*L₁₂,

где L₁₂ – максимальная взаимная индуктивность между любой обмоткой статора и обмоткой ротора, которая имеет место при соединении их осей.

С учетом (5.7) и (5.19) можно выражения моментов записать в форме, удобной для вывода передаточных функций двигателя:

Или .

В случае одновременного изменения частоты и напряжения статора, при котором потокосцепление статора остается постоянным, из уравнений (5.13) и (5.14) можно получить

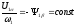; ₁=0. (5.21)

Для двигателя с короткозамкнутым ротом в уравнениях (5.15) и (5.16) U’₂=U’₂=0. Выразив из уравнения (5.18) ₂ и ₂ и подставив их в уравнения (67), (68), получим:

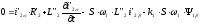, (5.22)

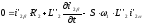, (5.23)

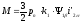. (5.24)

Рассматривая переменные величины в приращениях относительно начальных значений i’₂=I’₂+i’₂, i’₂=I’₂+i’₂, ₁=₁+₁, =+, S=S+S, M=M_нач+M, получим из (5.21)–(5.24) уравнения для астатического режима, связывающие начальные значения координат,

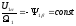, (5.25)

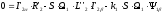, (5.26)

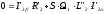, (5.27)

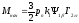, (5.28)

и уравнения для динамического режима, связывающие приращения координат:

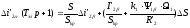, (5.29)

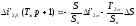, (5.30)

, (5.31)

где Т_эл=L’’₂/R’₂ – электромагнитная постоянная времени электродвигателя;

S_k=R’₂/(L’’₂*₁) – критическое скольжение.

На основании (5.25)-(5.31) можно записать передаточную функцию:

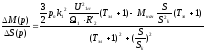. (5.32)

Выражение 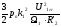в первом слагаемом числителя (5.32) представляет собой значение фиктивного пускового момента М_пф, определяемое в результате линеаризации рабочей части механической характиристики двигателя для принятых значений напряжения статора U₁ и угловой частоты статора ₁:

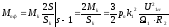, (5.33)

где 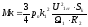–критический момент двигателя.

Момент М_нач во втором слагаемом числителя (84) можно записать с учетом принятых допущений в виде:

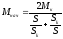. (5.34)

С учетом (5.33) и (5.34) выражение (5.32) примет следующий вид:

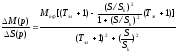. (5.35)

Для рабочей части механической характеристики можно принять (S/S_k)²<<1 и тогда передаточную функцию (5.37) можно записать в упрощенном виде:

.

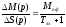Представив зависимость скольжения электродвигателя от угловой частоты напряжения статора в приращениях, и выполнив линеаризацию при условии, что в рабочей области S<<1, получим:

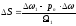. (5.36)

Уравнение равновесия моментов (5.12) может быть записано в приращениях в виде:

. (5.37)

На основании полученных выражений может быть составлена структурная схема асинхронного двигателя при управлении угловой частотой напряжения статора и при условии постоянства потокосцепления статора. Однако это удобнее сделать, если представить базовые значения координат двигателя в о.е., приняв за базовые значения координат их значения в номинальном режиме: М_пфн, _1н., U_1н, _0н=1_н/p_п, где _0н - асинхронная угловая скорость двигателя. Тогда (_он)=, (_11н)=₁, (М/М_пфн)=М, (М_с/М_пфн)=М_с, (U₁/U_1н)=U₁. Передаточная функция (5.35) с учетом (5.36) запишется:

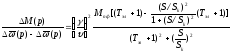, (5.38)

где =U₁/U_1н – относительное напряжение статора;

=₁/_1н – относительная частота напряжения статора.

Или в упрощенном виде:

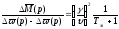. (5.39)

Соответственно на основании уравнения (89) имеем

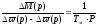, (5.40)

где Т_м=J*_oн/М_пфн – механическая постоянная времени.

Упрощенная структурная схема асинхронного двигателя при управлении угловой частотой напряжения статора, построенная на основании выражений (5.39), (5.40), показана на рисунке 5.1.

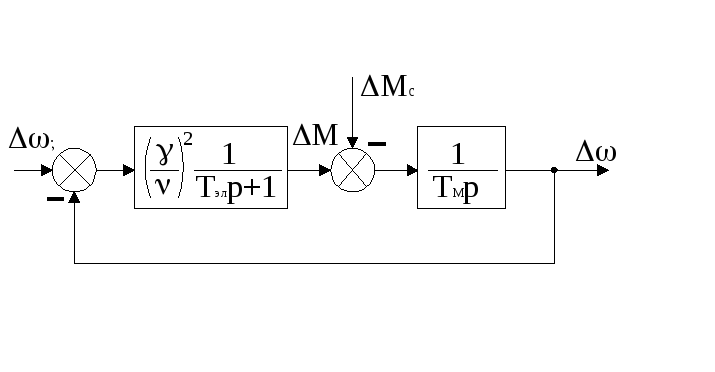
Рисунок 5.1- Структурная схема асинхронного двигателя

_{Момент на валу двигателя, приводящего сушильный барабан во вращение, меняется по закону, изображенному на рисунке 5.2.}

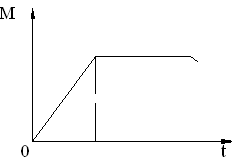
Рисунок 5.2 - Зависимость момента на валу двигателя сушильного барабана от времени

_{T – время достижения моментом установившегося значения.}

_{Время Т обусловлено скоростью заполнения сушильного барабана каменными материалами.}

Закон изменения момента можно описать следующей зависимостью:

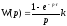, (5.41)

где =Т/3 – постоянная времени данного динамического звена;

k=М/ – коэффициент, определяющий зависимость момента от скорости.

Температура каменных материалов при прохождении через сушильный барабан меняется по следующему закону, изображенному на рисунке 5.3.

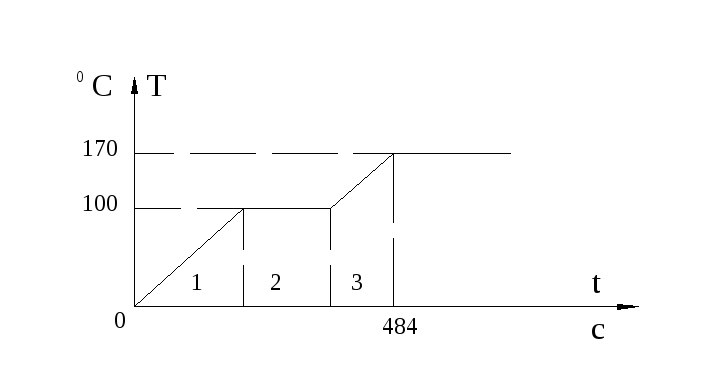
Рисунок 5.3 - Закон изменения температуры каменных материалов

Интервал 1 обусловлен тем, что происходит нагрев каменного материала от температуры окружающей среды до температура 100⁰С.

На интервале 2 происходит испарение влаги, находящейся в материале.

На интервале 3 происходит нагрев каменных материалов от температуры 100С до заданной (в подавляющем большинстве случаев до температуры 170С).

Таким образом, мы можем получить информацию о температуре материала спустя 484 секунды с момента его поступления в сушильный барабан. Такой процесс можно описать звеном с передаточной функцией:

.
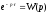