2 Практические занятия

2.1 Расчетная часть

Функциональная схема исследуемой системы стабилизации скорости вращения электродвигателя постоянного тока с независимым возбуждением (ДПТ с НВ) показана на рисунке 2.1.

В системах электропривода из многих координат (напряжение преобразователя, ток двигателя, его момент, скорость, скорость или перемещение рабочего органа) обычно одна является основной регулируемой координатой, по которой осуществляется главная обратная связь. При использовании тиристорных или других быстродействующих преобразователей структура силовой части электропривода оказывается достаточно простой, что позволяет легко осуществить коррекцию контура. При этом оказывается возможным ограничить пределы изменений одной или нескольких промежуточных координат (например, тока двигателя, скорость при отработке перемещений и т. п.). С этой целью система дополняется дополнительными обратными связями по указанным координатам.

Рассматриваемая далее система является двухконтурной и построена она по принципу подчиненного регулирования, который поясняется рисунком 2.1. Здесь предусмотрены два контура регулирования: скорости и тока со своими регуляторами РС и РТ, причем выходное напряжение регулятора внешнего контура скорости U_рс является предписанным для внутреннего контура тока. Выходное напряжение регулятора тока U_РТ является управляющим для тиристорного преобразователя ТП. Регуляторы предназначены для коррекции динамических свойств контуров регулирования.

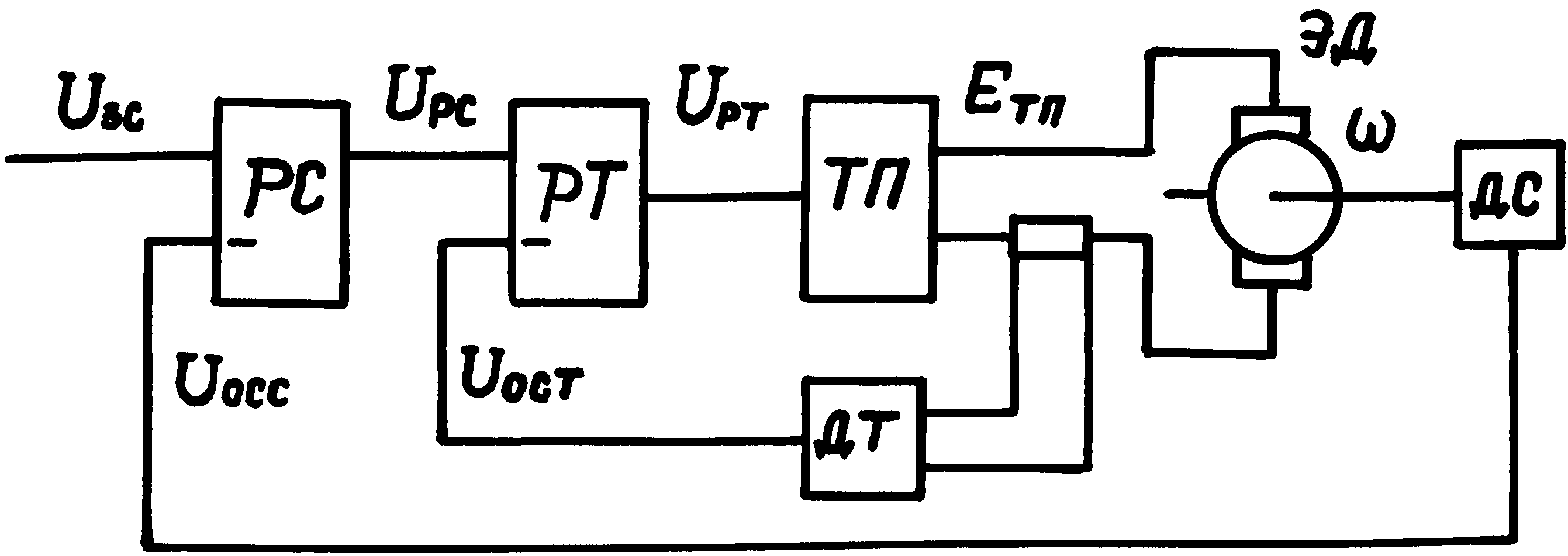
Рисунок 2.1 Функциональная схема двухконтурной системы ЭП

На рисунке 2.1 приняты следующие обозначения элементов системы ЭП:

• РС - регулятор скорости;

• РТ - регулятор тока;

• ТП - тиристорный преобразователь;

• ДТ и ДС - датчики тока и скорости соответственно;

• ЭД – электродвигатель.

Сигналы в функциональной схеме:

• U_зс - напряжение задания скорости;

• U_occ - напряжение отрицательной обратной связи по скорости;

• U_рс - напряжение на выходе регулятора скорости;

• U_ocт - напряжение отрицательной обратной связи по току;

• U_рт=U_упр - напряжение на выходе регулятора тока;

• E_тп - ЭДС на выходе тиристорного преобразователя;

•  - угловая скорость вращения электродвигателя ЭД.

2.2 Математическое описание элементов системы эп

2.2.1 Математическое описание электродвигателя

При математическом описании двигателя постоянного тока с независимым возбуждением принимаются следующие допущения:

а) размагничивающее действие реакции якоря скомпенсировано;

б) параметры двигателя считаются неизменными;

в) механические потери и потери в стали двигателя не учитываются;

г) магнитный поток считается постоянным.

Линеаризованная математическая модель двигателя постоянного тока с независимым возбуждением описывается системой дифференциальных уравнений в операторной форме:

E_тп(p)-E(p)=R_яцI_я(p)+L_яцpI_я(p);

E(p)=C(p);

M_эм(p)=CI_я(p);

M_эм(р)-М_с(р)=J_прp(p),

где E_тп(p) - изображение ЭДС тиристорного преобразователя;

E(p) - изображение противо-ЭДС электродвигателя;

I_я(p) - изображение тока якоря;

(p) - изображение скорости электродвигателя;

M_эм(p) - изображение момента электродвигателя,

М_с(р) - изображение момента сил статических сопротивлений;

R_яц - суммарное сопротивление якорной цепи;

L_яц - суммарная индуктивность якорной цепи;

J_пр - суммарный момент инерции ЭП, приведенный к валу двигателя;

С - конструктивный коэффициент электродвигателя.

Указанным уравнениям соответствуют динамические звенья, описываемые передаточными функциями:

а) якорная цепь электродвигателя

W_яц(р)= = = = ;

где T_яц – суммарная постоянная времени цепи якоря.

б)электромагнитная часть двигателя

W_эмч(р)==С;

в)механическая часть электродвигателя

W_мч(р)==;

г)внутренняя обратная связь по ЭДС двигателя

W_эдс(р)==C.

На основе системы уравнений электродвигатель постоянного тока с независимым возбуждением можно представить следующей структурной схемой.

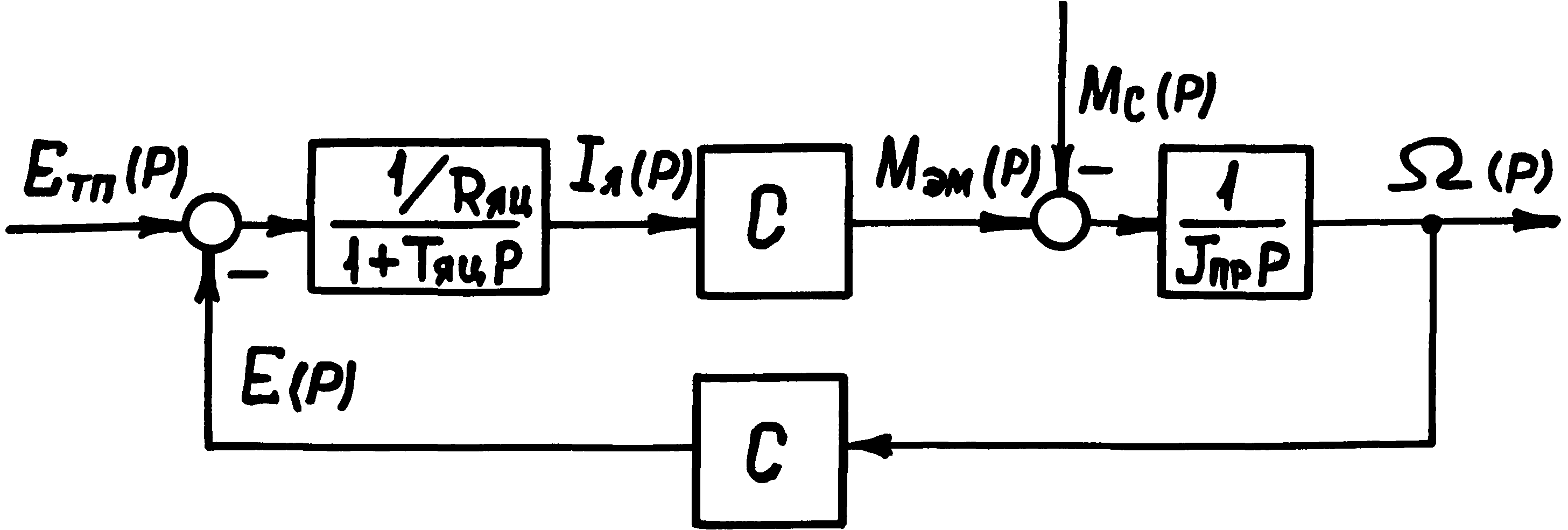
Рисунок 2.2 - Структурная схема ДПТ С НВ