Задание

1 АНАЛИЗ ЛИНЕЙНОЙ СУ

По заданной структурной схеме системы управления (СУ) построить АФЧХ разомкнутой и замкнутой системы. Исследовать устойчивость СУ по одному из критериев. Определить запасы устойчивости по фазе и амплитуде. Построить переходный процесс в системе. По переходному процессу провести анализ качества управления и определить все его показатели. При неудовлетворительном качестве управления дать рекомендации по его улучшению.

x(p)

y(p)

W₁(p)

W₅(p)

W₂(p)

W₃(p)

W₄(p)

W₆(p)

W₇(p)

Схема 1.1

2 Анализ нелинейной су

x(p)

y(p)

W₁(p)

W₅(p)

W₂(p)

W₃(p)

W₄(p)

W₆(p)

W₇(p)

НЭ

Схема 2.1.

Нелинейный элемент:

7

-5

5

-7

1 Анализ линейной су

1. Упрощение структурной схемы СУ

Избавимся от последовательного соединения звеньев W₂(p), W₃(p), W₄(p):

x(p)

y(p)

W₁(p)

W₅(p)

W₂₃₄(p)

W₆(p)

W₇(p)

Схема 1.2.

Передаточные функции этой системы имеют вид:

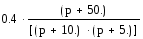
W234(p)=

Далее избавимся от внутреннего встречно-параллельного участка схемы:

x(p)

y(p)

W₁(p)

W₅(p)

W₂₃₄₆(p)

W₇(p)

Схема 1.3.

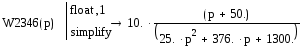
Теперь имеем:

x(p)

y(p)

Wпр(p)

Wос(p)

Схема 1.4.

Передаточная функция прямого участка цепи:

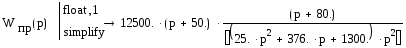
Передаточная функция цепи обратной связи:

В итоге имеем:

Передаточная функция замкнутой системы:

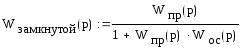
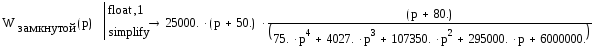
Передаточная функция разомкнутой системы:

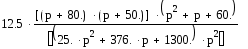
W_раз =

1.2 Построение афчх системы

Перейдем от операторной формы записи передаточных функций к передаточным функциям, записанных в изображениях по Лапласу.

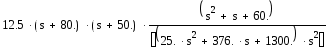
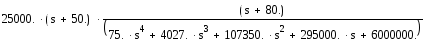
Получим частотную форму записи передаточных функций.

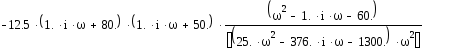
Выделим действительную и мнимую части:

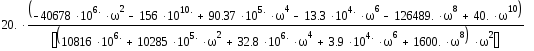
W_раз(i)= +

+

= –

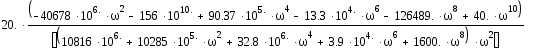
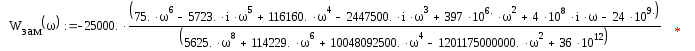
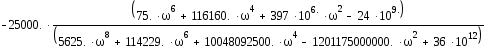
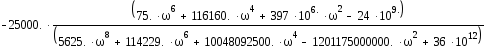
Построим АФЧХ замкнутой СУ:

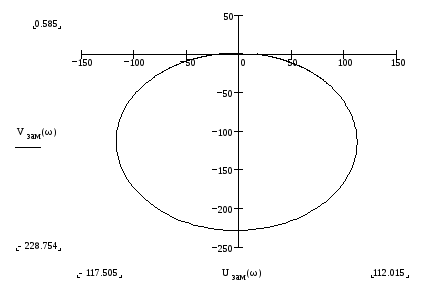
График 1.2.1.

Для построения графика 1.2.1 использовались дискретные значения:

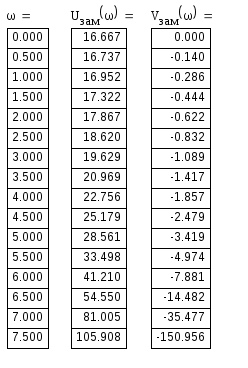
1. Построение АЧХ, ЛАЧХ и ФЧХ системы

1.3 Построение АЧХ, ЛАЧХ и ФЧХ системы

1.3.1 АЧХ замкнутой системы

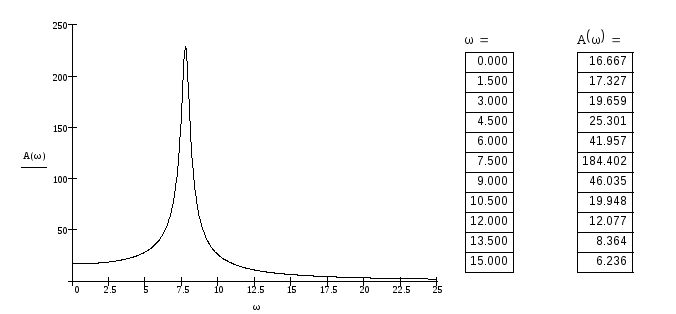График 1.3.1.

1.3.2. ФЧХ

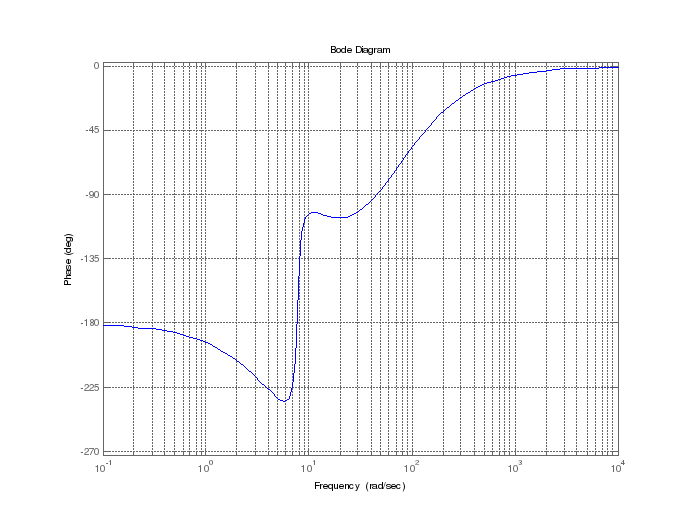
График 1.3.2.

1.3.3. ЛАЧХ

График 1.3.3.

4. Исследование устойчивости СУ

Проверим систему на устойчивость, по критерию устойчивости Ляпунова.

Устойчивость по Ляпунову означает, что все корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости.

Найдем корни характеристического уравнения для замкнутой системы:

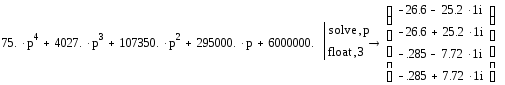
Так как все вещественные части корней отрицательны, то корни характеристического уравнения находятся в левой полуплоскости комплексной плоскости, а это означает устойчивость системы.

1.5 Определение запасов устойчивости

П остроим ЛАЧХ, ЛФЧХ для разомкнутой системы (см. график 1.5.)

Г

h



рафик 1.5

6. Переходный процесс

t_н

t_p

T

h₂

h_max

t_max

h_ycm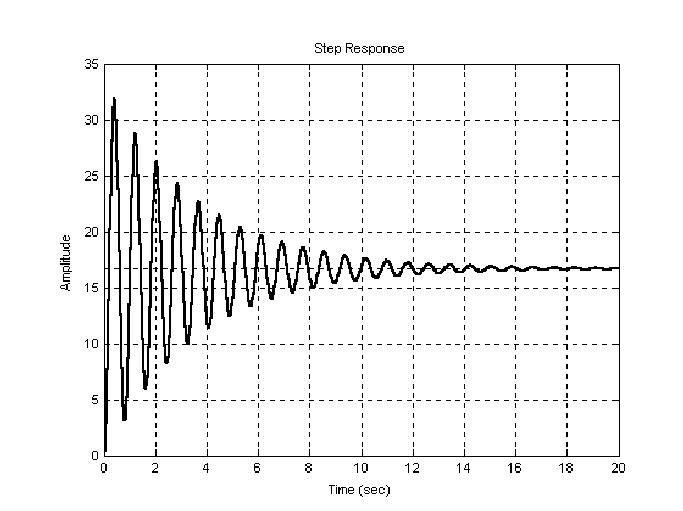

График 1.6.