1.3 Определение требуемого коэффициента усиления разомкнутой сау из условия статической точности

Исходный коэффициент разомкнутой системы равен: .

Найдем требуемый коэффициент усиления разомкнутой системы. Исходя из анализа полученной передаточной функции разомкнутой системы, можно утверждать, что система астатична.

Тогда требуемый коэффициент усиления разомкнутой системы найдем по формуле:

где ,. Следовательно .

Коэффициент передачи дополнительного усилителя выразим из формулы:

Дополнительный усилитель можно поставить в главный контур САУ в начале:

Рисунок 3 – Структурная схема САУ с k_пу

1.4 Определение передаточных функций замкнутой сау по управляющему, возмущающему воздействию и по ошибке

Разделим нашу САУ на две части: до возмущающего воздействия, и после –.

Рисунок 4 – Упрощенная структурная схема САУ

Уравнение системы в операторной форме:

,

,

Передаточная функция замкнутой САУ по управляющему воздействию:

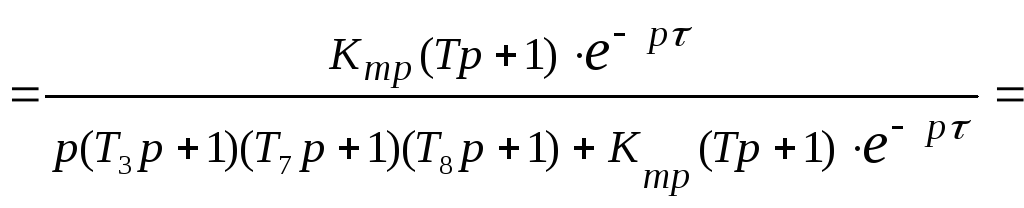
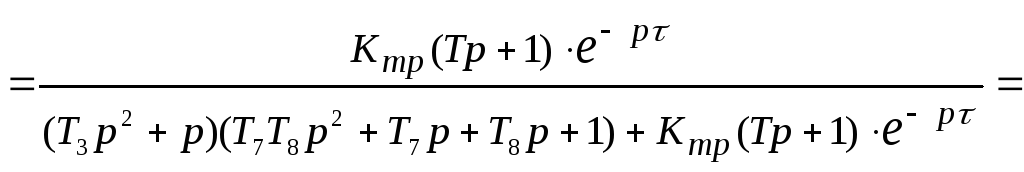
Передаточная функция замкнутой САУ по возмущающему воздействию:

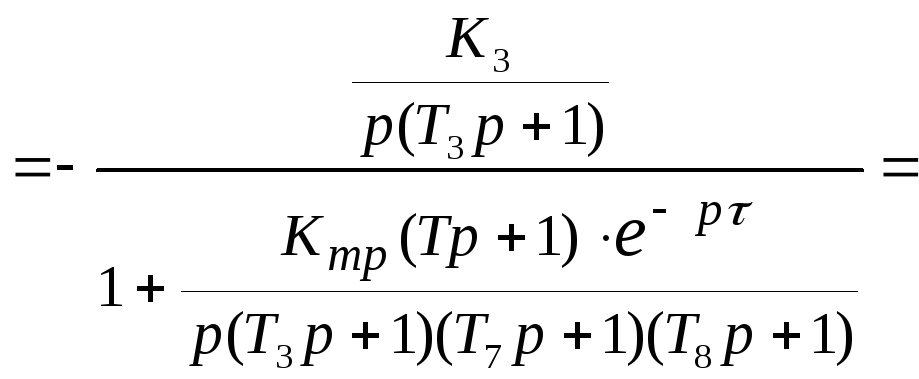
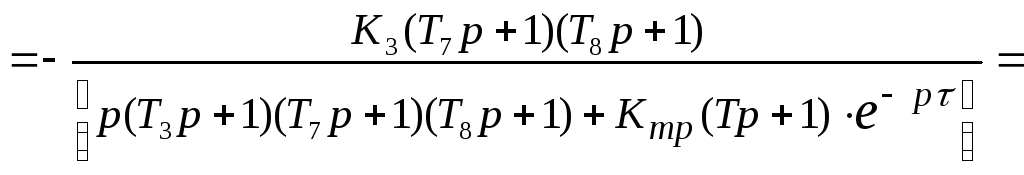
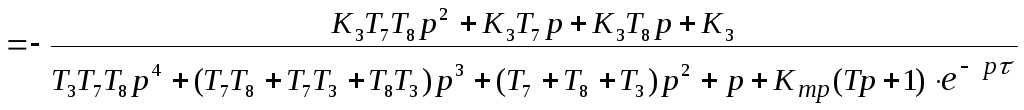
Ошибка определяется как разность входной и выходной координаты:

Передаточная функция замкнутой САУ по ошибке управляющего воздействия:

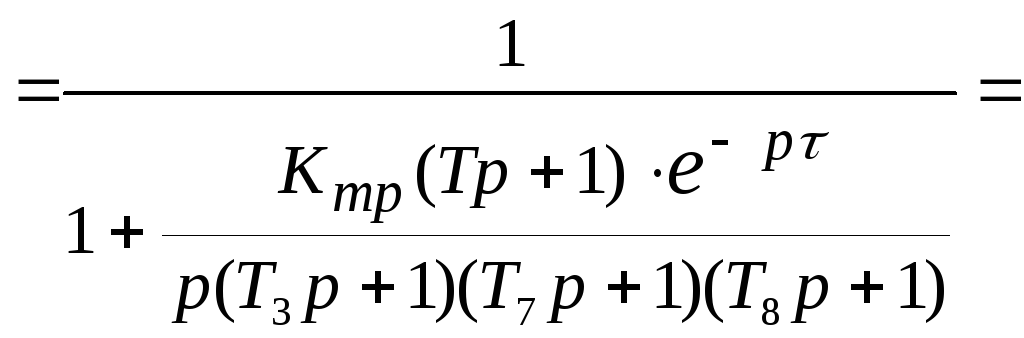
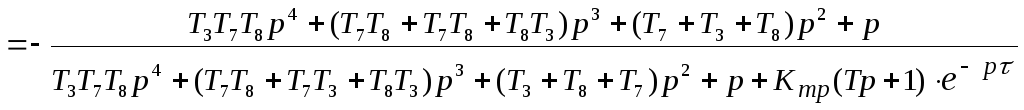
Передаточная функция замкнутой САУ по ошибке возмущающего воздействия:

1.5 Выводы по проведенному анализу

Исходная САУ состоит из пяти динамических звеньев: трех инерционных ,,, интегрирующего звенаи звена запаздывания.Первый контур представляет собой соединенные и. Второй контур – это последовательно соединенные первый контур, звенья , и интегратор , охваченные единичной отрицательной обратной связью.

Так как в главном конуре САУ есть один интегратор, то разомкнутая САУ имеет астатизм первого порядка.

Изначально разомкнутая САУ имеет коэффициент усиления . Чтобы обеспечить необходимую точность, нужен коэффициент. Для этого в начало главного контура включаем промежуточный усилитель..

2. Анализ устойчивости сау

2.1 Анализ устойчивости замкнутой сау с помощью алгебраического критерия Раусса.

Характеристическое уравнение замкнутой системы имеет вид:

Здесь

Коэффициенты положительны, следовательно, необходимое условие устойчивости выполняется. Проанализируем характеристическое уравнение, используя достаточное условие, то есть, используем критерий Раусса.

Таблица Раусса составляется следующим образом:

Формулировка критерия Раусса:

САУ устойчива, если положительны все коэффициенты первого столбца таблицы Раусса.

Так как ,следовательно, достаточное условие не выполняется. САУ неустойчива.

Определим значение , при котором САУ будет устойчива по критерию Раусса. Итак, чтобы САУ была устойчива, необходимо, чтобы.

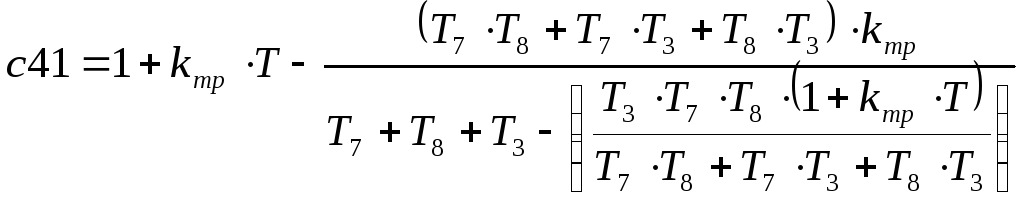
Решив это уравнение относительно , получаем:

, т.е. САУ устойчива, при .

2.2 Анализ устойчивости с использованием критерия Найквиста

Данный метод позволяет судить об устойчивость замкнутой САУ по АФХ разомкнутой системы.

Характеристическое уравнение системы разомкнутого типа имеет вид:

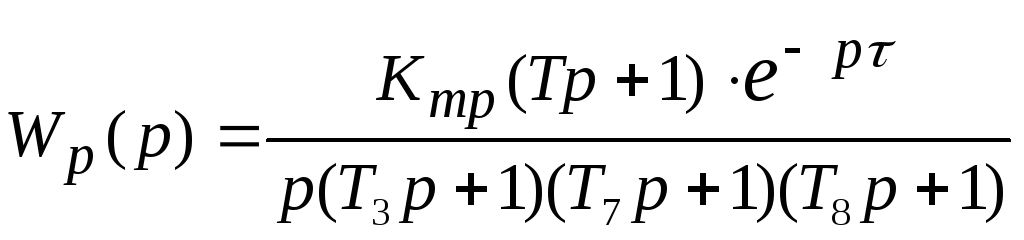
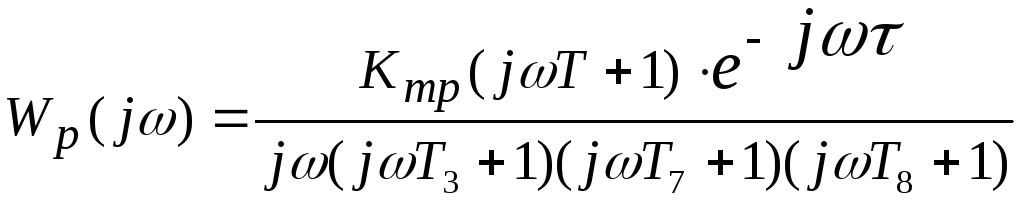
Представим выражение в виде суммы вещественной и мнимой частей:

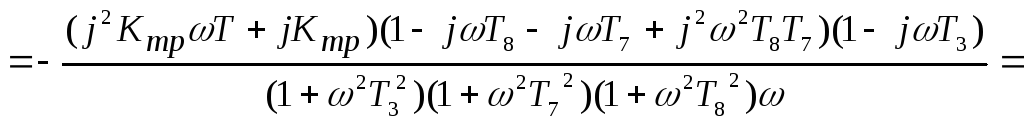
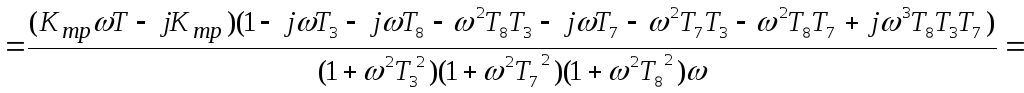
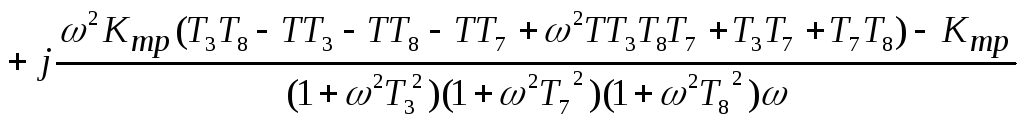
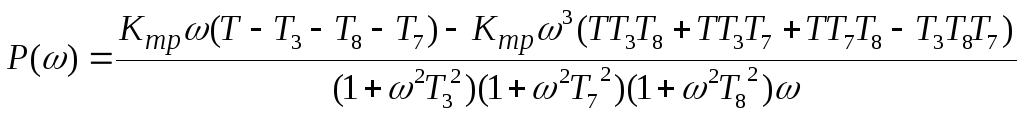
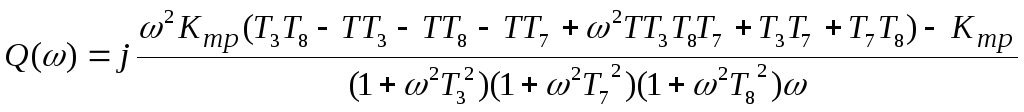
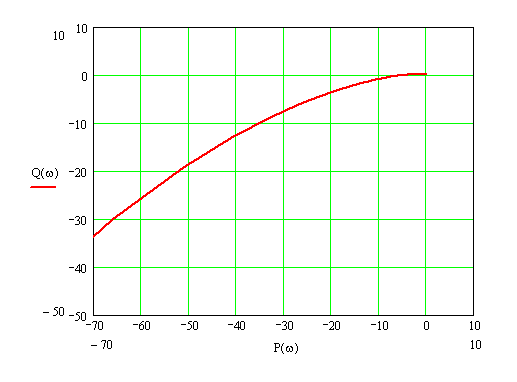
Рисунок 5 – АФХ разомкнутой САУ

Найдём точку пересечения АФХ с вещественной осью, для этого приравняем мнимую часть к 0 и решим относительно :

Подставим найденное значение в вещественную часть:

Увеличим масштаб рисунка 5, чтобы посмотреть нужную область:

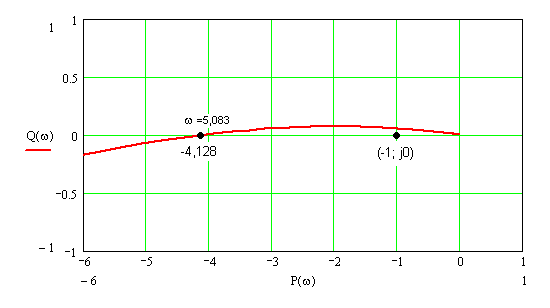
Так как АФХ данной разомкнутой системы охватывает критическую точку (-1;j0), то на основании критерия Найквиста замкнутая система является неустойчивой.