Типа не и и-не.

1.5. Порядок выполнения лабораторной работы №1.

Цели работы: изучить способы формального описания работы логических элементов, формулы преобразования переключательных функций, методы исследований и способы их отображения с применением технических средств проектирования.

Для этого:

• нарисовать в редакторе Word или в каком либо графическом редакторе принципиальную схему реализации минимальной переключательной функции трех аргументов, заданную шестнадцатеричным числом по указанию преподавателя,

• исследовать в среде графического моделирования LabVIEW законы функционирования схем, реализующих функционально полные наборы (И, ИЛИ, НЕ), (И – НЕ), (ИЛИ – НЕ),

• исследовать в среде графического моделирования LabVIEW работу схемы минимальной логической функции трех аргументов, заданной шестнадцатеричным числом.

Отчёт о проделанной работе. Составляя отчёт нужно исходить из принципа, что научное описание работы должно быть таким, чтобы её мог повторно проделать другой человек такой же квалификации. Поэтому он должен включать все алгебраические преобразования переключательных функций и схемы всех экспериментов.

Решение.

Шестнадцатеричное число 0хА5 в двоичной форме выражается числом 10100101. Это и есть значение переключательной функции на независимых наборах переменных, начиная с нулевого набора. Запишем переключательную функцию в табличной форме (таблица 1.6).

Таблица 1.6

A	0	0	0	0	1	1	1	1
B	0	0	1	1	0	0	1	1
C	0	1	0	1	0	1	0	1
F(ABC)	1	0	1	0	0	1	0	1

Теперь представим функцию в совершенной дизъюнктивной нормальной форме.

Построим диаграмму Вейча и найдём минимальную форму (табл.1.7) . Таблица 1.7

		1	1
	1			1

. Нарисуем реализацию этого выражения на элементах, обозначенных по российскому ГОСТу.

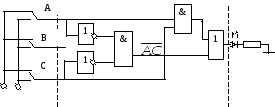
Лог 1 Лог 0

Control Palette Function Palette Indication

Рис.1.5. Реализация функции, заданной таблицей 1.6

Лабораторная работа №2. Логические элементы средней степени интеграции.

Шифратор. Шифратором называется схема, у которой подача сигнала на один из входов приводит к появлению на выходах определённой кодовой комбинации. Подача сигналов на 2 и более входов запрещена. Его условное обозначение и таблица истинности представлены на рис. 1.6.

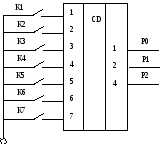
Таблица истинности

	P2	P1	P0
K1	0	0	1
K2	0	1	0
K3	0	1	1
K4	1	0	0
K5	1	0	1
K6	1	1	0
K7	1	1	1

ЛОГ 1

Рис.1.6. Схема шифратора.

Переключательные функции, описывающие схему шифратора, могут быть получены следующим образом. В строках К1 – К7 таблицы истинности запишем двоичные числа, соответствующие номеру ключа. Переключательные функции Р0, Р1, Р2 должны быть равны 1 при замыкании любого из ключей равных 1 в соответствующем столбце, то есть должны решать логическую функцию ИЛИ и имеют следующий вид:

P0 = K1 v K3 v K5 v K7; P1 = K2 v K3 v K6 v K7; P2 = K4 v K5 v K6 v K7

С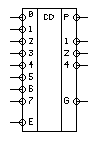овременный шифратор ИВ1 (рис. 1.7) выполнен в виде интегральной схемы малой степени интеграции и имеет некоторые дополнительные выводы, позволяющие объединять два и более шифраторов для получения большего числа входов. Эта микросхема имеет восемь информационных входов 0 – 7 и вход разрешения Е. Выходы 1, 2, 4 – инверсия выходного кода, G – признак подачи входного сигнала и Р – признак переноса. Если на входе Е – 0, а на всех информационных входах 1, то на выходах 1, 2, 4, G – 1, а на выходе Р – 0. При подаче 0 на любой из информационных входов на выходах 1, 2, 4 появляется соответствующая инверсная кодовая комбинация, на выходеG – 0, что является признаком подачи входного сигнала, а на выходе P – 1, которая запрещает работу другого шифратора при каскадном соединении. При Е = 1 на всех выходах микросхемы – 1.

Рис. 1.7. Микросхема 155 ИВ1