2.3.3 Генерирование случайных воздействий

В процессе имитации функционирования сложных систем приходится моделировать различные случайные воздействия, которым всегда подвергается система в реальных условиях. Кроме того, процесс функционирования любой системы также носит случайный характер, и его имитация требует выработки большего числа случайных чисел. Алгоритмы формирования последовательностей случайных чисел, распределенных по некоторому закону, предполагают наличие базовой последовательности случайных чисел. В качестве такой принята последовательность случайных чисел, равномерно распределенных в интервале (0,1). Действуя на эту последовательность специально подобранными функциями, можно получить случайную величину с любым заданным законом распределения.

Как известно, плотность вероятности равномерно распределенной в интервале (0,1) случайной величины имеет следующий вид:

а функция распределения

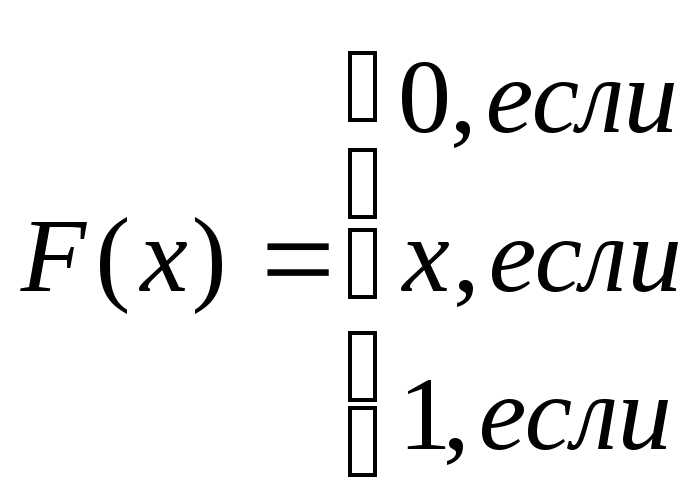
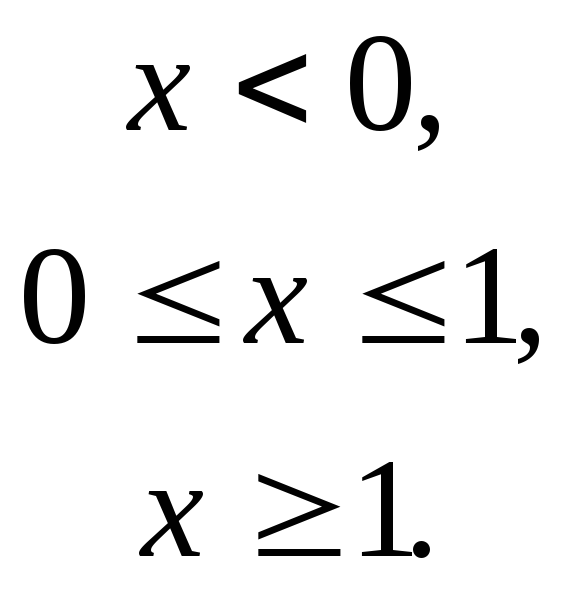
При этом математическое ожидание и дисперсия равны соответственно:

M[X]=1/2 , D[X]=1/12.

Идея формирования равномерно распределенной случайной величины заключается в следующем.

Пусть дискретная случайная величина Z_i принимает только два значения 0 и 1 с равными вероятностями, т.е.

P(Z_i =0)=P(Z_i =1)=1/2.

Рассмотрим бесконечную последовательность Z₁ ,..., Z_n ,...таких величин, независимых между собой, и будем считать их двоичными знаками некоторого числа X, равного

Очевидно, что все значения X лежат в пределах 0x1.

При этом

_{. . . . . . . . . . . . . . . . . . . . . . . . . . .}

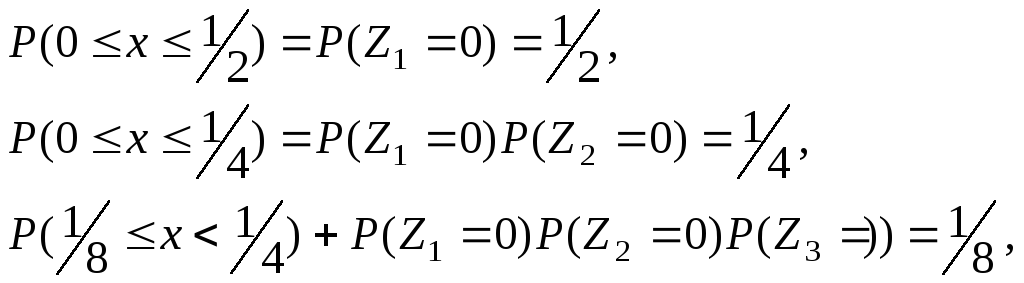
Следовательно, величина X равномерно распределена в (0,1). Таким образом, для формирования значений случайной величины, равномерно распределенной в (0,1), нужно сформировать бесконечную последовательность случайных чисел, с равной вероятностью принимающих значения 0 и 1, и считать их двоичными знаками дроби X, являющейся искомым значением.

В ЭВМ, где для записи числа предусмотрено не более k разрядов, нельзя записать бесконечную двоичную дробь. Поэтому каждое число X, представляемое в виде k- последовательности из 0 и 1, нельзя считать значением равномерно распределенной случайной величины. Это распределение называется квазиравномерным. Чем оно больше, тем точнее приближает равномерное распределение.

Существует два способа формирования случайных чисел на ЭВМ. Первый способ предполагает их выработку с помощью специальных электронных приставок, датчиков, связанных с ЭВМ. Вторым способом является генерирование чисел самой машиной специальным алгоритмом.

Программное генерирование случайных чисел. Известно множество методов машинной имитации равномерно распределенной случайной величины. Соответствующие программы-генераторы вычисляют так называемые псевдослучайные числа, которые, не являясь случайными, обладают статистическими свойствами случайных чисел, равномерно распределенных в интервале (0,1).

Последовательность чисел, полученная с помощью идеального генератора, должна состоять: 1) из равномерно распределенных, 2) статистически независимых, 3) воспроизводимых, 4) неповторяющихся чисел. Кроме того, идеальный генератор должен работать быстро и занимать минимальный объем машинной памяти.

Большинство алгоритмов, используемых на практике для получения псевдослучайных чисел, представляет собой рекуррентные формулы первого порядка:

(2.3)

где начальное число X₀ задано. Рекуррентный характер алгоритмов генерирования случайных чисел порождает при их реализации на ЭВМ периодические последовательности. Так как код любой ЭВМ содержит всегда конечное число разрядов, то в этом коде можно записать лишь конечное число N чисел, заключенных между 0 и 1. Поэтому рано или поздно некоторое значение X_L совпадает с получением X_R . Тогда исходя из формулы (2.3),

X_R+i = X_L+i (i=1,2,...). (2.4)

Если L – наименьшее число, удовлетворяющее условию (2.4) при некотором R (R<L), то множество чисел X₀ ,X₁ ,...,X_L-1 называется отрезком апериодичности, L - длиной отрезка апериодичности, а P=L-R – периодом последовательности.

Так как одним из условий идеального генератора является неповторяемость чисел, то необходимо знать значения L и P для каждой последовательности и использовать для расчетов не более L чисел из нее.

Конгруэнтные методы генерирования случайных чисел. В настоящее время широкое распространение получили конгруэнтные методы генерирования псевдослучайных чисел, которые используют фундаментальное соотношение конгруэнтности, выражаемое следующей формулой:

(2.5)

где X_i –i-ый элемент последовательности; , , m - неотрицательные целые числа. Выражение означает, что z есть остаток от деления y на m. Два целых числа X_i+1 и X_i конгруэнтны по модулю m (m – целое) тогда и только тогда, когда существует такое целое к, что X_i+1- X_i = , т.е., если разность X_i+1- X_i делится на m и если числа X_i+1 и X_i дают одинаковые остатки от деления на m.

Если задано начальное значение X₀ , множитель  и аддитивная константа , то по формуле (2.5) можно определить последовательность целых чисел { X₁ ,X₂ ,...,X_i ... }, равномерно распределенных в интервале (0,m). Поделив все числа на m, легко получить последовательность псевдослучайных чисел с равномерным в (0,1) распределением.

Существуют различные конгруэнтные преобразования, которые можно разделить на три группы: 1) мультипликативные, 2) аддитивные, 3) смешанные. Каждый тип преобразования определяет способ генерирования псевдослучайных чисел.

Мультипликативный метод.

Мультипликативный конгруэнтный алгоритм задает последовательность неотрицательных целых чисел { X_i }, не превосходящих m, по формуле

(2.6)

представляющей собой частный случай формулы (2.5) при =0. Последовательность, полученная по этому методу, обладает достаточно хорошими статистическими характеристиками. Выбирая параметры  и X₀, с его помощью можно получить последовательность равномерно распределенных некоррелированных псевдослучайных чисел. Более того, при выполнении определенных условий, накладываемых на эти параметры, генерируемая мультипликативная последовательность обладает максимальным при данном модуле m периодом.

Мультипликативный алгоритм требует минимального объема машинной памяти, и с вычислительной точки зрения сводится к подсчету произведения двух целых чисел - операции, которая очень быстро выполняется современными ЭВМ.

Для численной реализации наиболее удобна версия алгоритма, в которой модуль m равен , где p - основание системы счисления, используемой в ЭВМ, а l - длина машинного слова.

Выбор m=p^l удобен по двум причинам. Во-первых, вычисление остатка от деления на m сводится к выделению l младших разрядов делимого. Во-вторых, преобразование целого числа X_i в рациональную дробь из интервала (0,1) осуществляется подстановкой слева от него двоичной или десятичной запятой. Таким образом, специальный выбор числа m позволяет исключить из процесса счета две операции деления.

Для ЭВМ с p=2 (внутренний алфавит – двоичный) формулу (2.6) удобнее представить в следующем виде:

где d – число десятичных цифр в машинном слове. Алгоритм построения последовательности будет иметь вид:

1. Выбрать в качестве X₀ любое нечетное.

2. Вычислить по формуле

_,

где t - любое целое положительное число.

3. Вычислить произведение X₀ содержащее не более 2d значащих разрядов.

4. Взять d младших разрядов полученного числа в качестве X₁ , остальные отбросить.

5. Поставить десятичную запятую слева от найденного числа X_i . Полученную дробь считать за X_i , то есть

6. Принять X₀= X₁.

7. Вернуться к п.3.

Пример.

Пусть d=4. Мультипликативный генератор определит в этом случае p=5*2^4-2=200 различных чисел.

1. Возьмем n₀ =5379.

2. Для t=0 и z=91 можно взять =91. Пусть =91.

3. n₀ =91*5379=00489489. Отсюда n₁ =9489, x₁ =0,9489.

4. n₁ =91*9489=00863499. Отсюда n₂ =3499, x₂ =0,3499.

5. n₂ =91*3499=00318409. Отсюда n₃ =8409, x₃ =0,8409 и тек далее.

(n₄ =5219,n₅ =4929,n₆ =8539,...).

Из примера видно, что младшие разряды полученных чисел не напоминают случайные. Мультипликативная процедура обеспечивает полный период высшему разряду генерируемых значений, и с понижением порядка период уменьшается. Таким образом, если эксперимент позволяет ограничиться выборкой, состоящей из чисел, включающих меньше значащих цифр, чем укладывается в машинное слово, надо использовать высшие порядки чисел мультипликативного генератора.

Аддитивный метод.

Аддитивный конгруэнтный алгоритм базируется на следующей формуле:

_{Xi=( Xi-1+ Xi-k)(modm)}

Аддитивные методы используются редко, и характеристики получаемых последовательностей изучены слабо. Модуль m выбирается так же, как и в мультипликативных методах. Период последовательности, получаемый аддитивным алгоритмом, равен , где p_k - постоянная величина, зависящая от k и p. Например, при l=35, p=2, p_k =255, k=16 период равен 255*2³⁴ .

Смешанный метод

Смешанная конгруэнтная процедура вычисляет последовательность неотрицательных целых чисел {X_i}, не превосходящих заданную величину m, по формуле (2.5).

В отличие от мультипликативного метода здесь 0. Преимущество смешанной процедуры в том, что при данном m можно подобрать параметры  и , для которых по формуле (2.5) получается последовательность чисел, с малой степенью корреляции. С вычислительной точки зрения смешанный метод сложнее мультипликативного на одну дополнительную операцию сложения.

Комбинационный метод

Конгруэнтные методы не всегда дают статистически удовлетворительные последовательности. Элементы получаемых последовательностей часто являлись статистически зависимы. Поэтому возникли новые разновидности конгруэнтных алгоритмов, названы комбинационными методами, объединяющими два или более конгруэнтных алгоритма.

Комбинация алгоритмов может быть проведена, например, следующим образом. С помощью мультипликативного алгоритма вычисляется последовательность из p чисел. Затем с помощью смешанного алгоритма формируется целое число i из интервала (0,p). Из набора псевдослучайных чисел извлекается число с номером i, и процедура повторяется дальше. Этот комбинационный метод успешно выдержал все проверки, но он является сравнительно сложным, и из двух генерируемых последовательностей в конечном счете используется только одна.

На практике обычно используется мультипликативный конгруэнтный алгоритм, параметры которого выбираются в соответствии с рядом дополнительных условий, уменьшающих автокорреляцию чисел.

2.3.4 Проверка качества генерируемых последовательностей

Качество генерируемых последовательностей определяется их статистическими свойствами, а именно случайностью получаемых чисел, их равномерной распределенностью в интервале (0,1) и независимостью. Поэтому все последовательности псевдослучайных чисел, полученные с программ-генераторов, должны быть проверены с помощью специальных тестов на случайность, равномерность и некоррелированность. В основе многих тестов проверки качества получаемых последовательностей лежит критерий ² Пирсона, позволяющий проверить соответствие эмпирического распределения случайной величины X и предполагаемого теоретического. Схема применения критерия следующая. Выборка объема n из значений случайной величины X разбивается на  интервалов одинаковой длительности. Затем определяются значения n_i - количество попаданий величины X в i-ый из разрядов. С помощью таблиц вычисляется значение p_i теоретической вероятности попадания случайной величины в i-ый интервал. Далее подсчитывается наблюдаемое значение критерия по формуле:

,

Известно, что случайная величина ² распределена по закону ² с числом степеней свободы k, где  - число разрядов выборки, а k -число неизвестных параметров предполагаемого распределения. Критическая область для критерия – правосторонняя. Критическая точка ²_кр определяется из таблиц ² - распределения по уровню значимости  и числу степеней свободы исходя из условия

P(² >²_кр )=.

Если >²_кр , то гипотеза о соответствии распределений отвергается. Если <²_кр , то она не противоречит опытным данным.

Проверка случайности. Для того, чтобы проверить, насколько хорошо генерируемая последовательность имитирует последовательность случайных чисел, наиболее часто используется тест серий. С его помощью проверяется один из разрядов (обычно старший) чисел полученной последовательности. При более тщательной проверке исследуются независимо друг от друга несколько старших разрядов.

Пусть получена последовательность x₁ ,..., x_n псевдослучайных чисел из интервала (0,1). Обозначим символами ₁ ,..., _n цифры старшего разряда чисел последовательности. Цифры _k+1,...,_k+ образуют серию длины , если _k+1 =_k+2 =...= _k+._k++1 . Количество серий длины  во всей последовательности обозначим K_ (=1,n), а общее число серий

.

Известно, что длина  последовательности подчинена биномиальному закону. Для того, чтобы установить случайность последовательности, нужно проверить гипотезу о законе распределения с помощью одного из критериев (тестов) согласия, например ².

Критерий ² в данном случае имеет следующий вид:

.

При этом

p_=P(_k+1 =_k+2 =...= _k+._k++1)=9*10^- .

Так как, начиная с некоторой длины m серии с длиной, большей m, встречаются мало, то все серии длины m+1 объединяют в одну группу. Число серий этой группы обозначим K_m+1 . Получено p_m+1=10^-m , а критерий ² принимает вид:

.

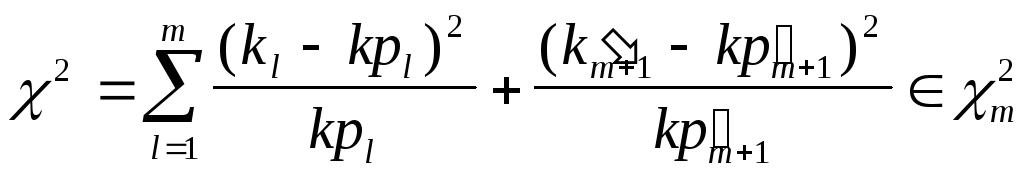Проверка равномерности. Для проверки гипотезы о равномерности распределения псевдослу­чайных чисел в интервале (0,1) обычно используется так называемый частотный тест. При этом гипотеза равномерности проверяется критерием . Интервал (0,1) разбивается на m равных интервалов. Да­лее определяется количество чисел , попавших в i -ыи интервал. Так как предполагаемое распределение равномерно, т.е. теоретические вероятности попадания в i- ый интервал равны , критерий можно записать в следующем виде:

.

Здесь n -число элементов исследуемой последовательности.

Проверка независимости. Для практического использования псевдослучайных чисел вполне достаточно их некоррелированности. Некоррелированность случайных чисел можно проверить с помощью коэффициента корреляции:

.

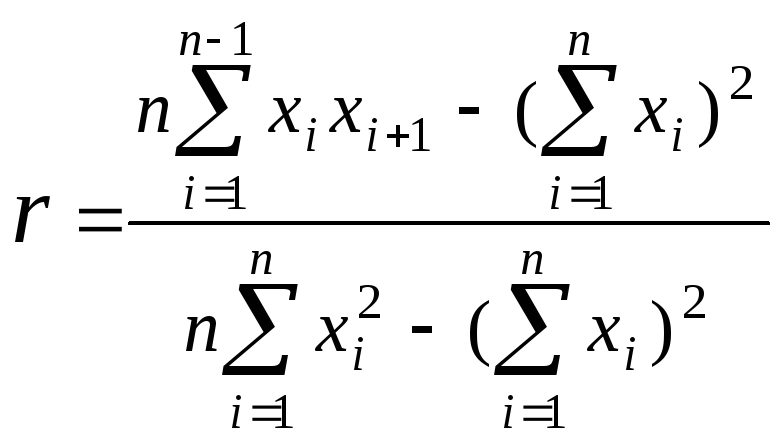Если полученное число близко к 0, то элементы последователь­ности считаются некоррелированными.

Например, если

,

то можно считать, что генератор выдержал тест.

2.3.5. Имитация случайных событий

Если требуется имитация случайного события А , наступающего с вероятностью p, то очевидно, что Р(А) совпадает с ве­роятностью , где - случайное число из равномерной в интервале (0,1) последовательности:

.

Это следует из того, что функция распределения равномерной в (0,1) величины Х есть

.

Следовательно, событию соответствует событие в том смысле, что

.

Отсюда легко видна схема имитации случайного события. Сначала генерируется псевдослучайное число , для которого проверяется выполнение неравенства . Если неравенство выполняется, то считается, что событие А наступило, в противном случае – нет. Такая схема имитации называется имитацией по жребию.

Эта схема может быть обобщена на группу событий. Пусть требу­ется смоделировать полную группу попарно несовместных событий , вероятности которых , где . Очевидно, что событие можно определить как выполнение двойного неравенства

,

так как тогда

.

Имитируя полную группу, мы считаем события несовместными. Рассмотрим теперь способ имитации совместных событий, не­зависимых и зависимых.

Допустим, требуется имитация двух независимых совместных со­бытий с вероятностями соответственно и . Здесь возмо­жны два подхода. В первом имитируются два псевдослучайных числа и , с помощью которых независимо друг от друга имитируются два события (по ) и (с помощью ). Тогда, если , то произошло, если еще , то и ; если но, , то ; если , но , то ; если , , то .

Второй путь предполагает имитацию по ранее приведенной схеме группы попарно несовместных событий , , , с вероятностями соответственно , , , .

Аналогичный подход используется в случае, когда совместные события и являются зависимыми. В этом случае для их имитации должны быть заданы три вероятности: , и . Еще одна вероятность вычисляется с помощью формулы полной вероятности:

,

откуда

.

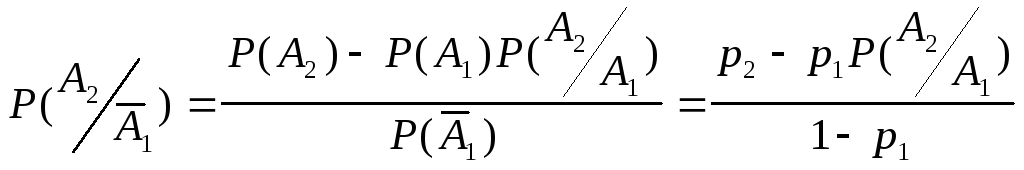При имитации зависимых совместных событий и тоже существу­ет два подхода. В первом случае генерируются два псевдослучайных числа и и имитируются события (по ) и (по ).

Второй вариант решения предполагает имитацию полной группы по­парно несовместных событий , , , .

Первый вариант опять предполагает меньшее число сравнений и в этом смысле является более экономичным.

2.3.6 Имитация случайных величин

Для имитации случайные величины должны быть заданы в виде сво­их распределений: случайная дискретная вели­чина – ряд или функция распределения, непреры­вная – функция распределения или плотность вероятности. При этом предполагается, что область определения случайной величины конечна, в противном случае для нее должно быть построено усеченное распре­деление, с помощью которого производится имитация. Усечение произ­водится следующим образом.

Если Y есть дискретная случайная величина, заданная распределением вида , то соответствующее усеченное распределение примет вид:

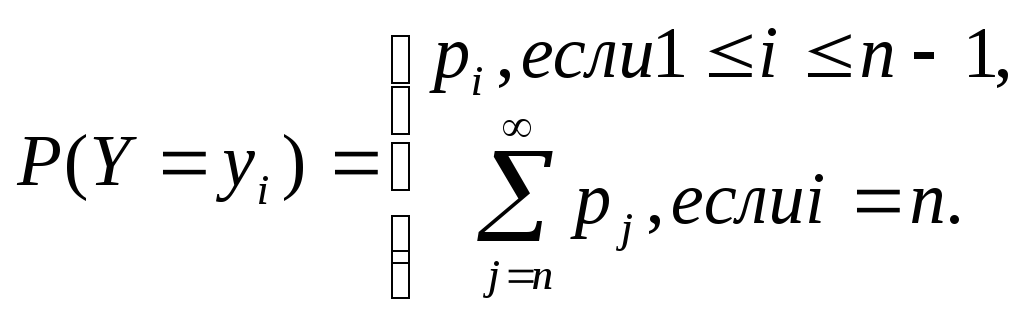
Если Y - непрерывная случайная величина с плотностью , где , то плотность вероятности соответствующего усеченного распределения имеет вид:

,

где .

Имитация дискретных случайных величин, заданных рядом распределения. Имитация дискретных случайных величин производится по аналогии с имитацией событий. Допустим, что нужно смоделировать случайную величину Y, заданную следующим рядом распределения:

.

Определяется событие .

Очевидно, что события ,…, образуют полную группу попарно не­совместных событий. Отсюда следует способ имитации дискретной слу­чайной величины, заданной рядом распределения.

Для имитации двух дискретных случайных величин и с за­данными распределениями можно использовать процедуры имитации сов­местных зависимых и независимых событий.

Имитация случайных величин, заданных функцией распределения. Имитация случайных величин, заданных функцией распределения, может быть выполнена с помощью точных или приближенных методов. Из точных методов наиболее распространен метод обратной функции, который базируется на следующей теореме.

Теорема 1

Пусть – функция распределения некоторой случайной величи­ны, а X – случайная величина, равномерно распределенная в (0,1). Тогда случайная величина, определенная соотношением , где - функция, обратная , имеет функцию распределе­ния .

Из теоремы 1 вытекает следующий способ преобразования случай­ных чисел с равномерным в интервале (0,1) распределением в последовательность случайных чисел с функцией распределения F(y). Для получения значе­ния у случайной величины , функция распределения которой F(y), нужно из последовательности псевдослучайных чисел выбрать одно x и разрешить относительно у уравнение

. (2.7)

Полученное решение и есть искомое число.

Примеры.

1. Имитация экспоненциальной случайной величины

Плотность вероятности

Функция распределения

.

Тогда уравнение (2.7) запишется в виде

,

откуда

.

Если x распределено равномерна в интервале (0,1), то 1-x тоже имеет равномерное в (0,1) распределение, т.е. можно записать

.

2. Имитация случайной величины, распределенной по закону Паскаля

Функция распределения случайной дискретной величины, распределенной по закону Паскаля, имеет вид

.

Значениями величины y являются 0,1,2,...

Очевидно, что решение уравнения (2.7) запишется так:

.

Так как у должно быть целым, считаем

.

Имитация непрерывной случайной величины, методом Неймана (исключения). Метод Неймана состоит в том, что из равномерно распределенной последовательности отбираются случайные числа, удовлетворяющие некоторому условию таким образом, чтобы отобранные числа имели заданный закон распределения.

Теорема 2

Случайная величина имеет плотность вероятности g(x), если

_.

Метод Неймана, базирующийся на теореме 2, формулируется следующим образом:

1. из исходной совокупности псевдослучайных чисел выбираются пары

;

2. для этих чисел проверяется справедливость условия

; (2.8)

3. если неравенство (2.8) выполняется, то очередное значение случайной величины Y, имеющей плотность распределения f(y), получено:

.

Методом Неймана целесообразно пользоваться, если f(y)=0, когда и легко подсчитывается на . Недостатком метода является то, что он приводит в среднем к отброшенным точ­кам.

Пример.

Требуется получить случайные числа, распределенные с плотнос­тью вероятности следующего вида:

.

При этом .

Условие (2.8) имеет вид

.

и при этом

.

Имитация нормального распределения. На основе центральной предельной теоремы можно построить алго­ритм имитации нормальной случайной величины с математическим ожида­нием a и дисперсией . Для этого достаточно просуммировать M равномерно распределенных случайных чисел. Процедура получается особенно простой, если в качестве М взять число 12. При этом, сум­мируя 12 псевдослучайных чисел, в соответствии с центральной предельной теоремой получаем нормально распределенную случайную ве­личину z с параметрами . Преобразуя z следующим обра­зом:

,

мы получаем искомую величину Y с математическим ожиданием a и дисперсией .

Имитация распределения Эрланга порядка (-распределение). Плотность вероятности – распределения имеет вид

.

Распределение Эрланга – это распределение суммы К независимых случайных величин, каждая из которых распределена по экспоненциаль­ное закону с параметром . Так как методом обратной функции экспоненциальную случайную величину можно имитировать с помощью выра­жения

,

то случайную величину, распределенную по закону Эрланга, можно по­лучить, вычисляя выражение

.

Распределения имитируются с помощью процедуры имитации нормальной случайной величины. Известно, что если и взаимно независимы, то , т.е. для имитации распределе­ния достаточно просуммировать квадраты нормальных величин.

Если , а , и Y не зависит от Z, то

.

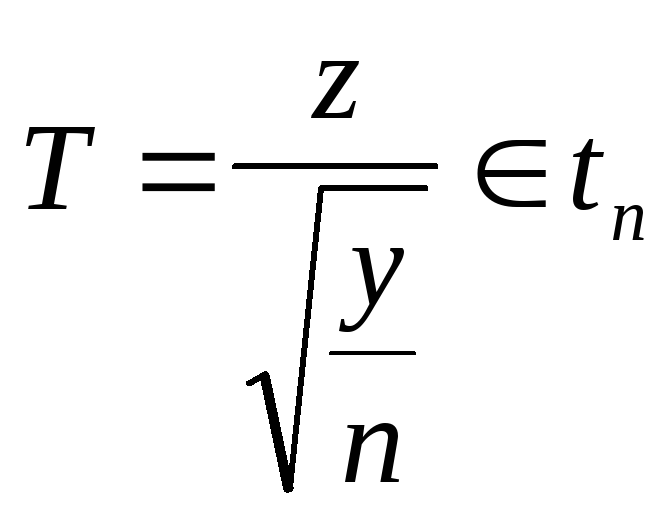Наконец, если и Z и Y независимы, то

.

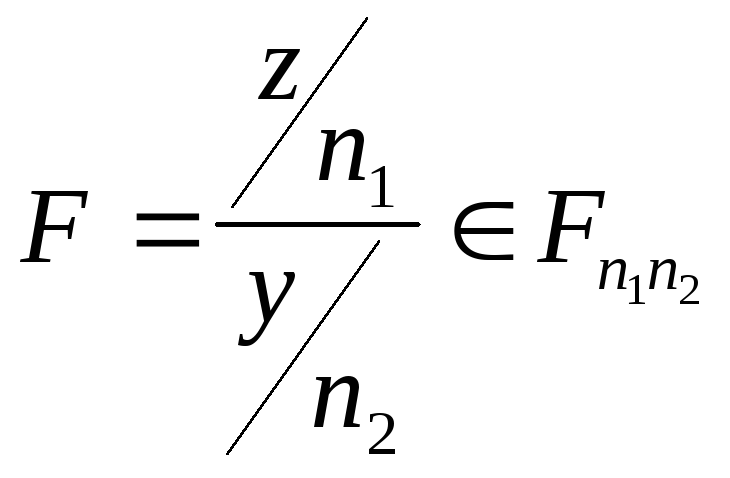Имитация случайных потоков. Как правило, потоки событий имитируются с использованием распределений случайного времени между двумя соседними событиями. Если рассматриваемый поток является стационарным и известна плотность или функция распределения времени между событиями, то методами имитации случайных величин вычисляются значения случайного времени между событиями. Тогда момент наступления i-го события вычисляется по формуле

_.

При этом должно быть задано. Если поток является нестационарным, то для формирования каждого используется свой закон распределения.

Если поток событий является многомерным, то процедура имитации осуществляется методами имитации случайных векторов. При этом, получив случайный вектор и определив моменты наступления событий

_,

следует упорядочить события потока по времени наступления.

Если многомерный поток является стационарным и ординарным с .многомерной плотностью , то его можно имитировать следующим образом. Моделируется одновременный поток событий с плотностью принадлежность события i-й составляющей потока определя­ется по жребию с вероятностью

.

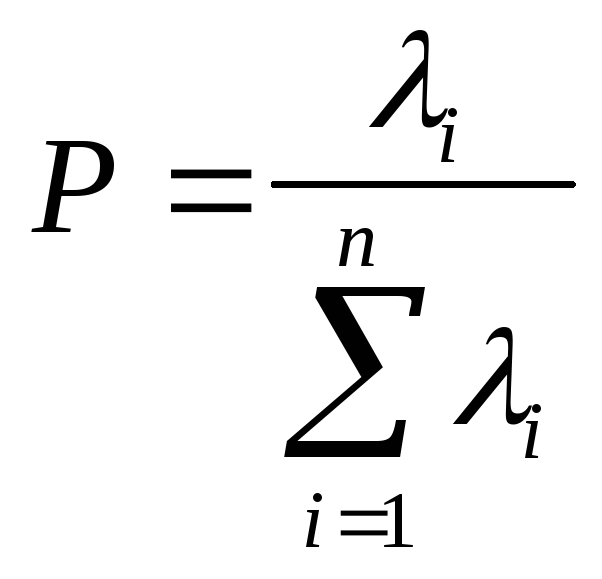При этом есть величина, обратная среднему времени между заявками.