3.2.Методы исследования смо с простейшими потоками заявок

Этот тип СМО наиболее изучен и просто описывается математическими выражениями. Считается, что все потоки, циркулирующие в СМО, являются простейшими: входной поток, поток уходов, поток выталкиваний, поток отказов, поток обслуживания и выходящий.

3.2.1.СМО с отказами

Этот тип СМО отличается тем, что отсутствует очередь, поэтому заявка, пришедшая в систему и заставшая все каналы обслуживания занятыми, получает отказ и покидает систему не обслуженной.

Дисциплины ожидания и обслуживания считаются бесприоритетными.

Одноканальная СМО с отказами. Наиболее простой системой является одноканальная СМО с отказами – М/М/1. Она имеет один канал обслуживания, входящий поток характеризуется интенсивностью , поток обслуживания – интенсивностью . Основными характеристиками такой системы являются абсолютная и относительная пропускная способность.

Абсолютная пропускная способность – это интенсивность выходящего потока обслуженных заявок (_об).

.

Для того, чтобы определить СМО, нужно: обозначить все её состояния и их количество, задать интенсивность всех возможных переходов между состояниями и начальное состояние.

Рассматриваемая СМО имеет всего два состояния: Z₀ – система свободна, заявок нет, канал обслуживания простаивает; Z₁ – в системе находится одна заявка, которая занимает канал обслуживания, это состояние занятости системы.

В соответствии с таким заданием системы её граф будет иметь вид, показанный на рис. 3.5





Рис. 3.5

Переходу из состояния Z₀ в Z₁ соответствует поступление заявки на вход системы с интенсивностью , а переходу из Z₁ в Z₀ соответствует выход обслуженной заявки из системы. С интенсивностью обслуживания .

Уравнение Колмогорова можно записать так:

; ;

Учитывая условие нормировки и стационарный режим работы СМО, получим: ;

Из этой системы определяются вероятности P₀ и P₁: ; ;

Так как P₀ – это вероятность простоя системы, одновременно это и вероятность того, что система может принять заявку на обслуживание, т.е. вероятность обслуживания P₀=P_об; а P₁ – это вероятность занятости канала, одновременно это и вероятность того, что СМО не может принять новую заявку на обслуживание, т.е. вероятность отказа P₀=P_отк;

Многоканальная СМО с отказами. Система характеризуется отсутствием очереди, наличием m каналов обслуживания, причём все каналы обслуживают заявки с одинаковой интенсивностью , т.е. являются универсальными. Входящий поток имеет интенсивность , заявки бесприоритетные. Как и в предыдущем случае состояния такой системы определяются количеством связных с ней заявок, т.е.:

Z₀ – заявок нет система свободна;

Z₁ – в системе находится одна заявка, занимающая один канал обслуживания;

…

Z_m – в системе находятся m заявок, занимающие все каналы обслуживания.

Переходы между состояниями Z₀-Z₁-Z₂-… происходят под воздействием входящего потока заявок с интенсивностью . Переходы Z_m-Z_m-1-… происходят под воздействием потока обслуженных заявок, с интенсивностью пропорциональной числу каналов обслуживания.

Граф состояний системы имеет вид (рис. 3.6.)

  . . . .   . . . . 

. . . . . . . .

 2 k (k+1) m

Рис.3.6.

По графу составляются система уравнений Колмогорова:

Поскольку граф представляет собой модель размножения и гибели, для нахождения вероятностей состояний можно использовать формулы Эрланга:

;

;или;

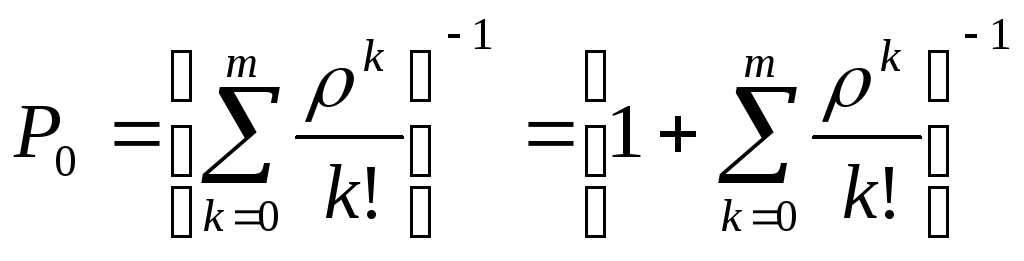
где - приведённая интенсивность входящего потока, - число заявок, поступающих на вход системы за время обслуживания одной заявки; для системы в стандартном режиме всегда <1.

Характеристиками данной системы являются:

1. вероятность отказа, то есть вероятность того, что все каналы

заняты: ;

2. вероятность обслуживания P_об=1-P_отк=1-P_m;

3. абсолютная пропускная способность: ;

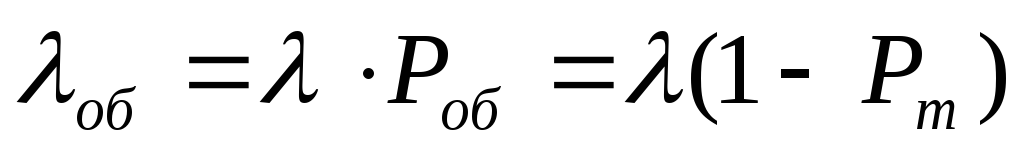4. среднее число занятых каналов; его можно рассматривать как интенсивность потока обслуженных заявок, отнесённую к интенсивности обслуживания: ;

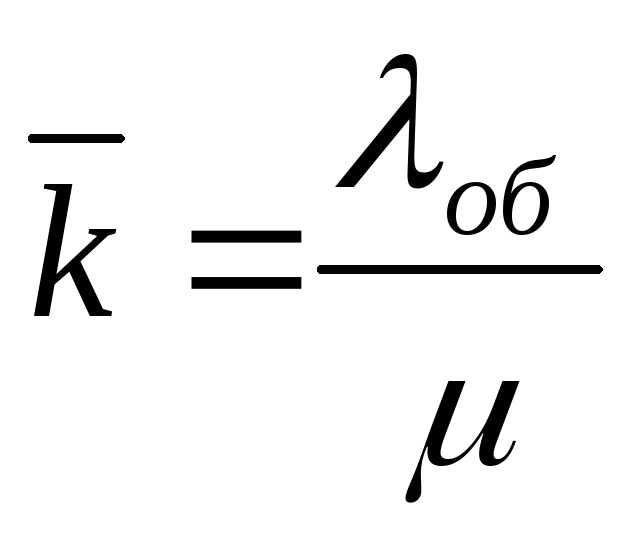5. загрузка канала – среднее число занятых каналов, отнесённое к количеству каналов: .

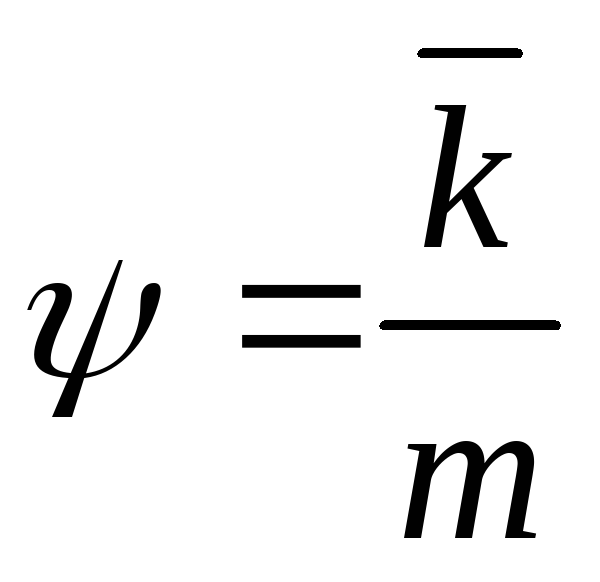3.2.2.СМО с ожиданием

Этот вид СМО характеризуется наличием очереди, т.е. , поступившая на вход системы заявка, либо сразу назначается на обслуживание, если хотя бы один канал свободен, либо, в противном случае, становится в очередь с числом мест n, заявка получает отказ и покидает систему не обслуженной только в том случае, если все каналы обслуживания и очередь заняты. Дисциплины ожидания и обслуживания считаются бесприоритетными.

Одноканальная СМО с ожиданием (М/М/1).

Поток входящих заявок пуассоновский с интенсивностью , интенсивность обслуживания .

Такая система может находиться в (n+2) состояниях:

Z₀ – система свободна, очереди нет, канал обслуживания простаивает;

Z₁ – одна заявка находится в канале обслуживания, очереди нет;

.

.

.

Z_n+1 – одна заявка находится в канале обслуживания и в очереди находятся n заявок.

Граф переходов описанной системы показан на рис.3.7.

  . . . . .   . . . . . 

. . . . . . . . .

    

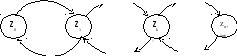
Рис.3.7.

Данная модель - это частный случай модели, «размножения и гибели», поэтому для нахождения вероятностей состояний используются формулы Эрланга:

; и .

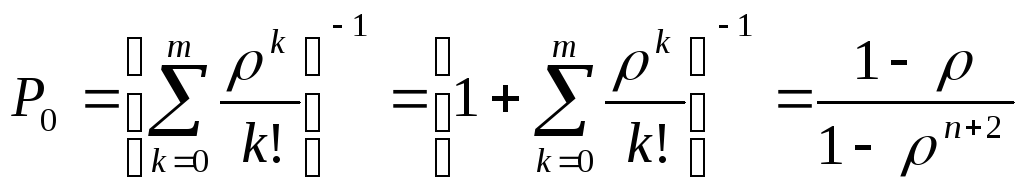Основные характеристики данной системы:

1. вероятность отказа – это вероятность того, что единственный канал обслуживания и n мест в очереди заняты т.е. это вероятность состояния Z_n+1:

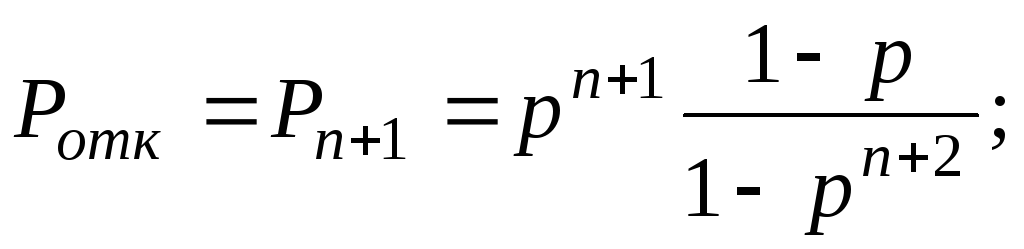
2. вероятность обслуживания или относительная пропускная способность: ;

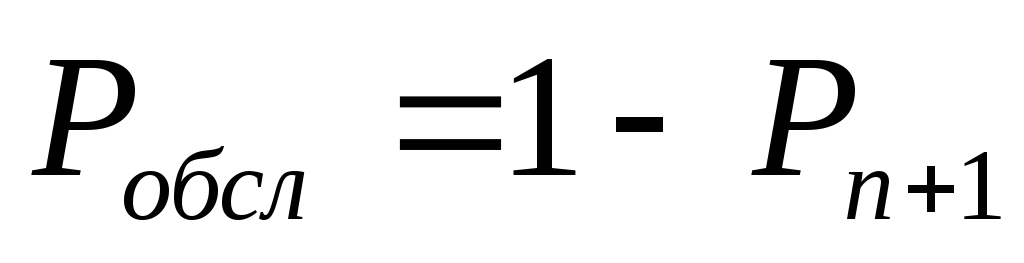3. абсолютная пропускная способность – интенсивность покоя обслуженных заявок: ;

4. средняя длина очереди определяется по стандартной формуле для математического ожидания дискретной случайной величины с учётом вероятностей состояний и связи номера состояния с числом мест в очереди:

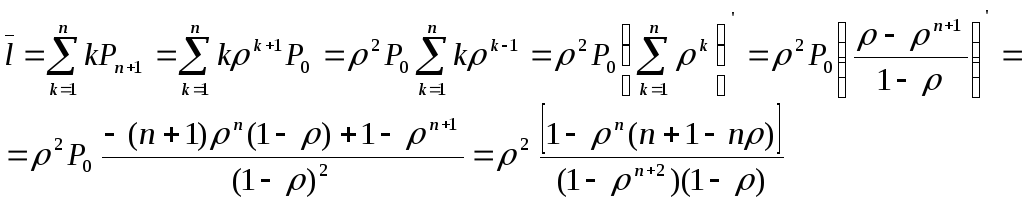
5. среднее число заявок в системе: ;

6. среднее время ожидания:

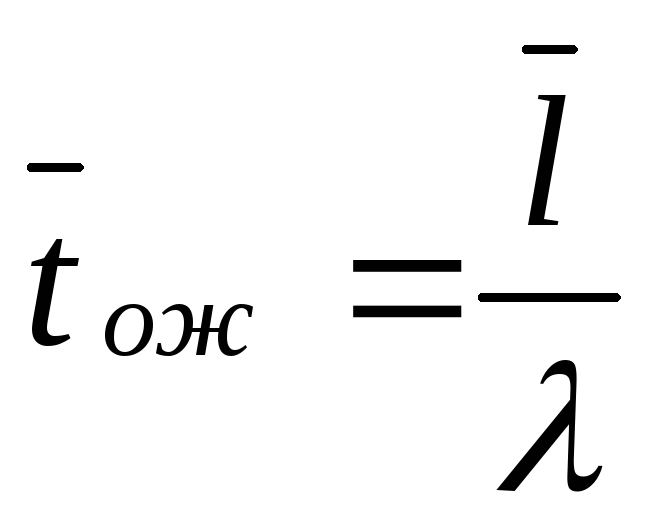
Если СМО имеет неограниченную очередь (), то стационарный режим устанавливается только при выполнении условия <1, т.к. в противном случае очередь неограниченно возрастает. Если же <1, то и .

При бесконечной очереди любая заявка, поступившая в систему обязательно будет обслужена, поэтому абсолютная пропускная способность равна λ. Характеристиками таких СМО являются:

1. вероятность отказа - P_отк=0;

2. вероятность обслуживания - P_об=1 ;

3. средняя длинна очереди: - ;

4. среднее время ожидания - ;

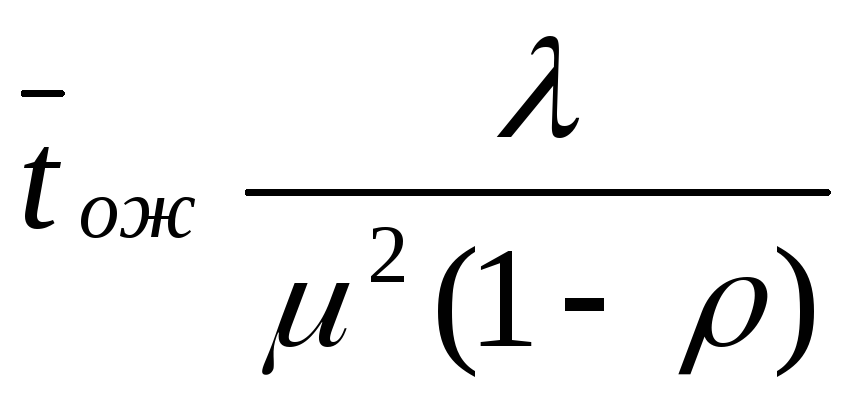5. среднее число заявок в системе - ;

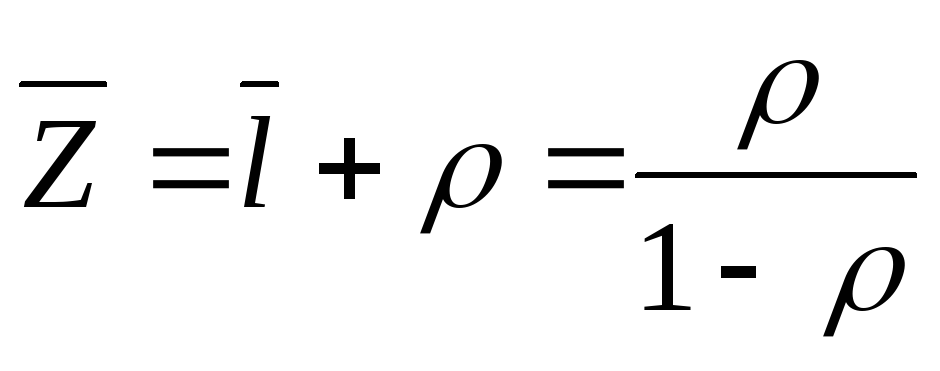6. среднее время пребывания заявки в системе - .

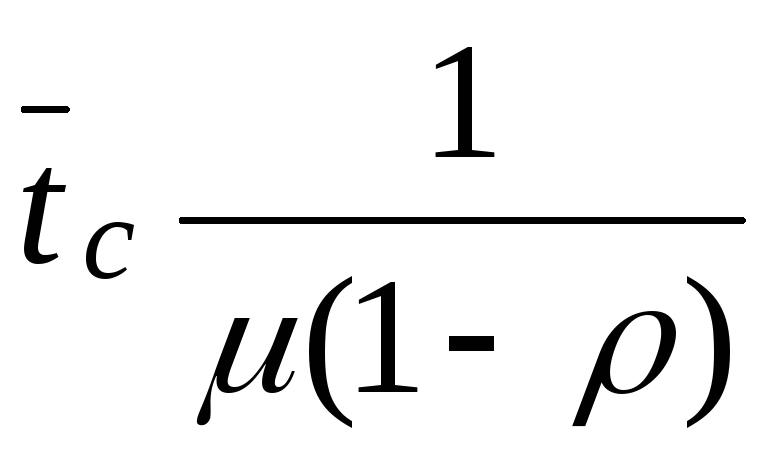Многоканальная СМО с ожиданием (М/М/m).

В системе имеется m каналов обслуживания и очередь с числом мест n, с каждого из которых заявка может поступать на любой освободившийся канал. Все потоки заявок, циркулирующие в системе – простейшие, с экспоненциальным законом распределения интервалов времени. Интенсивность входящего потока -  заявок/ед.вр, интенсивность потока обслуживания  заявок/ед.вр. Дисциплины ожидания и обслуживания бесприоритетные. Заявка, поступившая на вход системы назначается на обслуживание, если хотя бы один из m каналов свободен. Если каналы обслуживания заняты, заявка поступает в очередь и ждёт начала обслуживания. Если все n мест в очереди заняты, заявка получает отказ и уходит из системы не обслуженной. Как и прежде, будем связывать состояние системы с числом находящихся в ней заявок, т.е.:

Z₀ – состояние простоя (нет заявок, каналы простаивают, очередь отсутствует);

Z₁ – в системе одна заявка, её обслуживает один канал, остальные (m-1) каналов свободны; очереди нет;

…..

Z_m – очереди ещё нет, в СМО m заявок, все каналы заняты обслуживанием;

Z_m+1 – все m каналов обслуживания заняты и одна заявка находится в очереди;

…..

Z_m+n – все m каналов обслуживания заняты и все n мест в очереди заняты;

В состоянии Z_m+n система не способна принять ни одной заявки, все вновь пришедшие заявки получат отказ.

Переходы между состояниями будут происходить под действием входящего потока заявок и потоков обслуживания.

Граф состояний системы показан на рис.3.8.

  . . . . .   . . . . . 

. . . . . . . . .

 2 m m m

Рис.3.8.

Если все каналы заняты, интенсивность обслуживания равна m, в противном случае она пропорциональна количеству каналов, занятых обслуживанием.

Данная модель относится к модели «Размножения и гибели», поэтому для определения вероятностей состояния системы можно использовать формулы Эрланга:

; 1≤k≤m;

; k>m;

.

Характеристиками данной системы являются:

1. вероятность отказа – это вероятность того, что пришедшая в систему заявка получит отказ, т.е. это вероятность состояния Z_m+n: ;

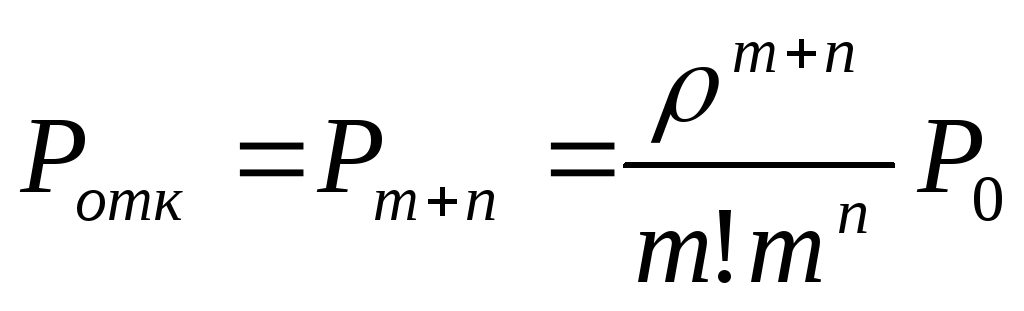2. вероятность обслуживания или относительная пропускная способность: ;

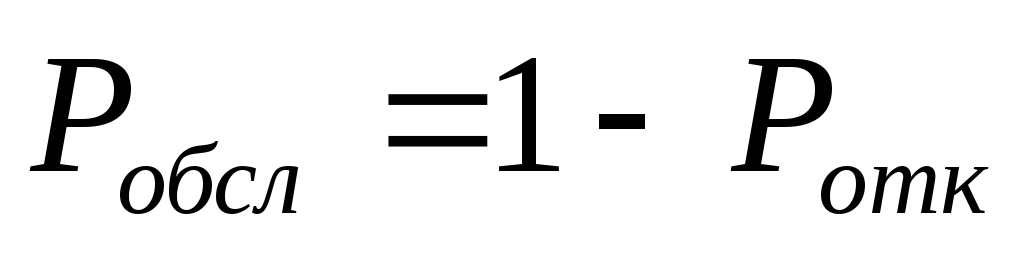3. абсолютная пропускная способность или интенсивность потока обслуживания: ;

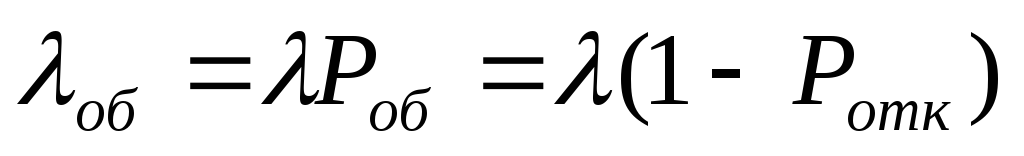4. средняя длина очереди:

5. среднее время ожидания заявки в очереди – t_ож. Для определения t_ож необходимо рассмотреть всевозможные гипотезы о том, в каком состоянии застанет систему вновь прибывшая заявка и сколько времени ей придётся ждать обслуживания с учётом бесприоритетных дисциплин ожидания и обслуживания. В частности, если заявка застанет систему в одном из состояний Z₀, Z₁,… Z_m-1, когда очередь и каналы свободны, ей не придётся ждать начала обслуживания и t_ож =0. Если заявка застает систему в состоянии Z_m, когда все каналы заняты обслуживанием, заявка занимает первое место в очереди и ждёт окончания обслуживания в одном из каналов.

Суммарный поток обслуживания при полностью загруженных каналах складывается из m простейших потоков обслуживания с одинаковой для всех каналов интенсивностью , следовательно, суммарный поток имеет интенсивность m. Время ожидания заявки в среднем равно , причём, вероятность этого события P_m. Если вновь пришедшая заявка застаёт систему в состоянии Z_m+1, она занимает второе место в очереди и будет ждать в среднем единиц времени. В состоянии Z_m+n-1, когда СМО ещё может принять заявку, время ожидания заявки равно

В состоянии Z_m+n заявка получает отказ и время ожидания равно нулю t_ож=0. Среднее время ожидания можно найти по формуле математического ожидания для дискретной случайной величины:

6). - среднее время пребывания заявки в системе;

7) - среднее число заявок в системе;

8) среднее число занятых каналов: ..

Если принять длину очереди неограниченной , любая заявка, поступившая на вход системы, рано или поздно будет обслужена («Чистая» СМО).

Предельные вероятности состояний:

(k=1,2,…,m);

(l=1,2,…,);

.

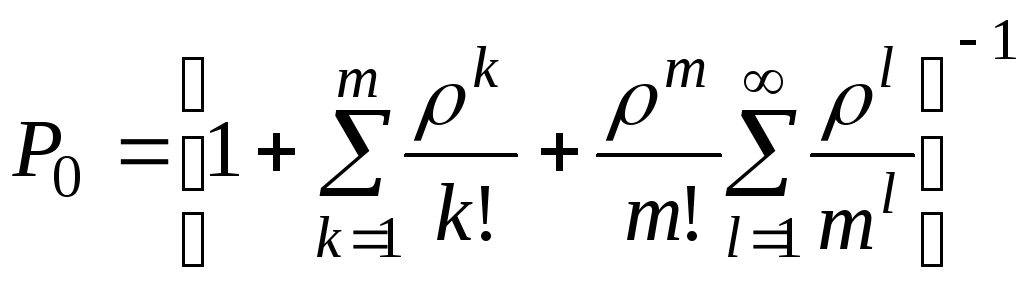Установившийся режим в такой системе существует, если ,

т.к. в противном случае каналы обслуживания не будут справляться с потоком заявок очередь будет неограниченно возрастать.

При и формулы для характеристик существенно упрощаются:

.

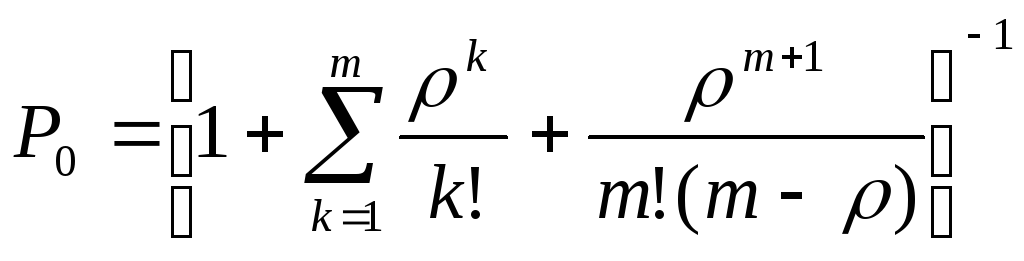В «чистой» СМО потери отсутствуют, поэтому P_об=1, _об=, Р_отк=0;

• среднее время ожидания ;

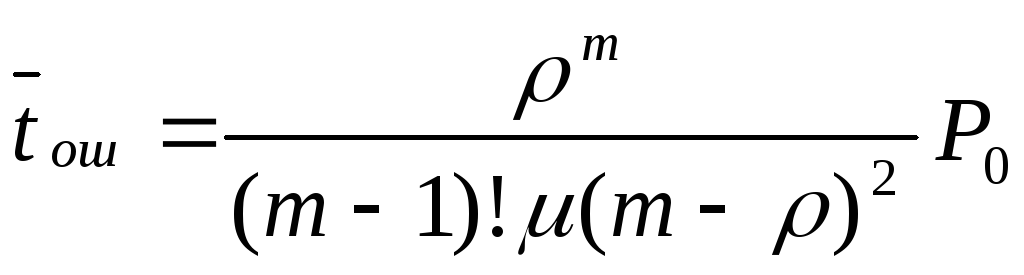• среднее время обслуживания ;

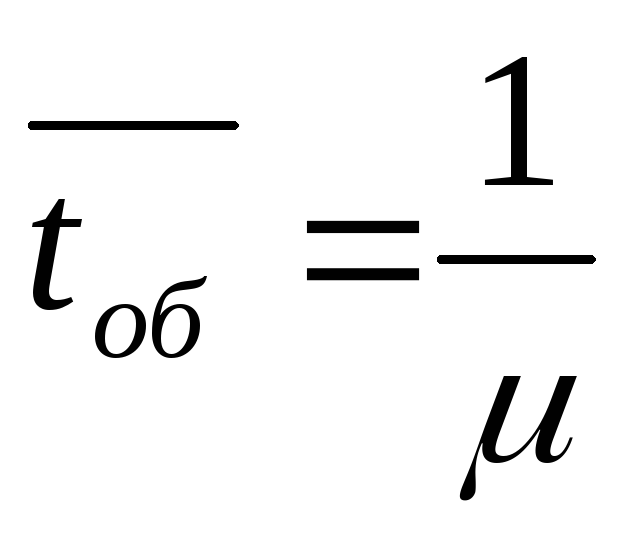• среднее время пребывания заявки в системе ;

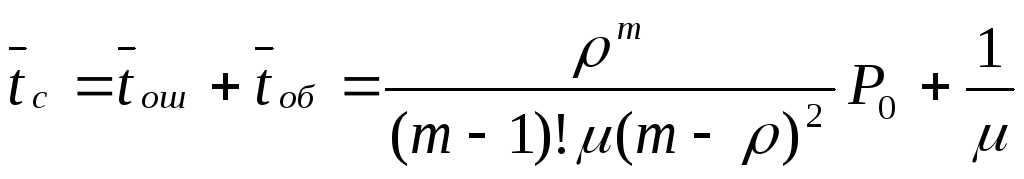• средняя длина очереди ;

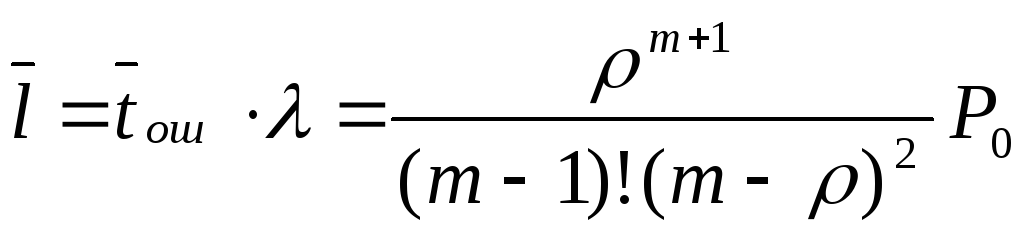• среднее число занятых каналов .

Полученные соотношения удобны в том случае, когда число мест в очереди значительно превышает среднюю длину очереди.

3.2.3.СМО с «нетерпеливыми» заявками

На практике часто встречаются СМО, в которых заявки могут уйти из системы, не дождавшись начала обслуживания или во время обслуживания, если время пребывания в системе превышает некоторую величину τ_доп (заявка находится в СМО до тех пор, пока τ_доп > t_ож или τ_доп > t_с).

Для вычислительных систем примером такой ситуации может служить старение информации.

В

ремя τ_доп ‑ допустимое время пребывания заявки в системе. Предполагается, что поток уходов является простейшим со средним τ_доп . Т.к. для простейшего потока исчерпывающей характеристикой является интенсивность, для потока уходов “нетерпеливых” заявок

можно ввести интенсивность ν = . Заявки могут уходить как из очереди, если t_ож > τ_доп, так и из каналов обслуживания, если t_ож ≤ τ_доп. Обычно считается, что интенсивности этих уходов одинаковы и составляют ν_ож = ν_об = ν = . В качестве базовой модели для СМО с «нетерпеливыми» заявками выберем M/M/m с ожиданием. Процессы в системе определяются входящим потоком заявок с интенсивностью λ, потоком обслуживания с интенсивностью μ, потоком уходов из очереди с интенсивностью ν_ож из каналов обслуживания с интенсивностью ν_об.

Граф системы показан на рисунке 3.9.

…

…

λ λ λ λ λ

…

…

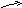
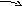
1(μ+ν_об) 2(μ+ν_об) m(μ+ν_об) m(μ+ν_об)+1ν_ож m(μ+ν_об)+nν_ож

Рис.3.9.

Переходы из состояний, соответствующих отсутствию очереди, в соседние слева состояния происходят под воздействием двух независимых потоков событий: потока обслуживания с интенсивностью μ и потока ухода «нетерпеливых» заявок с интенсивностью ν_об. Т.к. процессы в различных каналах обслуживания независимы, суммарная интенсивность переходов связана с числом занятых каналов и равна k( μ + ν_об). Интенсивность переходов при наличии очереди складывается из 2-х составляющих:

суммарной интенсивности переходов за счет потоков обслуживания и уходов заявок из каналов ‑ m( μ + ν_об) и суммарной интенсивности переходов за счет независимых уходов «нетерпеливых» заявок из очереди и пропорциональной длине очереди n.

Т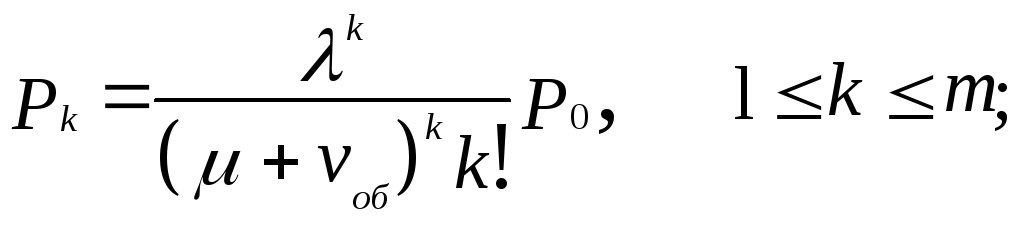 .к. граф на рис.3.9. – модель «размножения и гибели», используются формулы Эрланга для нахождения вероятностей состояний:

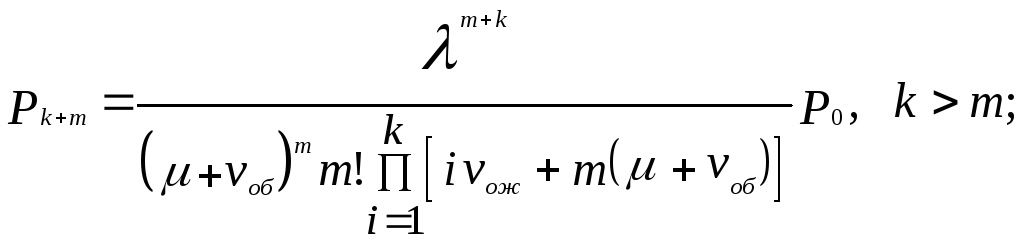
Е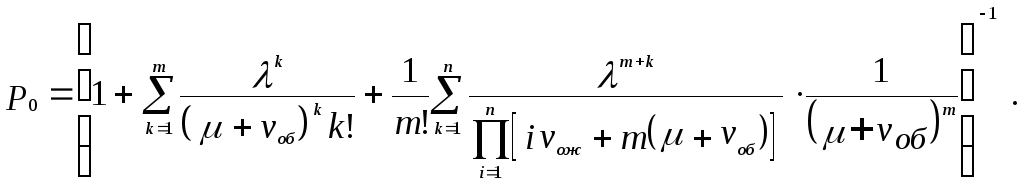 сли привести интенсивность уходов из очереди и из каналов к интенсивности обслуживания:

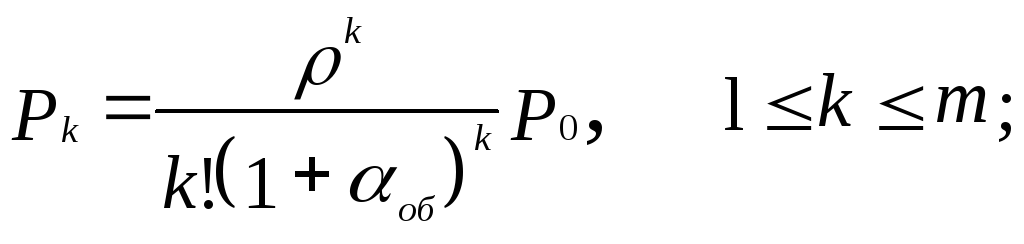
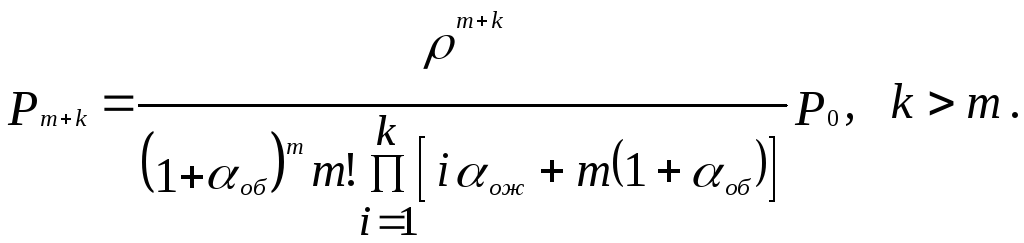
В ероятность P₀, определяемая из условия нормировки,

В данной СМО потери заявок возможны либо за счет отказов вследствие переполнения системы, либо в форме ухода «нетерпеливых» заявок из системы.

Определяющей характеристикой системы является не вероятность отказа, а вероятность потерь.

В 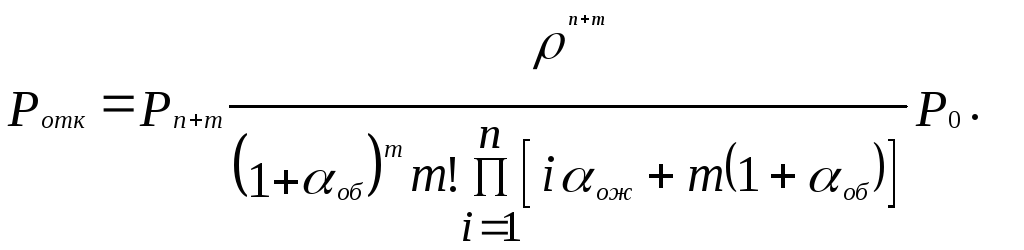ероятность отказов можно определить как вероятность состояния Z_m+n:

Т к. уходы заявок из очереди и каналов обслуживания – несовместимые события, то:

И з общих формул для характеристик можно получить характеристики СМО следующих частных случаев:

• з аявка может покинуть систему во время обслуживания

• заявка может покинуть систему, находясь в очереди

(прерывания обслуживания не допускается)

Остальные характеристики СМО определяются, как и в предыдущих случаях:

3.2.3.Замкнутые СМО

Замкнутые СМО отличаются тем, что число заявок, циркулирующих в них, постоянно, и характеристики системы определяются не только числом заявок, находящихся в ней, но и состоянием системы в данный момент времени. Примером такой СМО может служить станция ремонта автомобилей, на которую с предприятий поступают транспортные средства. Чем больше их находится в ремонте, тем меньше поток поступающих на ремонт автомобилей.

Другим примером является вычислительная система, работающая в диалоговом режиме.

Z

система имеет M терминалов T₁, T₂, … ,T_M (рис.3.10), за каждым из которых находится пользователь, формирующий запросы на решение задач. После того, как один пользователь сформировал запрос, он не может более формировать запросы до тех пор, пока не получит ответ на свой вопрос. Причем, время, необходимое пользователю для формирования запроса, считается распределенным экспоненциально с математическим ожиданием T, что позволяет рассматривать пользователя как источник заявок с интенсивностью

Интенсивность потока заявок на входе системы будет определяться числом пользователей, которые в состоянии послать запрос.

Обслуживание пользователей производится m каналами (m ≤ M), которые являются универсальными каналами обслуживания с известным математическим ожиданием длительности обслуживания и интенсивностью µ. В системе имеется n‑местная очередь, в которую поступают заявки, заставшие каналы обслуживания занятыми (n=M-m).

Граф переходов замкнутой СМО приведен на рис.3.11. Состояния системы определяются так:

T₁

T₂

T_M

k₁

k_m

…

M

O

…

n

…

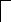
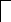
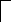
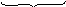
Рис.3.10.

Z₀ – заявок нет, ЭВМ простаивают, следовательно, интенсивность входящего потока равна Mλ;

Z₁ – одна заявка на обслуживании, очередь пуста; т.е. пользователь, пославший запрос, ждет ответа, следовательно, интенсивность потока заявок равна (M-1)λ;

. . .

Z_m – m пользователей отправили запрос, очереди еще нет, все каналы заняты; интенсивность потока заявок ‑ (M-m)λ;

Z_m+1 – (m+1) пользователь сформировал запрос, 1 заявка в очереди; интенсивность потока заявок – [M-(m-1)]λ;

. . .

Z_m+n – все M пользователей сформировали запрос, система полностью загружена, интенсивность входящего потока равна 0.

…

…

Mλ (M-1)λ [M-(m-1)]λ (M-m)λ λ

…

…

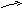
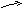
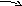
μ 2μ mμ mμ mμ

Рис.3.11.

В системе существует установившийся режим. Т.к. граф соответствует схеме «размножения и гибели», то для определения предельных вероятностей состояний можно воспользоваться формулами Эрланга:

Для случая, когда имеется очередь:

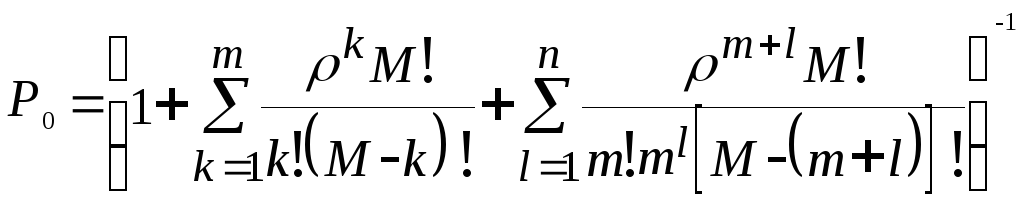
Характеристики данной системы:

1) поскольку система является замкнутой, то все заявки обслуживаются и

2) вероятность обслуживания ‑

3) абсолютная пропускная способность рассматривается как суммарная производительность каналов обслуживания –

4

) для определения среднего числа заявок находящихся в системе, используется условие равенства в установившемся режиме интенсивности выходящего потока и потока заявок на входе системы:

5) средняя длина очереди ‑

6

) для нахождения среднего времени ожидания выдвигаются гипотезы о значении времени ожидания поступившей заявки в различных состояниях системы. Для математического ожидания

В

состояниях от Z₀ до Z_m-1 вновь прибывшая заявка немедленно назначается на

обслуживание и В В состоянии Z_m заявка ожидает обслуживания в течении

течении времени Для произвольного состояния это время

равно

Таким образом:

7 ) среднее время нахождения заявки в системе:

рассматривается как среднее время, в течении которого пользователь ждет ответа на запрос;

8) среднее число занятых каналов можно найти как математическое ожидание числа занятых каналов –