24. Метод построения переходных процессов в сау с помощью трапецеидальных вчх.

Последов. расчетов: 1-й шаг: представл. график ВЧХ в виде горизонт. и наклонных линий. 2-й шаг: из этих отрезков составл. трапеции, которые одной

примыкают к оси ординат. 3-й шаг: перемещаем трапеции чтобы их основания оказались на оси абцисс.

Чтобы сумма площадей трапеции приближалась к площади под кривой ВЧХ, площадь I берем со знаком “+”, II-III cо знаком “-“.

P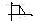(ω)= Σⁿ_i=1P_i(ω)- трапецеид. ВЧХ. H(t)= 2/П ∫^∞₀(P(ω)*sinωt/ω)*dω=Σh_i(t)+∆h(t)= наибольшая погрешность апраксимации лежит в области высоких частот. Отброшенный высокочастотный хвост ВЧХ отразиться только на начальном участке перех-ой хар-ки. (ω→∞, t→0) =Σh_i(t). 4-й шаг: для каждой трапеции находим составл-ю перех. хар-ки. Для этого использ. таблицу так назыв. h-функций: h_i(t). Сначала опред. Параметры трапеции

а) r_i=P_i(0)- высота трапеции,

б) χ_i=ω_ai/ω_ci- коэф. наклона в интер-ле (0;1). Таблицы составл. для единичной трапеции P_i(0)=1 и для различных

к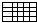оэфф. наклона χ_i=0;0.05;…;0.95;1. Таблицы составл. для безразмерного времени τ=ω_c(t). Из таблицы извлекаем значение перех-ой хар-ки. h¹_i(t)- еден. трапеция. Затем коорд. Времени: t_i= r_i/ω_ci, h_i(t)=r_i*h¹_i(t).

Повторяя вычисл. для других трапеций находим все составл-еh_i. строим график h_i с учетом знаков трапеции и графически

суммируем.

25. Временные показатели качества переходных процессов.

Для оценки поведения САУ переход. Режимов используются различ. показат. качества. Их делят на след. группы: 1) временные показат. качества, 2) частотные показат. качества, 3) интегральные показат. качества. Мы остановимся на временных:

1) Статическая ∆, 2)Max динамическое отклонение ∆Y_дин, 3) Перерегулирование δ=(∆У_уст/∆У(∞)) *100%, 4) время регулирования t_p, b=0.05*∆У(∞) или b=0.05* А₁,

5) степень колебательности m ( от1 до 3) колеб. 7) степень затухания т.е показывает

на сколько уменьшается амплитуда колебаний за 1 период.

Φ=0,7…0,9. В совокупности показатели качества создают определ. границы для протек. Переходного

процесса.

26. Частотные показатели качества процесса регулирования.

Качество системы определяется по частотным хар-ам разомкнутой или замкнутой системы. а) запас устойчивости по амплитуде и по фазе. Основана на критерии устойчивости Найквиста и отражает удаление АФХ от разомкнутой системы от крит. точки (-1;j0).

∆L=20Lga, a(∆L) –запас устойчивости по амплитуде, показывает на какую вел-ну может измениться модуль АФХ разомкнутой системы на частоте

п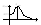ри кот. ФЧХ достигнет значения –П для того чтобы замкн. система оказалась на границе устойчивости. γ- запас устойчивости по фазе. Показыв. на какую вел-ну следует увел. отставание по фазе в разомкнутой системе на частоте которой А(ω)=1 иL(ω)=0дБ для того чтобы замкн. система оказалась на границе устойчивости. Считается что запас устойчивости равен: ∆L= 6…12дБ. (а=0,5..0,?). γ≥30⁰. б) показатель колебательности М. Считается что замкнутая система близка по своим св-ам свойствам колебательного звена.

Чем больше величена пика тем сильнее колеб. перех. процесса, тем меньше запас устойчив. М=А_max/А(0) 1.1<M<1.8 в)

ω_р- резонансная частота соотв. пику АЧХ. ω_n- частота пропускания системы. А(ω)>А(0)/√2. ω_c- частота среза системы. Частота среза раз. системы приблизит. будет равно ω_{резонан} у замкнутой системы и это позв-ет приблизительно оценить длит. перех. процесса. t₁≈П/ω_c. В правильно спроектир. системе переход. процесс заканчив. за 1-3 колеб. и тогда t_n≈(1…3)2П/ω_c. Чем шире полоса пропускания ω_п тем более быстродейтв. Будет система. г) Оценка качества по ВЧХ замкнутой системы.

(0;ω _n)- интервал положит. в котором P(ω)>0, (0;ω _с)- интервал существования частот в котором |P(ω)|≥0.1 P(0). Если при ω>ω _с,

P(ω)<0.2 P(0), то о качестве системы можно судить огран. интервале положительности. Вид ВЧХ позволяет оценить вид переходного процесса и его длительность. Если P(ω)>0 и производная dP(ω)/dω<0, то переходный процесс монотонный без перерегулирования.

Если ВЧХ имеет разрыв, то это свидетельствует о наличии автоколеб. с

частотой ω_i,

Наличие пиков говорит о колебат. перех. процесса, перерегулир. при этом приблиз. оценив. по эмпирической ф-ии:

σ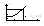%=(1,18P_max-Р(0))/Р(0).

Длительность перех. процесса приблизительно оценив. поP_max и ω_п.

t_n= t_n*ω_п/ω_п.