4. Дифференциальные уравнения сау. Уравнения статики. Линеаризация уравнений. Стандартная форма записи линейных дифференциальных уравнений.

В общем случае звенья и системы описывают нелинейными дифференциальными уравнениями произвольного порядка. Под звеном понимается математическая модель элемента. Для примера рассмотрим звено, которое можно описать дифференциальным уравнением второго порядка где y – выходная величина, u и f – входные величины, и – первые производные по времени, – вторая производная по времени.

Уравнение (2.1), описывающее процессы в звене при произвольных входных воздействиях, называют уравнением динамики. Пусть при постоянных входных величинах u = u⁰ и f = f⁰ процесс в звене с течением времени установится: выходная величина примет постоянное значение y = y⁰. Тогда (2.1) примет вид

Это уравнение описывает статический или установившийся режим и его называют уравнением статики

Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой звена или элемента (а также системы) называют зависимость выходной величины от входной в статическом режиме.

Главным упрощением, к которому следует стремиться при выводе уравнений звеньев системы, является их линеаризация, т. е. описание линейными дифференциальными уравнениями. Линеаризация нелинейности, содержащейся в уравнении звена, заключается в замене этой нелинейности приближенной линейной зависимостью

Другой формой записи линейных уравнений звеньев является запись с помощью передаточной функции. Уравнение (2.7) при этом принимает вид: (2.8или

В общем случае звено системы автоматического управления, имеющее п входов, описывается дифференциальным уравнением

(2.10) или в другом виде (2.11)

Здесьx_i — входные воздействия на звено (i = 1, 2, ..., n); Q(p) и R_i(р) — полиномы относительно р;

—передаточная функция звена для i-го входного воздействия.

Стандартная форма записи линейных дифференциальных уравнений. Обычно линейные дифференциальные уравнения с постоянными коэффициентами не выше второго порядка записывают в стандартной форме. При этом члены, содержащие выходную величину и ее производные, записывают в левой части уравнения, а все остальные члены — в правой; коэффициент при выходной величине делают равным единице. Если в правой части содержатся производные, то члены, со­держащие какую-либо одну входную величину и ее производные, объединяют в одну группу и коэффициент при соответствующей входной величине выносят за скобки.

Уравнение (2.26) в стандартной форме принимает вид (2.36)

Где

В уравнении (2.36) постоянные Т₀, Т₁ и Т₂ имеют размерность времени и их называют постоянными времени, а коэффициенты k₁ и k₂ — передаточными коэффициентами. Если исходное уравнение (2.26) не содержит y (a₂ = 0), то в стандартной форме коэффициент при производной y должен быть равен единице: обе части уравнения делят на коэффициент a₁.

6. Передаточные функции звеньев сау, их связь с дифференциальными уравнениями

Отношение оператора воздействия к собственному оператору называют передаточной функцией или переда­точной функцией в операторной форме. Звено, описываемое уравнением (2.26)

или, что тоже самое, уравнениями (2.27) — (2.29), можно характеризовать двумя передаточными функциями: передаточной функцией W₁(p) по входной величине и, т. е. (2.30)

и передаточной функцией W₂(p) по входной величине f, т.е.

(2.31)

Используя передаточные функции, уравнение (2.26) записывают в виде

(2.32)

Уравнения (2.28), (2.29) и (2.32) называют уравнениями в символической или операторной форме записи.

П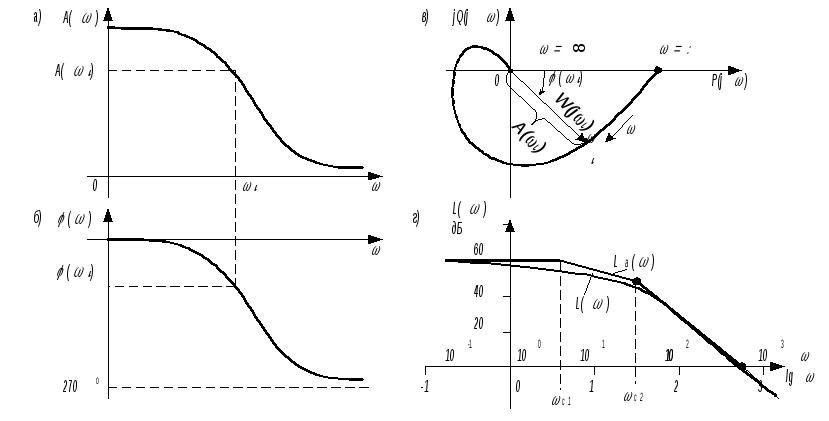ередаточной функцией или передаточной функцией в форме изображений Лапласаназывают отношение изображения выходной вели­чины к изображению входной величины при нулевых начальных условиях. Если звено (система) имеет несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные входные величины полагают равными нулю.