38. Основные виды фазовых траекторий линейных систем второго порядка.

Уравнение системы второго порядка:

Корни этого уравнения:

Для разных значений a возможны шесть разных случаев, следовательно шесть фазовых траекторий.

1. корни чисто мнимые при a₁=0, а₂>0 (колебательная граница устойчивости линейной системы);

получается незатухающие колебания (рис. 16.2, а)

(16.4)

Для фазовой плоскости уравнения представляют собой параметрические уравнения эллипса с полуосями А и ωA (рис. 16.2, б).

Уравнение эллипса:

можно получить непосредственным решением дифференциального уравнения фазовых траекторий (16.3) при а₁=0 и а₂=ω², причем A — произвольная постоянная интегрирования.

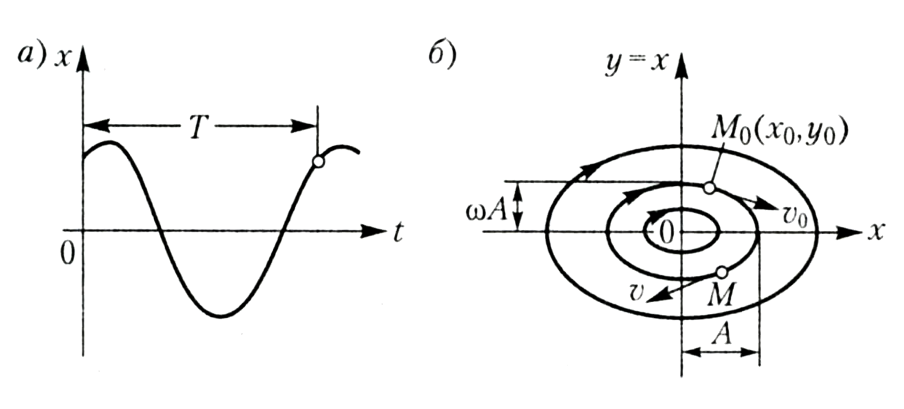
периодическим колебаниям системы (рис. 16.2, а) соответствует движение изображающей точки по замкнутой кривой (рис. 16.2, б). Фазовые траектории по замкнутой кривой

2. корни комплексные и имеют отрицательные вещественные части при (устойчивая линейная система);

это затухающие колебания (рис. 16.3, а)

Рис. 16.3

где

а произвольные постоянные A и β определяются из начальных условий:

.

Значения х и у не возвращаются за период колебания к прежним, а становятся меньше. Это дает на фазовой плоскости (х, у) кривую (рис. 16.3, б), которая за один оборот не возвращается в прежнюю точку М₀, а подходит ближе к началу координат, то есть фазовые траектории в виде спиралей(рис. 16.3, б).

3. корни комплексные и имеют положительные вещественные части при (неустойчивая линейная система);

Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траектории тоже в виде спиралей, но только изображающая точка будет двигаться по ним не к началу координат, а от него (рис. 16.4, б).

Рис. 16.4

4. корни вещественные отрицательные при (устойчивая линейная система);

апериодический процесс: (16.5)

где

Рис. 16.6

Здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка М не попадает в начало координат в конечное время, а приближается асимптотически. Фазовые траектории, вливающиеся в начало координат. (Рис. 16.6)

5. корни вещественные положительные при (неустойчивая линейная система);

Этот случай (вещественные положительные корни) соответствует также апериодическому процессу, определяемому теми же уравнениями (16.5), но при α₁<0 и α₂<0. Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные на рис. 16.6.

Рис. 16.6

6. корни вещественные и имеют разные знаки при а₂<0 (неустойчивая линейная система); в частности, один из корней будет равен нулю при а₂=0 (апериодическая граница устойчивости линейной системы).

Это апериодический процесс, но α₁ и α₂ имеют разные знаки, следовательно картина фазовых траекторий здесь иная. Так как а₂<0, то α²= –а₂, рассмотрим случай а₁=0, что соответствует согласно (16.1) уравнению системы

и согласно (16.3) — уравнению фазовых траекторий

(16.6)

Интегрирование дает

,

т.е. семейство гипербол, изображенное на рис. 16.7, б.

рис. 16.7, б.

Аналогичная картина фазовых траекторий получится в данном случае и при а₁≠0.

Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории типа рис. 16.6, б или типа рис. 16.7, б, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.