39. Основные понятия по Ляпунову об устойчивости нелинейных систем. Основные виды устойчивости нелинейных систем.

Устойчивость по Ляпунову: «Невозмущенное движение устойчиво, если при достаточно малых начальных возмущениях вызванное ими возмущенное движение сколь угодно мало отличается от невозмущенного; при этом движение асимптотически устойчиво, если при t возмущенное движение стремится к невозмущенному.»

Невозмущенным движением системы - одно из возможных расчетных движений системы при некоторых определенных начальных условиях и заданном внешнем воздействии. Всякое другое движение называется возмущенным. Можно считать, что любое возмущенное движение получается за счет приложения к системе кратковременного внешнего возмущения при t = 0.

От наличия внешних воздействий на систему, системы управления могут быть разделены на автономные и неавтономные. В автономных системах внешние воздействия отсутствуют. К автономной системе может быть сведена любая из непрерывных систем при не зависящем от времени внешнем воздействии. В неавтономных системах существуют зависящие от времени внешние воздействия.

Так как в автономных нелинейных системах наиболее характерными: являются два процесса равновесие и автоколебания, то для них рассматриваются два различных понятия устойчивости: устойчивость равновесия и устойчивость автоколебаний. Для неавтономных систем существует понятие устойчивости процесса, обусловленного внешним воздействием.

Состояние равновесия и установившийся режим автоколебаний можно рассматривать как важные частные случаи невозмущенных движений автономной системы.

Для общего суждения об устойчивости движения пользуются понятием устойчивости, данным А. М. Ляпуновым: движение устойчиво, если для любой сколь угодно малой заданной области  допустимых отклонений _k от точки _k = 0 можно указать область начальных значений лежащую внутри области и обладающую тем свойством, что ни одно возмущенное движение, начавшееся внутри области  никогда не достигнет границы области .

О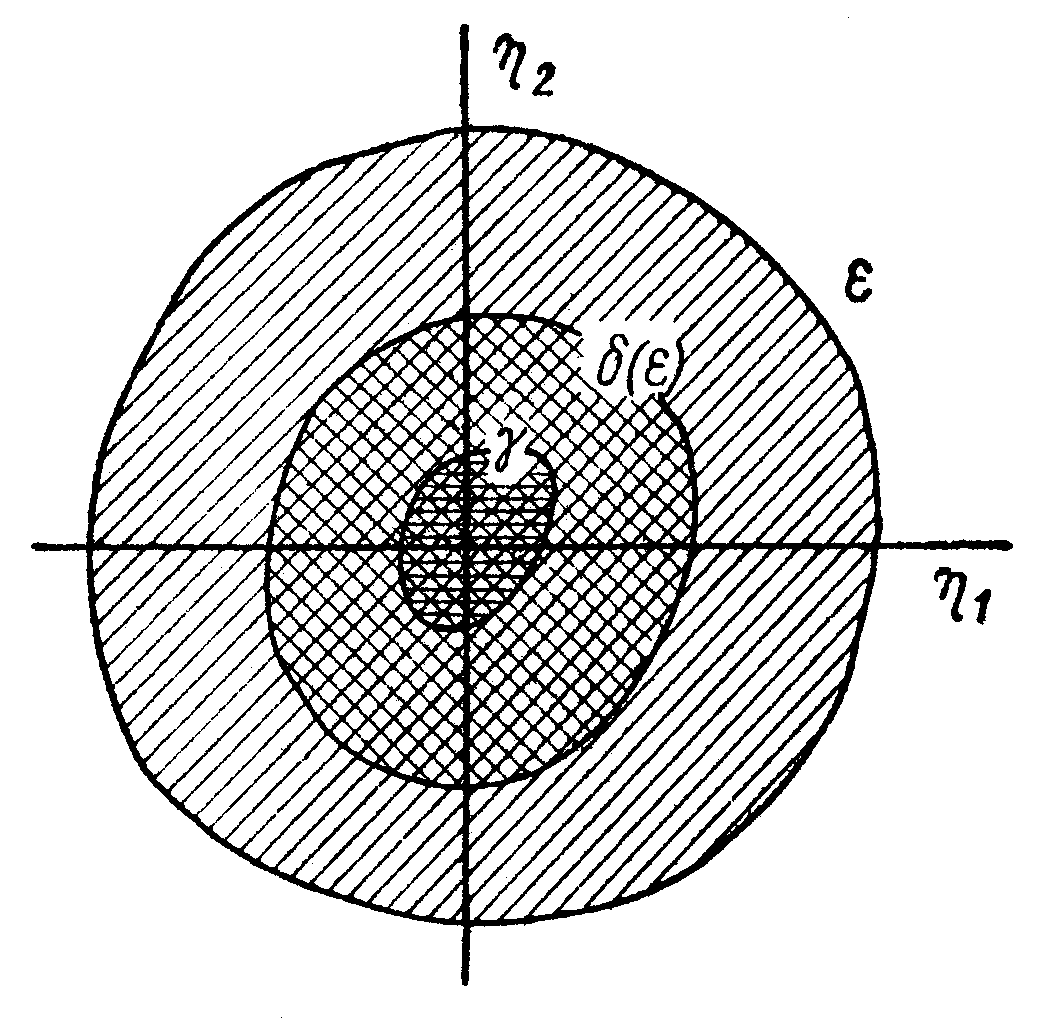бласти и  на плоскости ₁ и ₂ схематически показаны на рис. 18.1

Для характеристики устойчивости кроме областей  и  удобно ввести понятие области  установившихся значений разности возмущенного и невозмущенного движений. При t

(18.3)

Вид области  зависит от области начальных отклонений. Нужно отметить два практически важных частных случая областей . В первом случае  = 0, т. е.

(18.4)

Такое движение называют асимптотически устойчивым. Если для выполнения равенства (18.4) требуется, чтобы область начальных отклонений была достаточно мала, то говорят об асимптотической устойчивости в малом. Если эта область может иметь конечные размеры, то говорят об асимптотической устойчивости в большом. Если, наконец, равенство (18.4) выполняется при сколь угодно больших начальных отклонениях, то говорят об асимптотической устойчивости в целом.

Во втором частном случае область  представляет собой отрезок на оси ₁. В этом случае равенство (18.4) не выполняется при сколь угодно малых отклонениях от равновесия и устойчивость относится к неасимптотической.

Для суждения об устойчивости автоколебаний вводится понятие орбитальной устойчивости.

Периодическое движение (автоколебание) в пространстве состояний изображается некоторой замкнутой кривой Г. Представляя любую траекторию геометрическим местом конца вектора x(t), можно для любого момента времени t определить кратчайшее расстояние ох конца вектора x(t) до кривой Г, которое обозначим  [x(t), Г].

Под орбитально асимптотически устойчивым периодическим движением в автономной системе (автоколебанием) будем понимать такое движение, для которого

. (18.5)

Это условие можно выразить с помощью понятия невозмущенного движения, если учесть возможный сдвиг по времени  между x^H(t) и х(t).

Обозначив

, (18.6)

можно условие орбитальной асимптотической устойчивости сформулировать следующим образом: существуют такие положительные вещественные значения = ₀, для которых

(18.7)

Невыполнение условия (18.5) или (18.7) приводит к нарушению орбитальной асимптотической устойчивости.