
- •2. Функции алгебры логики
- •2.1. Элементарные функции алгебры логики
- •Теорема о замене подформул на эквивалентные
- •Некоторые свойства элементарных функций
- •2.3 Принцип двойственности
- •Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
- •Пример 3. Покажем, что функция х1х2 двойственна к x1&x2, функция х1х2 двойственна к функции x1|x2.
- •Лемма о несамодвойственной функции
- •Теорема о разложении функции по переменным
- •2.5. Полнота, примеры полных систем
- •Полные системы
- •Представление функции в виде полинома Жегалкина
- •Теорема Жегалкина
- •2.6. Замыкание и замкнутые классы
- •Важнейшие замкнутые классы в р2
- •Теорема Поста о полноте
- •Теорема о достаточности четырех функций.
- •2.7. Функции k - значной логики
- •Теорема о полной в Рk системе функций
- •4. Логика высказываний
- •4.1. Введение в логику высказываний
Теорема о полной в Рk системе функций
Cистема функций {max(x1,x2), min(x1,x2), 0, 1, ..., k–1, J0(x), J1(x), ..., Jk-1(x)} является полной в Рk и любая функция f(x1, ..., xn) Pk выражается формулой над этой системой следующим образом:
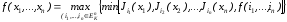 .
.
Эта формула есть своеобразный аналог СДНФ.
Доказательство.
Покажем справедливость этой формулы
на любом произвольном наборе (1,
..., n).
Слева имеем f(1,
..., n).
Справа имеем
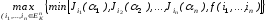 .
.
Если
для какого-нибудь j
из {1, 2, ..., n}
ij
j,
то
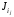 (j)
= 0 и min[J
(j)
= 0 и min[J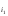 (1),
(1),
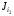 (2),
…,
(2),
…,
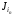 (n),
f(i1,..,in)]
= 0. Рассмотрим набор (i1,
..., in),
где i1
= 1,
i2
= ,
..., in
= n,
тогда J
(n),
f(i1,..,in)]
= 0. Рассмотрим набор (i1,
..., in),
где i1
= 1,
i2
= ,
..., in
= n,
тогда J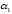 ()
= k–1,
J
()
= k–1,
J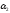 ()
= k–1,
.., J
()
= k–1,
.., J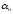 (n)
= k–1
и min[J
(n)
= k–1
и min[J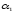 (),
... , J
(),
... , J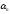 (n)
f(1,
…, n).]
= min[(k–1),
..., (k–1),
f(1,
…, n).]
= f(1,
…, n),
но тогда
(n)
f(1,
…, n).]
= min[(k–1),
..., (k–1),
f(1,
…, n).]
= f(1,
…, n),
но тогда
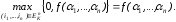 Так как набор (1,
..., n)
произвольный и равенство на нем
справедливо, то формула верна. В этой
формуле использованы функции Ji(x),
(i =
0, ..., k–1),
min(x1x2),
max(x1x2)
и константы 0, ..., k–1,
так как функция f(i1,
..., in)
есть число из {0, 1, ..., k–1}.
Так как набор (1,
..., n)
произвольный и равенство на нем
справедливо, то формула верна. В этой
формуле использованы функции Ji(x),
(i =
0, ..., k–1),
min(x1x2),
max(x1x2)
и константы 0, ..., k–1,
так как функция f(i1,
..., in)
есть число из {0, 1, ..., k–1}.
4. Логика высказываний
4.1. Введение в логику высказываний
Определение. Высказыванием называется повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.
Примеры высказываний: «2х2=4», «Волга впадает в Черное море», «Москва – столица России». Первое и третье высказывания истинны, второе – ложно. В логике высказываний простые высказывания являются булевыми переменными, принимающими значения «истина» (и) или «ложь» (л). Переменной (и) соответствует 1, переменной (л) – 0. Для них стандартным образом определяются булевы функции: дизъюнкция высказываний, конъюнкция (два последних примера), отрицание, эквивалентность, сумма по mod 2 (исключающее «или»), импликация.
Простые
высказывания (булевы переменные) будем
обозначать буквами
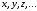 ,
если понадобится, с индексами. Булевы
функции от этих высказываний –
,
если понадобится, с индексами. Булевы
функции от этих высказываний –
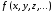 .
В логике высказываний можно ввести
стандартное для функций алгебры логики
понятие формулы. Формулы будем обозначать
буквами латинского алфавита
.
В логике высказываний можно ввести
стандартное для функций алгебры логики
понятие формулы. Формулы будем обозначать
буквами латинского алфавита
 где в скобках перечислены входящие в
формулу булевы переменные.
где в скобках перечислены входящие в
формулу булевы переменные.
Формула
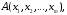 называется тавтологией,
если она принимает значение 1 для любого
набора значений входящих в нее переменных,
т.е. если она реализует функцию константа
1.
называется тавтологией,
если она принимает значение 1 для любого
набора значений входящих в нее переменных,
т.е. если она реализует функцию константа
1.
Формула
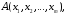 называется противоречием,
если она принимает значение 0 на всех
наборах значений переменных
называется противоречием,
если она принимает значение 0 на всех
наборах значений переменных
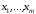 (реализует функцию константа 0).
(реализует функцию константа 0).
Формула
 называется опровержимой,
если существует набор
называется опровержимой,
если существует набор
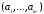 значений
значений
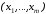 ,
такой что
,
такой что
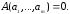
Формула
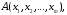 называется выполнимой,
если существует набор
называется выполнимой,
если существует набор
 значений
значений
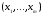 ,
такой что
,
такой что
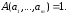
С точки зрения логики тавтология – логический закон, так как при любой подстановке вместо переменных конкретных высказываний мы получаем истинное высказывание. Перечислим наиболее важные тавтологии (А, В, С – произвольные формулы):
-
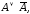 т.е.
т.е.
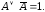 Эта тавтология называется законом
исключенного третьего или tertium
nondatur.
Эта тавтология называется законом
исключенного третьего или tertium
nondatur. -
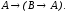
-
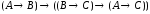 – цепное
рассуждение.
– цепное
рассуждение. -
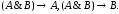
-
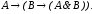
-

-
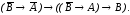
-
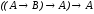 – закон Пирса.
– закон Пирса.
Любую из этих тавтологий можно обосновать, составив таблицу истинности и показав, что соответствующая функция есть константа. К этому же результату можно прийти с помощью эквивалентных преобразований.
Докажем, что
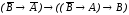 – тавтология.
– тавтология.
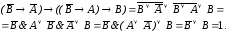
При доказательстве различных утверждений мы пользуемся «рассуждениями».
Рассуждение
называется правильным, если из конъюнкции
посылок
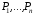 следует заключение D,
это записывается:
следует заключение D,
это записывается:
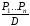 ,
т.е. всякий раз, когда все посылки истинны,
то заключение тоже истинно. Таким
образом, чтобы установить правильность
рассуждений, надо показать, что формула
,
т.е. всякий раз, когда все посылки истинны,
то заключение тоже истинно. Таким
образом, чтобы установить правильность
рассуждений, надо показать, что формула
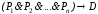 является тавтологией. Действительно,
если какая-то из посылок ложна, то
является тавтологией. Действительно,
если какая-то из посылок ложна, то
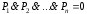 и импликация принимает значение 1. Если
все посылки истинны и рассуждения верны,
то заключение тоже должно быть верно и
импликация вновь принимает значение
1.
и импликация принимает значение 1. Если
все посылки истинны и рассуждения верны,
то заключение тоже должно быть верно и
импликация вновь принимает значение
1.
Пример
1. Рассмотрим
следующее «рассуждение»: «Если число
5 – простое, то оно нечетное. Число 5 –
нечетное, следовательно, оно простое».
Число 5 действительно простое, но сами
рассуждения неверны. Введем обозначения
для высказываний: х
– «5 – число простое», y
– «5 – число нечетное». Тогда посылками
будут
 заключением будет х. Рассуждения шли
по схеме
заключением будет х. Рассуждения шли
по схеме
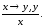 Строим формулу для определения
правильности рассуждения:
Строим формулу для определения
правильности рассуждения:
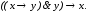 Проверим,
Проверим,
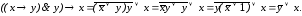
На наборе х = 0, y = 1 формула принимает значение 0, следовательно, она не является тавтологией. Эта формула будет тавтологией, если х = y, т.е. простое число и нечетное число – эквивалентные понятия. «Здравый смысл подсказывает», что в этом случае, действительно, рассуждения верны.
