2. Функции алгебры логики
2.1. Элементарные функции алгебры логики
Обозначения:
E2={0,1};
Е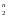
=
E2E2...E2
– прямое
произведение n
сомножителей; (x
,..,xn)
E2,
| E2|
– мощность E2,
|E2|=2,
тогда |Е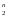
|=2n.
Определение
1. Функцией
алгебры логики называется закон,
осуществляющий отображение Е
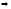E2,
причем отображение всюду определено и
функционально.
Так
как множество Е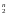
конечно,
то задать отображение Е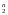
E2,
означает задать множество наборов
из Е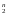
и для каждого набора указать его образ
в Е
2.
Пример
1. Пусть
n=2,
тогда Е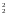
={(0
0),(0 1),(1 0),(1 1)}, отображение Е
E2
задано, например, так: (0 0) 0
; (0 1) 1;
(1 0) 1
; (1 1) 1
|
x1 x2 |
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
|
0 0 0 1 1 0 1 1 |
0 0 0 0 |
0 0 0 1 |
0 0 1 0 |
0 0 1 1 |
0 1 0 0 |
0 1 0 1 |
0 1 1 0 |
0 1 1 1 |
1 0 0 0 |
1 0 0 1 |
1 0 1 0 |
1 0 1 1 |
1 1 0 0 |
1 1 0 1 |
1 1 1 0 |
1 1 1 1 |
Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. Перечислим их.
-
f1(x1,x2) = (x1&x2), читается «конъюнкция х1 и х2», иногда вместо знака & употребляют знак
или вообще его опускают, пишут (х1х2).
(х1х2)
совпадает с обычным произведением х1х2
и совпадает с min(x1,x2).
Эту операцию называют также логическим
умножением. -
f6(x1,x2) = (x1x2) – сложение х1 и х2 по модулю два, иногда пишут (х1+х2)mod2.
3) f7(x1,x2) = (x1x2), читается «х1 дизъюнкция х2», она совпадает с max(x1,x2), ее называют логическим сложением.
4) f8(x1,x2)
= (x1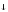
x2),
читается «х1
стрелка Пирса х2»
и совпадает с отрицанием дизъюнкции,
другие названия: функция Вебба, функция
Даггера.
5) f9(x1,x2) = (x1x2), читается «х1 эквивалентно х2».
6) f13(x1,x2)
=( x1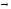
x2),
читается «х1
импликация х2»,
иногда обозначается (х1х2),
т. е. х1
влечет х2
.
7) f14(x1,x2) = (x1|x2), читается «х1 штрих Шеффера х2», она является отрицанием конъюнкции.
Рассмотрим
функции f(x1...xn),
где (x1...xn)
Е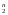
,
тогда число наборов (x1...xn),где
функция f(x1...xn)
должна быть задана, равно |Е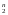
|=2n.
Обозначим множество всех функций
двузначной алгебры логики Р2.
Обозначим через Р2(n)
число функций, зависящих от n
переменных. Очевидно, Р2(n)=22
n.
Определение 3. Функция f(x1,...,xi–1,xi,xi+1,...,xn) существенно зависит от хi, если существуют такие значения 1, ...i–1, i+1, ...nпеременных x1, ...xi–1, xi+1, ...xn, что f(1, ...i–1 i+1.n)f(1...i–1 i+1.n) . Тогда переменная хi называется существенной переменной. В противном случае хi называется фиктивной переменной.
Определение 1. Пусть МP2, тогда:
1) каждая функция f(x1, ..., xn) называется формулой над ;
2) пусть g(x1, ..., xm)G1, ..., Gm – либо переменные, либо формулы над . Тогда выражение g(G1...Gn) – формула над .
Формулы будем обозначать заглавными буквами: N[f1, ..., fs], имея в виду функции, участвовавшие в построении формулы, или N(х1, ..., xk) имея в виду переменные, вошедшие в формулу. Gi – формулы, участвовавшие в построении g(G1, ..., Gn), называются подформулами.
Пример 1. Пусть N={(x1x2),(x1x2),(x )}, тогда ((х1х2)х3) – формула над .
Сопоставим каждой формуле N(x1, ..., xn) функцию f(x1, ..., xn)P2. Сопоставление будем производить в соответствии с индуктивным определением формулы.
1) Пусть N(x1, ..., xn)=f(x1, ..., xn), тогда формуле N(x1, ..., xn) сопоставим функцию f(x1, ..., xn).
2)
Пусть N(x1,
..., xn)=g(G1,
..., Gm),
где каждое Gi
– либо
формула над M,
либо переменная, тогда по индуктивному
предположению каждому Gi
сопоставлена
либо функция fiP2
, либо переменная хi
, которую
можно считать тождественной функцией.
Таким образом, каждой формуле Gi
сопоставлена функция fi(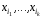
),
причем:{
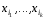}{x1,
..., xn},
т.к. в формуле N(x1,
..., xn)
перечислены все переменные, участвовавшие
в построении формулы. Можно считать,
что все функции fi
зависят от переменных (x1,
..., xn),
причем какие-то переменные могут быть
фиктивными. Тогда N(x1,
..., xn)
= g(G1,
..., Gm)
= g(
f1(x1,
..., xn),
..., fm(x1,..,xn)).
Сопоставим этой формуле функцию h(x1,
..., xn)
следующим образом: пусть (1,
..., n)
– произвольный набор переменных (x1,
..., xn).
Вычислим значение каждой функции fi
на этом наборе, пусть f(1,
..., n)=i,
затем найдем значение функции g(x1,
..., xm)
на наборе (1,
..., m)
и положим h(1,
..., n)
= g(1,
..., m)
= g(f1(1,
..., n),
..., fm(1,
..., n)).
Так как каждое fi(x1,
..., xn)
есть функция, то на любом наборе (1,
..., n)
она определяется однозначно, g(x1,
..., xm)
– тоже функция, следовательно, на наборе
(1,
..., n)
она определяется однозначно, где h(x1,
..., xn)
есть функция, определенная на любом
наборе (1,
..., n).
Множество всех формул над M обозначим через <M>.