
- •2. Функции алгебры логики
- •2.1. Элементарные функции алгебры логики
- •Теорема о замене подформул на эквивалентные
- •Некоторые свойства элементарных функций
- •2.3 Принцип двойственности
- •Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
- •Пример 3. Покажем, что функция х1х2 двойственна к x1&x2, функция х1х2 двойственна к функции x1|x2.
- •Лемма о несамодвойственной функции
- •Теорема о разложении функции по переменным
- •2.5. Полнота, примеры полных систем
- •Полные системы
- •Представление функции в виде полинома Жегалкина
- •Теорема Жегалкина
- •2.6. Замыкание и замкнутые классы
- •Важнейшие замкнутые классы в р2
- •Теорема Поста о полноте
- •Теорема о достаточности четырех функций.
- •2.7. Функции k - значной логики
- •Теорема о полной в Рk системе функций
- •4. Логика высказываний
- •4.1. Введение в логику высказываний
Теорема о замене подформул на эквивалентные
Пусть N<M> и имеет вид: N(x1, ..., xn) = g(G1, ...Gi, ...,Gm). Пусть подформула Gi~Gi, тогда формула N(x1, ..., xn) = g(G1, ...,Gi,...,Gm) эквивалентна формуле N(x1, ..., xn) = g(G1, ..., Gi, ...,Gm).
Доказательство. Формулы N и N эквивалентны, если реализуют одну и ту же функцию. Согласно построению функции, реализующей формулу имеем:
N(x1, ..., xn) = g(f1(x1, ..., xn ), ..., fi(x1, ..., xn), ..., fm(x1, ..., xn)),
N (x1, ..., xn)= g(f1 (x1, ..., xn ), ..., fi(x1, ..., xn), ..., fm (x1, ..., xn)).
По условию Gi~Gi, следовательно на наборе 1, ..., n) имеем fi 1, ..., n) = = fi1, ..., n) следовательно, на любом наборе 1, ..., n)значения функции g(f1, ...,fi, ...,fm) и g(f1, ...,fi, ...,fm) совпадают. Получим N~N.
Некоторые свойства элементарных функций
1. Идемпотентность & и : х&x=x , xx=x.
2. Коммутативность
&,,,|,~,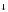 .
.
3. Ассоциативность &,,,~, поэтому в формулах вида xyz можно не ставить никаких скобок.
4. Дистрибутивность:
а) & по отношению к : x&(yz)=xyxz ,
б) по отношению к &: x(y&z)=(xy)&(xz) ,
в) & по отношению к : x(yz)=xyxz .
5. Инволюция :
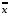 =х
.
=х
.
6. Правило де
Моргана: 
 =
=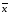 &
& и
и
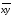 =
=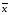
 .
.
7. Законы действия с 0 и 1:
x0=x
, x1=1
, x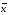 =1
, x&0=0
, x&1=x
, x&
=1
, x&0=0
, x&1=x
, x& =0
, x1=
=0
, x1=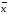 , x0=x.
, x0=x.
8.
Самодистрибутивность импликации:
x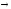 (y
(y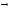 z)=(x
z)=(x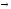 y)
y)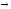 (x
(x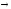 z).
z).
Равенство всех этих формул доказывается по определению, т.е. по равенству функций, которые они реализуют.
Проверим
для примера самодистрибутивность
импликации : x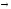 (y
(y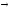 z)=(x
z)=(x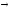 y)
y)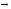 (x
(x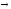 z).
z).
|
x |
y |
z |
y |
x |
x |
x |
|
|
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
1 1 0 1 1 1 0 1 |
1 1 1 1 1 1 0 1 |
1 1 1 1 0 0 1 1 |
1 1 1 1 0 1 0 1 |
1 1 1 1 1 1 0 1 |
2.3 Принцип двойственности
Определение
1.
Функции f*(x1,
..., xn)
называется двойственной к функции f(x1,
..., xn),
если f*(x1,
..., xn)
=
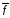 (
(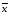 1,
...,
1,
...,
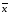 n).
n).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
|
x |
f |
f* |
|
0 1 |
0 0 |
1 1 |
Функции
f(x)
= x
и g(x)
=
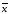 двойственны сами себе:
двойственны сами себе:
|
x |
f |
f* |
g |
g* |
|
0 1 |
0 1 |
0 1 |
1 0 |
1 0 |
так
как f*(0)=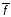 (1).
(1).
Определение 2. Если f*(x1, ..., xn) = f(x1, ..., xn), то f(x1, ..., xn) называется самодвойственной.
Пример 2. Покажем, что f(x1,x2,x3)=x1x2x3 – самодвойственна:
|
x1 |
x2 |
x3 |
f |
f* |
|
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 1 1 0 1 0 0 1 |
0 1 1 0 1 0 0 1 |
Если
f*–
самодвойственна, то
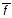 (
(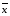 1,
...,
1,
...,
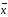 n)
= f(x1,
..., xn),
т.е. на противоположных наборах функция
принимает противоположные значения.
n)
= f(x1,
..., xn),
т.е. на противоположных наборах функция
принимает противоположные значения.

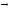 z
z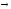 (y
(y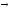 z)
z) y
y z
z