7.2. Классификация зубчатых механизмов

Зубчатые механизмы классифицируются:

а) по виду расположения осей – различают зубчатые механизмы:

• цилиндрические – при передаче вращения между параллельными осями (рис. 67);

^{а) б) в) г)}

Рис. 67. Цилиндрические зубчатые механизмы

• конические – при передаче вращения между пересекающимися осями (рис. 68);

Рис. 68. Конические зубчатые механизмы

• винтовые – при передаче вращения между скрещивающимися осями (рис. 69).

Рис. 69. Винтовой зубчатый механизм

б) по виду зацепления – зубчатый механизм может быть с зацеплением зубьев:

• внешним (рис. 67, а);

• внутренним (рис. 67, г);

• реечным (рис. 67, в).

в) по расположению зубьев колес относительно образующей обода – различают зубчатые передачи:

• прямозубые (рис. 67, а);

• косозубые (рис. 67, б).

7.3. Основная теорема зацепления

Общая нормаль к соприкасающимся профилям зубьев в данный момент зацепления делит линию центров колес на части, обратно пропорциональные угловым скоростям.

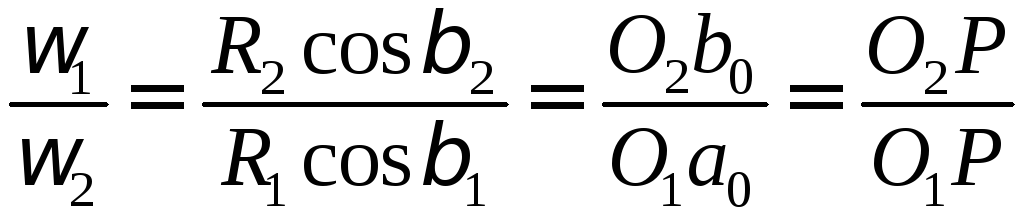
Следствие 1. Проекции скоростей на общую касательную не равны между собой. Поэтому зацепление зубьев происходит со скольжением профилей, от которого возникает износ и потери на трение, зависящие от скорости скольжения .

Скольжения не будет только тогда, когда , т. е. в момент зацепления зубьев на линии центров.

Следствие 2. Для постоянства передаточного отношения необходимо, чтобы общая нормаль NN в любой момент зацепления проходила через одну и ту же точку на линии центров, называемую полюсом зацепления Р.

Окружности, проходящие через полюс зацепления, называют начальными (r_ω1 и r_ω2).

Расстояние по дуге начальной окружности между двумя соседними зубьями называется шагом по начальной окружности (P_ω1 и P_ω2). Так как начальные окружности – центроиды, то P_ω1 = P_ω2 = P_ω.

Числа зубьев колес обычно обозначаются через z (z₁ и z₂). Тогда следующие равенства очевидны: и .

Из основной теоремы зацепления для круглых колес имеем:

, (7.1)

т. е. передаточное отношение пары зубчатых колес с неподвижными осями обратно пропорционально числу зубьев, взятому с соответствующим знаком. Для внешнего зацепления – знак «минус», для внутреннего – «плюс».

В настоящее время в машиностроении и приборостроении основной кривой для профилей зубьев является эвольвента круга, предложенная Л. Эйлером в 1754 г.

7.4. Эвольвента и её свойства

Эвольвента представляет собой развертку круга (рис. 71, а).

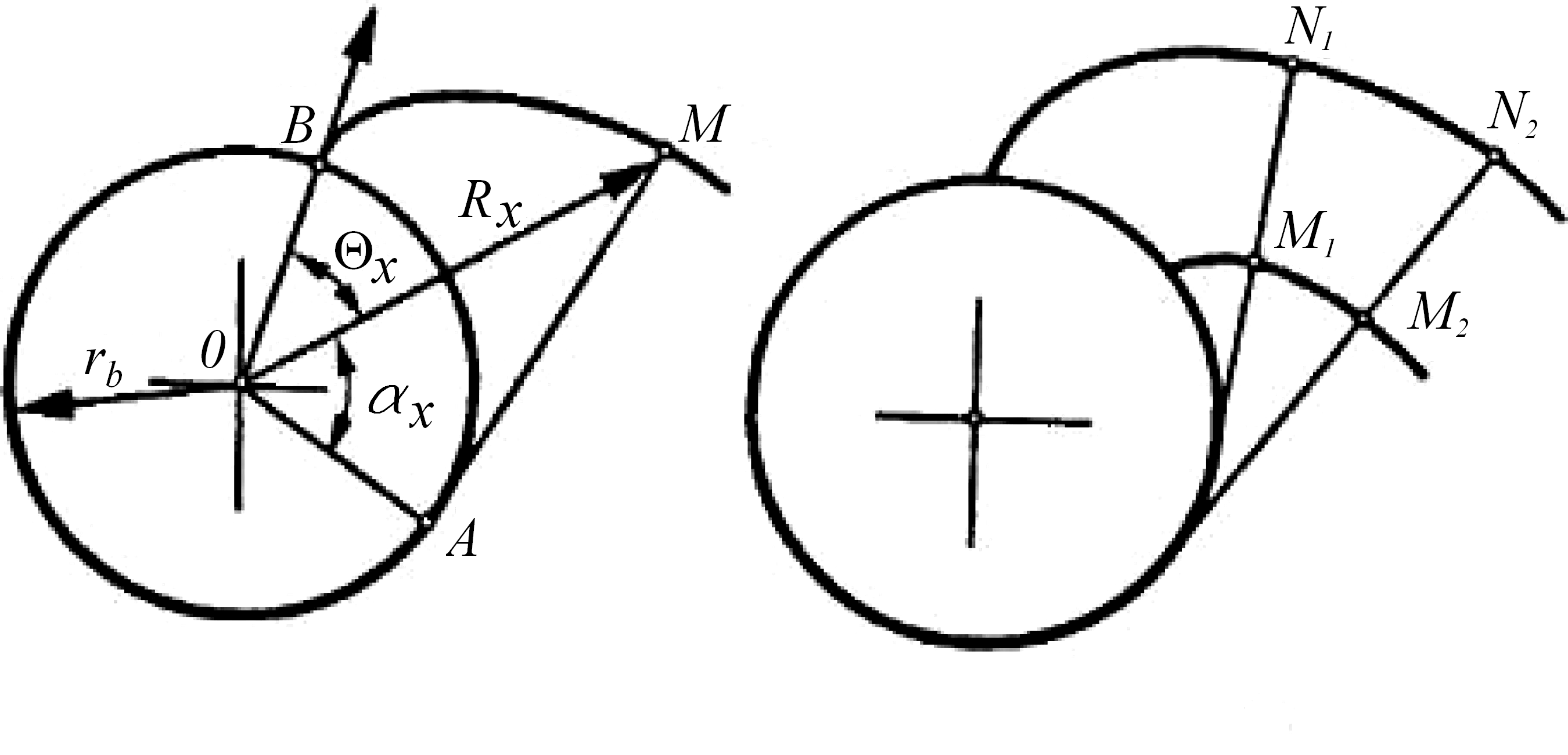
Рис. 71. Образование эвольвенты

Развертываемую окружность (эволюту) принято в теории зубчатых колес называть основной окружностью радиуса r_b. Из способа образования эвольвенты следует, что всегда АВ = AM, т. е.:

.

Отсюда: , а из :

. (7.3)

Это уравнение является параметрическим уравнением эвольвенты в полярных координатах. Полярная ось при этом проходит через начало эвольвенты (точка В). Угол – центральный угол между полярной осью и радиус-вектором в точку М. Разность () часто встречается в теории зубчатых колес и для упрощения расчетов представлена в справочных таблицах под названием «Инволюта угла »:

.

Следующие свойства эвольвенты, используемые в зубчатых колесах, очевидны:

• нормаль к эвольвенте является касательной к основной окружности;

• радиус кривизны эвольвенты в любой ее точке равен расстоянию от эвольвенты до точки касания нормали с основной окружностью, т. е. РM = AM;

• две эвольвенты одной окружности эквидистантны, т. е. равно отстоят друг от друга (M₁N₁ = M₂N₂) (рис. 71, б).

Определение эвольвенты и ее аналитическое уравнение используются также для графического построения эвольвенты.