8.6. Планы линейных и угловых скоростей планетарных механизмов

Планы линейных и угловых скоростей планетарных механизмов дают наглядное представление о распределении скоростей по звеньям. Они позволяют легко определить скорости в относительном и абсолютном движении, необходимые для прочностного и динамического расчетов (учет динамики зацепления, КПД и т. п.).

Построение плана линейных скоростей основано на теореме о распределении скоростей по твердому телу и свойствах начальных окружностей (качении без скольжения).

Рассмотрим построение на примере AJ-механизма (рис. 99).

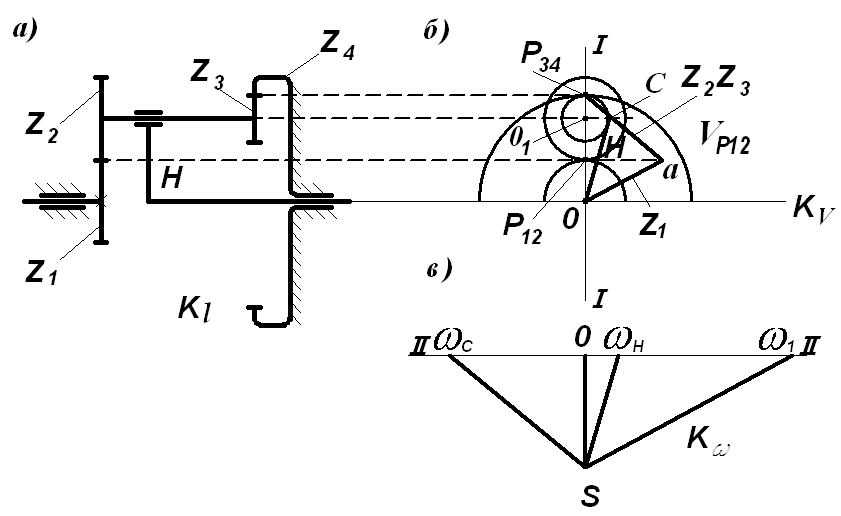
Рис. 99. Построение планов скоростей и ускорений планетарного механизма

Выбирается прямая I–I, представляющая собой линию центров второй проекции схемы механизма. При известной угловой скорости звена z₁ можно определить скорость на начальной окружности r₁ как V_P12 = r₁= k_v. Точка О на оси имеет нулевую скорость. Знание скоростей двух точек позволяет построить прямую Оа, представляющую собой закон распределения скоростей по z₁. Для сателлита z₂-z₃ известны скорость в точке Р₁₂ и скорость в полюсе Р₃₄ (равная нулю, так как z₄ неподвижно). Распределение скоростей по сателлиту выражается прямой Р₃₄а.

На оси сателлита V₀₁ = k_v и, следовательно, прямая ОС выражает распределение скоростей по водилу.

Так как угловая скорость , т. е. на графике пропорциональна тангенсу угла наклона прямой распределения скоростей, то, проведя из произвольной точки S прямые, параллельные линиям распределения линейных скоростей, получим на прямой II–II от точки О отрезки, дающие абсолютные угловые скорости в масштабе:

. (8.21)

36