1.4. Приведение подобных слагаемых

Задание 5. Привести подобные слагаемые полинома с помощью меню, выполнив следующие операции:

1. Введите текстовую область Задание 5.

2. Введите выражение .

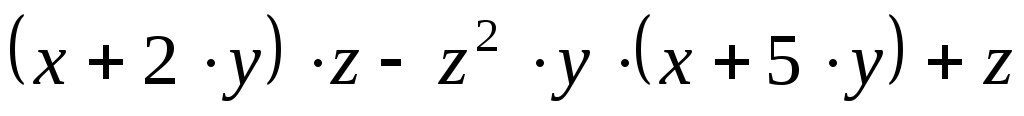3. Выделите в выражении имя переменной, относительно которой надо привести подобные слагаемые (например, по y).

4. Выберите команду Symbolics, Collect (Символы, Подобные). На экране появится выражение: .

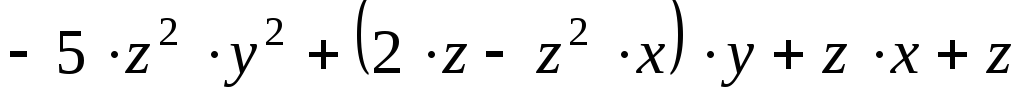5. Самостоятельно приведите подобные относительно переменной x.

6. Повторно введите исходное выражение и приведите подобные, используя оператор collect палитры Symbolic (Символы). В местозаполнитель этого оператора можно вставлять несколько переменных через запятую (например; x,y,z).В этом случае приведение подобных слагаемых выполняется последовательно по всем переменным. Должен получиться следующий результат: .

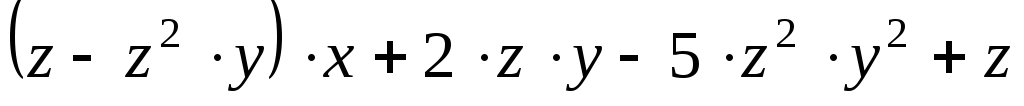7. Сохраните изменения в текущем документе.

1.5. Определение коэффициентов полинома (Polynomial Coefficients)

Если выражение является некоторым полиномом относительно переменной x, заданным не в обычном виде , а как произведение других, более простых полиномов, то коэффициенты легко определяются символьным процессором MathCAD. Коэффициенты сами могут быть функциями других переменных.

Задание 6. Вычислить полиномиальные коэффициенты в выражении: .

Порядок выполнения задания:

1. Введите текстовую область Задание 6.

2. Введите выражение и выделите в нем переменную z.

3. Выполните команду Symbolic, Polynomial Coefficients (Символы, Коэффициенты полинома). Результат будет выдан в виде вектора

.

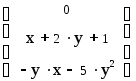Первый элемент вектора является свободным членом а₀, второй – а₁, и т.д.

4. Повторно введите исходное выражение и вычислите коэффициенты полинома относительно переменной x с использованием оператора символьного вывода coeffs палитры Symbolic. Процесс должен выглядеть так:

.

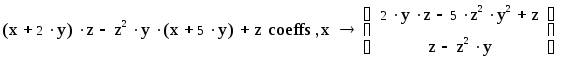5. Сохраните изменения в текущем документе.

MathCAD дает возможность определения коэффициентов не только для отдельных переменных, но и для сложных выражений, входящих в формулу в качестве составной части. Например:

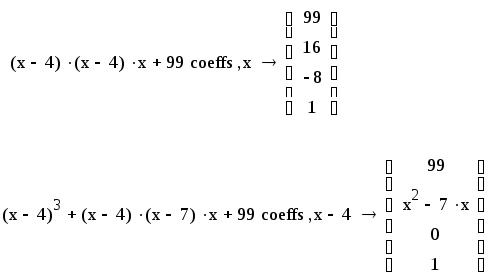
Введите эти выражение и получите результаты самостоятельно.

1.6. Разложение на элементарные дроби

Чтобы разложить сложную дробь на более простые дроби, следует выполнить команду Symbolics, Variable, Convert to Partial Fractions (Символы, Переменные, Преобразование в Частичные доли).

Задание 7. Разложить на элементарные дроби следующее выражение

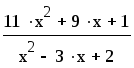
Порядок выполнения задания:

1. Введите текстовую область Задание 7.

2. Введите исходное выражение и выделите в нем переменную x.

3. Используя меню, подайте команду на выполнение операции разложения. На экран будет выведен результат:

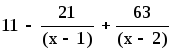
4. Повторите операцию разложения, используя команду convert палитры Symbolic.

5. Сохраните изменения в текущем документе.

1.7. Подстановка переменной (Substitute)

Очень удобная возможность символьных вычислений – это операция подстановки значения переменной в выражение. Значение переменной может быть любым выражением относительно любых переменных.

Задание 8. Подставить значение a·x² вместо переменной y в выражение sin(k·y²+b·y).

Порядок выполнения задания:

1. Введите текстовую область Задание 8.

2. Введите значение переменной a·x² и скопируйте его в буфер.

3. Введите выражение sin(k·y²+b·y) и выделите в выражении переменную, вместо которой следует поставить значение из буфера (переменную y).

4. Подайте команду Symbolics, Variable, Substitute (Символы, Переменные, Замена). Результат будет выглядеть так: