2.3. Метод половинного деления

Среди численных методов решения уравнения (2.1) наиболее простым в реализации является метод половинного деления. Он позволяет отыскивать корень уравнения (2.1) с любой заданной точностью и применим в том случае, если – непрерывна на и . Суть метода состоит в следующем.

Разбиваем пополам; среди двух получившихся отрезков выбираем тот, на концах которого принимает значения разных знаков. Получаем новый отрезок , внутри которого находится точный корень уравнения. Данный процесс деления и выбора нового более узкого отрезка продолжаем до тех пор, пока на n-ом шаге длина полученного отрезка не станет меньше . Тогда приближенный корень уравнения может быть найден по формуле

(2.3)

При этом абсолютная погрешность найденного корня не превышает , т. е. . Может случиться, что на некотором шаге значение в середине отрезка равно нулю. Тогда середина отрезка – точный корень уравнения (3.1).

2.4. Метод Ньютона

Пусть корень уравнения (2.1) отделен на начальном отрезке , причем и и отличны от нуля и знакопостоянны на этом отрезке. Ограничения на производные геометрически означают, что кривая не только идет в одном направлении, – все время вверх или все время вниз , но к тому же строго выпукла вниз или вверх .

Геометрический смысл метода Ньютона или иначе – метода касательных состоит в том, что к графику функции проводится касательная в некоторой точке с абсциссой , и вместо точки пересечения графика с осью Ox ищется точка пересечения этой касательной с осью Ox (рис. 2.3).

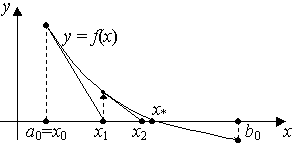
Рис. 2.3. Геометрическая иллюстрация метода Ньютона

В качестве начальной точки выбирается тот из концов отрезка , в котором функция и ее вторая производная имеют один и тот же знак

(2.4)

Затем строят касательную к графику в точке с абсциссой , находят абсциссу точки пересечения касательной с осью Ox. Снова строят касательную к графику уже в точке и находят абсциссу точки пересечения новой касательной с осью Ox. Продолжая этот процесс, получают числовую последовательность

(2.5)

Можно доказать [2], что при выполнении перечисленных в начале этого параг-рафа условий, последовательность (2.5) сходится к корню уравнения (2.1).

Получим расчетную формулу для метода Ньютона. Пусть и – предыдущее и последующее приближения корня. Запишем уравнение касательной к графику функции в точке : . В уравнении положим , тогда (так как это точка пересечения касательной с осью Ox). Значит . Разрешая это уравнение относительно , находим

(2.6)

Полученная рекуррентная формула (2.6) определяет сходящуюся к числовую последовательность. Погрешность приближенного к значения определяется из неравенства, установленного в работах [2], [3]:

(2.7)

где

2.5. Метод хорд

Пусть корень уравнения (2.1) отделен на начальном отрезке , причем и существуют и знакопостоянны и для всех . Геометрический смысл метода хорд состоит в том, что к графику функции на отрезке, внутри которого находится корень, проводится стягивающая его хорда и вместо точки пересечения графика с осью Ox ищется уже точка пересечения этой хорды с осью Ox. В качестве начального приближения к корню выбирается тот из концов отрезка , в котором функция и ее вторая производная имеют противоположные знаки, т. е.

(2.8)

При этом противоположный конец отрезка будет неподвижен. Этот неподвижный конец отрезка обозначим через C (рис. 2.4). Строя последовательно указанным выше способом хорды и находя их точки пересечения с осью Ox, получаем последовательность приближений искомого корня

,

которая при выполнении отмеченных в начале параграфа условий, будет сходиться к корню уравнения (2.1).

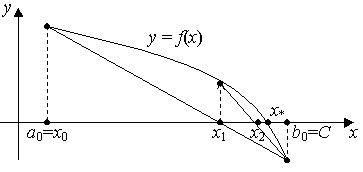
Рис. 2.4. Геометрическая иллюстрация метода хорд

Получим расчетную формулу для метода хорд. Пусть и – предыдущее и последующее приближения корня, C – неподвижная точка. Запишем уравнение прямой (хорды), проходящей через две точки с координатами и . Получим

.

В уравнении положим , тогда и уравнение примет вид

.

Разрешая это уравнение относительно , получим рекуррентную формулу для последовательности приближений корня уравнения (2.1)

(2.9)

При этом погрешность приближения на n-ом шаге определяется следующим неравенством [2], [3]:

(2.10)

где