3.7. Порядок выполнения работы в компьютерном классе
1. Прежде чем начать выполнение лабораторной работы на ЭВМ, внимательно ознакомьтесь с данной инструкцией.
2. При
необходимости включите сами (или
попросите лаборанта) питание компьютера.
После того, как система загрузится,
запускаем двойным щелчком левой кнопки
мыши на рабочем столе программу Mathcad,
если же ярлык отсутствует, тогда открываем
программу через кнопку «Пуск» (Программы
Mathsoft
Mathcad).
3. Узнайте
у лаборанта расположение пакета Lab
и откройте файл Lab3.mcd
(File
Open или, если программа
русифицирована, Файл
Открыть). При любой ошибке ввода программы
нужно обратиться к лаборанту.
4. Прочитайте в начале файла задание на лабораторную работу и просмотрите пример выполнения работы, для которого исследование уже проведено. В файле Lab3.mcd в разделе «Основные численные методы интегрирования» запрограммированы в соответствующих пунктах методы правых прямоугольников, левых прямоугольников, средних прямоугольников, трапеций и Симпсона. В конце соответствующих пунктов заложены формулы (3.23)-(3.26), позволяющие определить число точек разбиения отрезка интегрирования, обеспечивающее любую заданную точность. В последнем разделе «Вычисление неопределенных интегралов. Формула Ньютона- Лейбница» приведены дополнительные сведения о возможностях системы Mathcad по нахождению неопределенных интегралов в конечном аналитическом виде через элементарные функции и применению формулы Ньютона-Лейбница для нахождения точных значений определенного интеграла.
5. Введите
вместо задания примера свои данные
.
При вводе числовых данных, являющихся
десятичными дробями, целую и дробную
части нужно разделять точкой (например,
0.8, 1.2 и т. д.). Для набора необходимой Вам
функции
нужно либо скопировать ее из варианта,
приведенного в конце файла, либо
воспользоваться всплывающим меню
инструментов «Calculator»,
либо ввести ее с клавиатуры, используя
следующие символы арифметических
действий и стандартных функций: сложение
– ‘+’; вычитание – ‘–‘; умножение –
‘*’; деление – ‘/’; возведение в степень
– ‘^’; квадратный корень – ‘\’; модуль
– ‘|’; число
– ‘Ctrl’+‘Shift’+‘P’;
число
– ‘e’; синус – sin(x);
косинус – cos(x);
тангенс – tan(x);
котангенс – cot(x);
арксинус – asin(x);
арккосинус – acos(x);
арктангенс – atan(x);
арккотангенс – acot(x);
экспонента – exp(x);
натуральный логарифм – ln(x).
6. Дальнейший порядок выполнения работы Вам укажет программа подсказками и заданиями, выделенными красным цветом.
3.6. Пример выполнения работы
Вычислить
интеграл:
.
1.
Разобьем отрезок интегрирования
на 8 частей. В результате
получим, что шаг интегрирования
,
а точки разбиения:
Вычислим
значения функции
и конечные разности
по формулам (3.17) в этих точках. Результаты
занесем в табл. 3.2.
Таблица 3.2
Результаты вычислений
и конечных разностей
|
I |
|
|
|
|
|
|
|
0 |
8.0 |
0,199218 |
– 0,032152 |
0,005024 |
– 0,000718 |
0,000073 |
|
1 |
8.9 |
0,167066 |
– 0,027128 |
0,004306 |
– 0,000641 |
0,000075 |
|
2 |
9,8 |
0,139938 |
– 0,022822 |
0,003665 |
– 0,000566 |
0,000079 |
|
3 |
10,7 |
0,117116 |
– 0,019157 |
0,003099 |
– 0,000487 |
0,000069 |
|
4 |
11,6 |
0,097959 |
– 0,016058 |
0,002613 |
– 0,000418 |
0,000065 |
|
5 |
12,5 |
0,081901 |
– 0,013445 |
0,002195 |
– 0,000353 |
|
|
6 |
13,4 |
0,068456 |
– 0,011250 |
0,001842 |
|
|
|
7 |
14,3 |
0,057206 |
– 0,009408 |
|
|
|
|
8 |
15,2 |
0,047798 |
|
|
|
|
2. По формуле трапеций (3.4) находим
3. Аналогично проводим вычисления по формуле Симпсона (3.9):
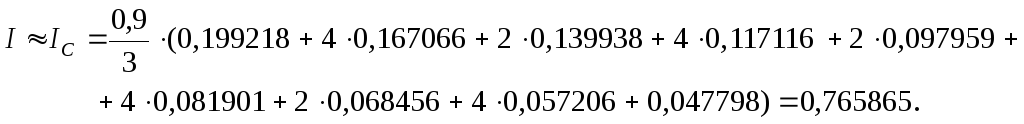
4. Оценим погрешности вычислений. Погрешность округления
(значения
функции
вычислены с ошибкой
,
так как округления производились в
шестом знаке после запятой). Оценку
погрешностей методов проводим по
формулам (3.21) и (3.22). Так как
,
то для метода трапеций
и полная
погрешность
Следовательно
.
Соответственно для метода Симпсона
имеем
и
Поэтому
Таким образом, метод Симпсона дает
значительно более точный результат,
чем метод трапеций.
5. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab3.mcd. Вводим функцию
,
а также нижний и верхний предел интегрирования
Программа
автоматически строит график подынтегральной
функции
на отрезке
(рис. 3.7).
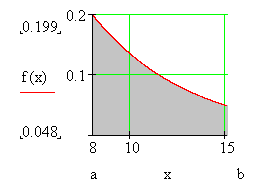
Рис. 3.7. График подынтегральной функции
Таким образом, из геометрического смысла определенного интеграла следует, что необходимо вычислить площадь криволинейной трапеции (серая область на рис. 3.7).
Программа
автоматически вычисляет интеграл с
точностью до
:
6. Выписываем полученное на компьютере решение
и вычисляем абсолютные погрешности, с какими найдены с помощью МК значения интеграла по методу трапеций и Симпсона:
7.
Используя формулы (3.23), программа в конце
пункта «Метод левых прямоугольников»
вычислит число точек разбиения отрезка
интегрирования
,
обеспечивающее точность
методов левых и правых прямоугольников.
Получим
.
Подставляя
в начало пункта «Метод правых
прямоугольников» программы, выписываем
получившееся решение
с абсолютными погрешностями
8.
Используя формулу (3.24), программа в конце
пункта «Метод средних прямоугольников»
вычисляет число точек разбиения отрезка
интегрирования
,
обеспечивающее точность
метода средних прямоугольников. Получим
.
Подставляя
в начало пункта «Метод средних
прямоугольников» программы, выписываем
получившееся решение
с абсолютной погрешностью
9.
Используя формулу (3.25), программа в конце
пункта «Метод трапеций» вычисляет число
точек разбиения отрезка интегрирования
,
обеспечивающее точность
метода трапеций. Получим
.
Подставляя
в начало пункта «Метод трапеций»
программы, выписываем получившееся
решение
с абсолютной погрешностью
10.
Используя формулу (3.26), программа в конце
пункта «Метод Симпсона» вычисляет число
точек разбиения отрезка интегрирования
,
обеспечивающее точность
метода Симпсона. Получим
.
Следовательно, так как n
должно быть четным, подставляем
в начало пункта «Метод Симпсона»
программы. Выписываем получившееся
решение
с абсолютной погрешностью
11. Все расчеты оформляются в виде отчета по лабораторной работе.