4.6. Порядок выполнения работы в компьютерном классе

1. Прежде чем начать выполнение лабораторной работы на ЭВМ, внимательно ознакомьтесь с данной инструкцией.

2. При необходимости включите сами (или попросите лаборанта) питание компьютера. После того, как система загрузится, запускаем на рабочем столе программу Mathcad, если же ярлык отсутствует, тогда открываем программу через кнопку «Пуск» (Программы Mathsoft Mathcad).

3. Узнайте у лаборанта расположение пакета Lab и откройте файл Lab4.mcd (File Open или если программа русифицирована Файл Открыть). При любой ошибке ввода программы нужно обратиться к лаборанту.

4. Прочитайте в начале файла задание на лабораторную работу и просмотрите пример выполнения работы, для которого исследование уже проведено. В файле Lab4.mcd в разделе «Решение задачи Коши с помощью встроенной функции системы Mathcad» для нахождения решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производной, используется метод Рунге-Кутта, заложенный в программный блок «Given – – odesolve(x,b,[step])», где x – переменная интегрирования, b – конечная точка интегрирования, [step] – шаг интегрирования (по умолчанию равен 0.1). Во втором разделе «Метод Эйлера» и третьем разделе «Метод Рунге-Кутта» запрограммированы одноименные методы, с помощью которых можно проверить полученные на МК приближенные решения, и построены графики точного решения и интегральных кривых, полученных этими методами.

5. Далее введите вместо задания примера, свои данные . При вводе числовых данных, являющихся десятичными дробями, целую и дробную части нужно разделять точкой (например, 3.2, 1.6 и т. д.). Для набора необходимой Вам функции нужно либо скопировать ее из варианта, приведенного в конце файла, либо воспользоваться всплывающим меню инструментов «Calculator», либо ввести ее с клавиатуры, используя следующие символы арифметических действий и стандартных функций: сложение – ‘+’; вычитание – ‘–‘; умножение – ‘*’; деление – ‘/’; возведение в степень – ‘^’; квадратный корень – ‘\’; модуль – ‘|’; число – ‘Ctrl’+‘Shift’+‘P’; число – ‘e’; синус – sin(x); косинус – cos(x); тангенс – tan(x); котангенс – cot(x); арксинус – asin(x); арккосинус – acos(x); арктангенс – atan(x); арккотангенс – acot(x); экспонента – exp(x); натуральный логарифм – ln(x).

6. Дальнейший порядок выполнения работы Вам укажет программа подсказками, указаниями и заданиями, выделенными красным цветом.

4.7. Пример выполнения работы

Решить задачу Коши:

1. Решаем задачу методом Эйлера на микрокалькуляторе. В нашем случае a=2, b=3,6, поэтому шаг интегрирования будет равен

Записываем формулу (4.3) для нашей задачи

Выполняя последовательно по этой формуле расчеты с шагом и с шагом , заполняем табл. 4.2.

Таблица 4.2

Решение задачи Коши методом Эйлера

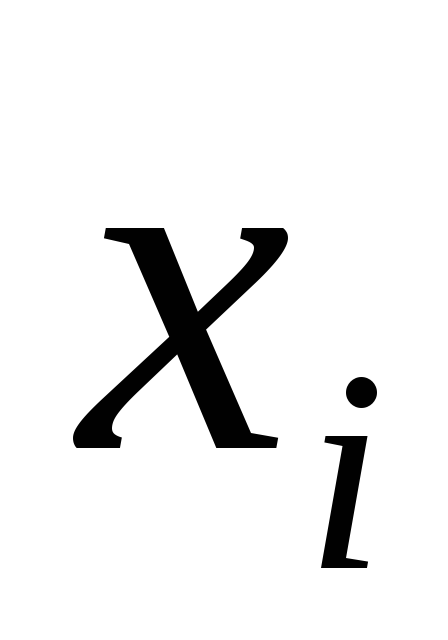
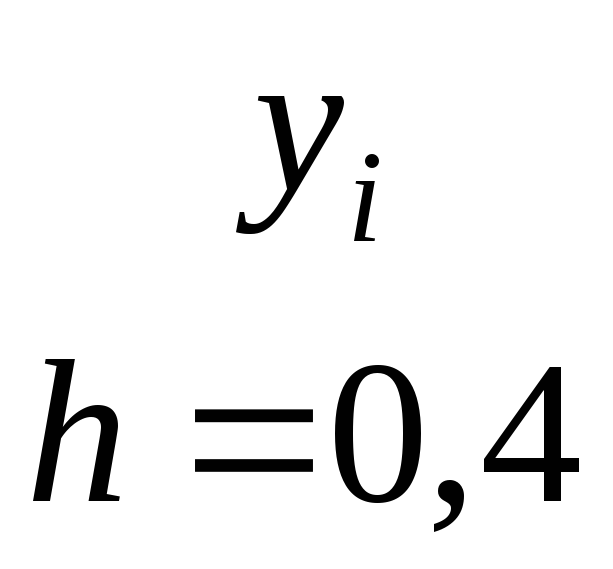
2,0	1,000	1,000	0,000
2,2	1,119
2,4	1,260	1,238	0,022
2,6	1,428
2,8	1,626	1,567	0,059
3,0	1,860
3,2	2,135	2,015	0,120
3,4	2,460
3,6	2,843	2,626	0,217

Находим максимум величин , определяем, что локальная погрешность решения, полученного с шагом , не превышает 0,217.

2. Решаем задачу методом Рунге-Кутта на микрокалькуляторе. В нашем случае a=2, b=3,6, поэтому шаг интегрирования будет равен

Записываем формулы (4.5), (4.6) для нашей задачи

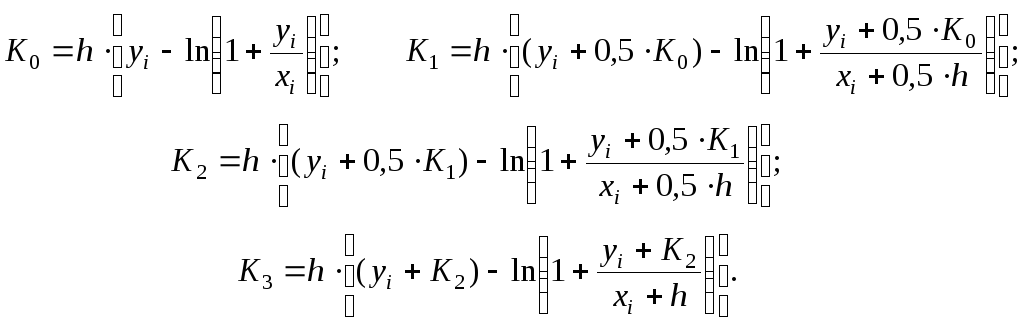
Выполняя последовательно по этим формулам расчеты с шагом , заполняем табл. 4.3.

Таблица 4.3

Решение задачи Коши методом Рунге-Кутта

2,0	1,000000	0,237814	0,283092	0,289428	0,343770
2,4	1,287770	0,343287	0,405555	0,414952	0,491064
2,8	1,700330	0,490319	0,578250	0,592296	0,700948
3,2	2,289057	0,699781	0,825797	0,846849	1,003755
3,6	3,130528

3. Строим графики приближенных решений (рис. 4.4).

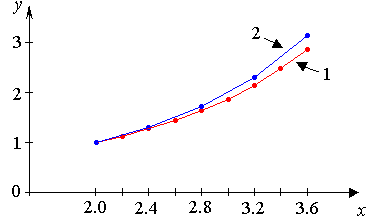
Рис. 4.4. Графики приближенных решений, полученных методом

Эйлера (кривая 1) и методом Рунге-Кутта (кривая 2)

4. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab4.mcd. Вводим функцию, стоящую в правой части уравнения (4.1), начальное условие, правую и левую границу интегрирования

5. С помощью заложенного в файле Lab4.mcd программного блока системы Mathcad (в начале любого блока обязательно должно присутствовать слово Given)

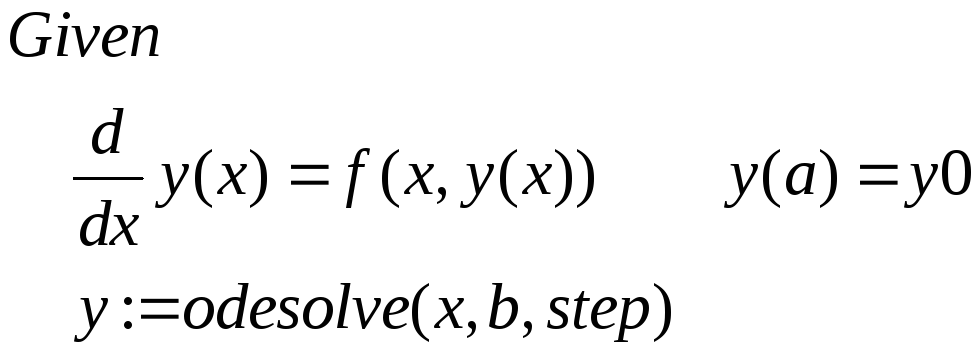
находим решение дифференциального уравнения с шагом интегрирования (в дальнейшем будем называть его точным решением). Выписываем полученные значения этого решения в промежуточных точках (табл. 4.4)

Таблица 4.4

Точное решение задачи Коши

2,0	1,0000000000
2,2	1,1307465872
2,4	1,2877847424
2,6	1,4757530270
2,8	1,7003752743
3,0	1,9686608656
3,2	2,2891619457
3,4	2,6722961416
3,6	3,1307469976

И по этим значениям строим график точного решения (рис. 4.5)

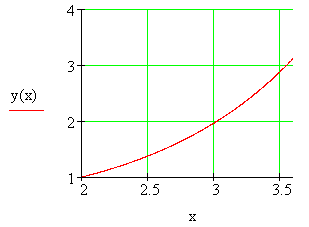
Рис. 4.5. График точного решения, полученного с помощью компьютера

6. Используя значения табл. 4.4, вычисляем локальные абсолютные погрешности, с которыми найдены приближенные решения по методу Эйлера и Рунге-Кутта (табл. 4.5).

Таблица 4.5

Таблица погрешностей решений задачи Коши методами Эйлера и Рунге-Кутта

	(точное решение)	(метод Эйлера)		(метод Рунге-Кутта)
2,0	1,0000000000	1,000	0,0000000	1,000000	0,0000000
2,2	1,1307466119	1,119	0,0117466
2,4	1,2877848040	1,260	0,0277847	1,287770	0,0000147
2,6	1,4757531434	1,428	0,0477530
2,8	1,7003754702	1,626	0,0743753	1,700330	0,0000453
3,0	1,9686611750	1,860	0,1086609
3,2	2,2891624149	2,135	0,1541619	2,289057	0,0001049
3,4	2,6722968333	2,460	0,2122961
3,6	3,1307479958	2,843	0,2877470	3,130528	0,0002190

Находим максимум величин и , определяем, что локальная погрешность решения методом Эйлера в точках , полученного с шагом , не превышает

,

а локальная погрешность решения методом Рунге-Кутта, полученного с шагом , не превышает

.

То есть даже небольшое количество точек разбиения отрезка интегрирования обеспечивает малую погрешность решения методом Рунге-Кутта.

7. Подставив , получим с помощью компьютера решение задачи Коши методом Рунге-Кутта и, используя уже найденное решение для , определим по формуле (4.7) относительную погрешность.

Таблица 4.6

Относительная погрешность решения методом Рунге-Кутта

2,0	1,000000	1,000000	0,000
2,2	1,130746
2,4	1,287784	1,287770	0,000014
2,6	1,475751
2,8	1,700372	1,700330	0,000042
3,0	1,968656
3,2	2,289155	2,289057	0,000098
3,4	2,672286
3,6	3,130733	3,130528	0,000205

Находим максимум величин , определяем, что относительная погрешность решения, полученного с шагом , не превышает

8. Все расчеты оформляются в виде отчета по лабораторной работе.