1.5. Вопросы для самоконтроля

Что называется решением системы линейных алгебраических уравнений?
Какая система линейных алгебраических уравнений совместна, какая несовместна?
Какая совместная система линейных алгебраических уравнений определена, какая неопределена?
Что называется основной и расширенной матрицей системы линейных уравнений?
Что такое ранг матрицы A?
Сформулируйте теорему Кронекера-Капелли.
Когда система линейных алгебраических уравнений определена и когда неопределена?
Что такое элементарные преобразования строк матрицы?
Опишите структуру бланка расчета в методе Гаусса.
Как выполняется контроль текущих вычислений при реализации метода Гаусса?
Для чего предназначен контрольный столбец и как он формируется?
Опишите алгоритм прямого хода метода Гаусса и запишите расчетные формулы прямого хода.
Опишите алгоритм обратного хода метода Гаусса и запишите расчетные формулы обратного хода.
В чем состоит смысл выбора ведущей строки в методе Гаусса?
Что называется невязками уравнений системы?

2. Решение нелинейных уравнений

2.1. Постановка задачи

Целью данной лабораторной работы является нахождение действительных корней уравнения

(2.1)

где – некоторая заданная функция. В некоторых частных случаях это уравнение может быть решено аналитически (например, линейное или квадратное уравнения). Однако при решении прикладных задач уравнение (2.1) обычно не может быть решено аналитически. В таких случаях используют приближенные методы решения: графический, метод половин-ного деления, метод касательных, метод хорд, комбинированный и другие.

Приближенное нахождение действительных корней уравнения (2.1) обычно складывается из двух этапов.

Отделение корней, т. е. отыскание для каждого корня такого отрезка [a, b], внутри которого лежит только этот корень и отсутствуют другие корни.
Уточнение приближенных корней, т. е. доведение их приближенных значений до заданной точности.

2.2. Отделение корней уравнения. Графический метод

Для первого этапа работы по отделению корней полезен графический метод решения уравнения (2.1). В этом случае строится график функции и находятся абсциссы точек пересечения графика с осью Ox (рис. 2.1). На рис. 2.1 и – корни уравнения (2.1).

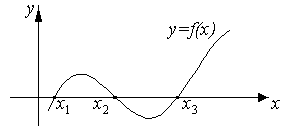
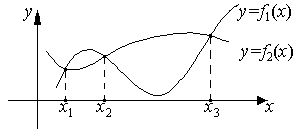
Рис. 2.1. Графическое решение Рис. 2.2. Графическое решение

уравнения (2.1) уравнения (2.2)

Если же исходное уравнение (2.1) может быть представлено в виде

(2.2)

то строятся графики функций и , и находят уже абсциссы их точек пересечения. На рис. 2.2 и – корни уравнения (2.2).

Графический метод достаточно прост для реализации на ЭВМ, но не достаточно эффективен, так как для уточнения корня каждый раз требуется строить график (или и ) во все более крупном масштабе.

Отрезок , внутри которого находится единственный корень уравнения (2.1), будем называть начальным.

Для нахождения начального отрезка следует использовать следующие теоремы [1]–[3].

Теорема 1. Если функция непрерывна на отрезке и на концах отрезка принимает значения разных знаков, т. е. , то между и найдется по крайней мере одна точка , в которой .