4.8. Вопросы для самоконтроля

1. Что называется обыкновенным дифференциальным уравнением? Записать в нормальной форме уравнение первого порядка.

2. Что является частным и общим решением дифференциального уравнения?

3. Как ставится задача Коши для дифференциального уравнения первого порядка? При каких условиях эта задача имеет, причем единственное, решение?

4. Каков геометрический смысл дифференциального уравнения первого порядка? Что означает решить задачу Коши с геометрической точки зрения?

5. В каком виде ищется решение задачи Коши численным методом?

6. Записать расчетную формулу метода Эйлера. Каков геометрический смысл метода Эйлера?

7. Записать расчетные формулы для метода Рунге-Кутта.

8. Записать формулы для расчета погрешности в методах Эйлера и Рунге-Кутта.

9. Привести алгоритм выбора начального шага в методе Рунге-Кутта.

5. Аппроксимация функции на основании экспериментальных данных по методу наименьших квадратов

5.1. Постановка задачи

Пусть проводится эксперимент, целью которого является исследование зависимости некоторой физической величины от физической величины (например, зависимости пути, пройденного телом, от времени и т. д.), или одним из численных методов получено решение дифференциального уравнения. В результате имеется значений функции при соответствующих значениях аргумента . Результаты записаны в табл. 5.1.

Таблица 5.1

Таблица результатов эксперимента

	1	2	…		…
			…		…
			…		…

Требуется установить функциональную зависимость величины от величины

(5.1)

Если построить график этой зависимости, то можно заметить, что экспериментальные точки обнаруживают некоторые отклонения от видимой общей закономерности (рис. 5.1). Эти отклонения связаны с неизбежными при всяком опыте ошибками измерения или погрешностями вычислений.

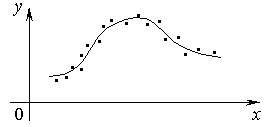
Рис. 5.1. Отклонение экспериментальных точек от

функциональной зависимости

Поэтому нужно так подобрать функцию , чтобы по возможности точно определить общую тенденцию зависимости от , но вместе с тем сгладить незакономерные, случайные уклонения, связанные с названными выше ошибками.

Для решения этой задачи обычно применяют расчетный метод, известный под названием «метода наименьших квадратов». Этот метод дает возможность при заданном типе зависимости так выбрать ее числовые параметры, чтобы кривая в известном смысле наилучшим образом отображала экспериментальные данные.

5.2. Выбор типа кривой

Тип кривой может быть выбран из различных соображений. Часто этот вопрос решается непосредственно по внешнему виду экспериментальной зависимости. Пусть, например, экспериментальные точки расположены на координатной плоскости так, как изображено на рис. 5.2.

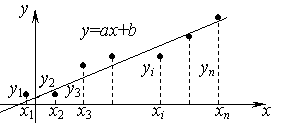
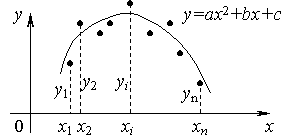
Рис. 5.2. Линейная зависимость Рис. 5.3. Квадратичная зависимость

Естественно предположить, что это линейная зависимость вида . Зависимость, изображенная на рис. 5.3, хорошо может быть представлена многочленом второй стерени .

Если речь идет о периодической функции, то можно выбрать для ее изображения несколько гармоник тригонометрического ряда и т. д.

Очень часто вид зависимости (линейная, квадратичная, показательная и т. д.) бывает известен из физических соображений, связанных с существом решаемой задачи, а из опыта требуется установить только значения параметров этой зависимости, причем выбрать их так, чтобы кривая в каком-то смысле наилучшим образом изображала зависимость, полученную в эксперименте.