1. Решение систем линейных уравнений методом гаусса

1.1. Постановка задачи

Пусть задана система n линейных алгебраических уравнений (СЛАУ) с n неизвестными :

(1.1)

или в матричной форме: , где

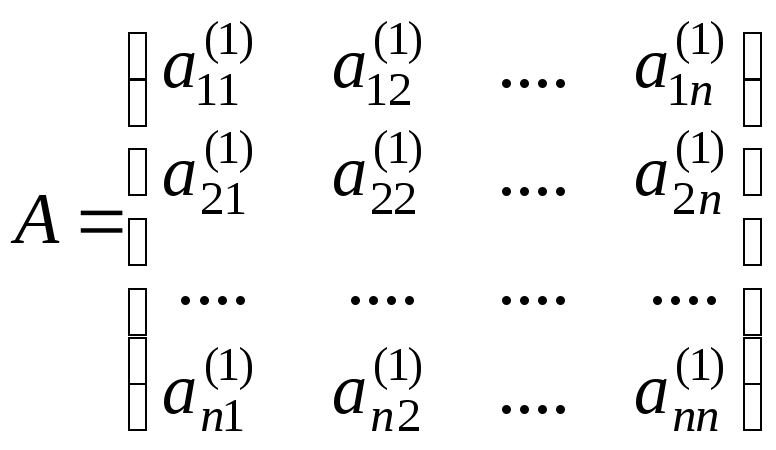– основная матрица системы, – столбец свободных элементов, 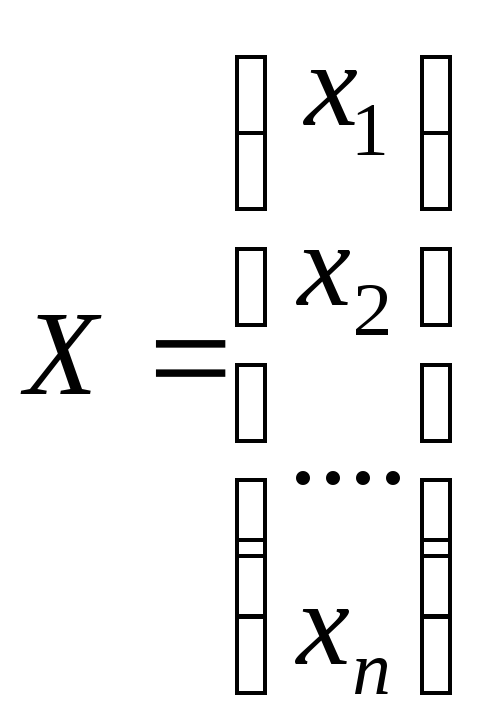– столбец неизвестных.

Решением системы (1.1) называется последовательность значений неизвестных , удовлетворяющая одновременно каждому уравнению из системы (1.1). Система решена полностью, если все решения найдены.

Теорема Кронекера-Капелли: Для того чтобы система (1.1) была совместна (имела хотя бы одно решение), необходимо и достаточно, чтобы ранг основной матрицы A и ранг расширенной матрицы системы (основная матрица системы с добавлением справа столбца свободных элементов)

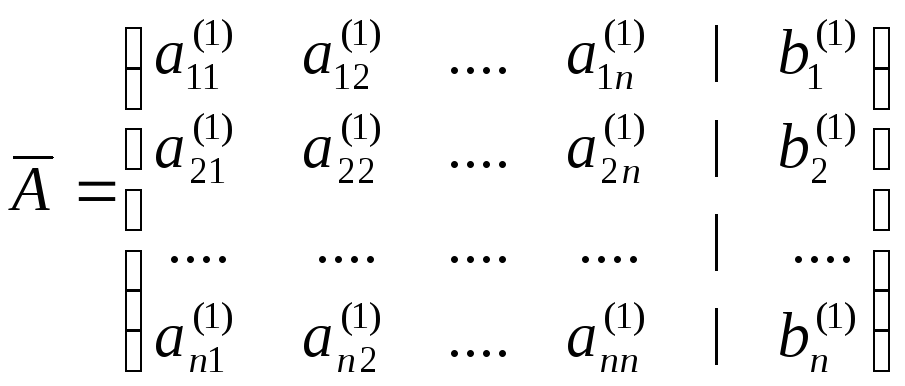(1.2)

были равны .

При этом, если ранг равен числу неизвестных , то система (1.1) имеет единственное решение, т. е. определена. Если , то система (1.1) имеет бесконечное множество решений, зависящих от (n–r) произвольных параметров, т. е. неопределена.

Существует много методов решения таких систем [1]–[3]. В данной лабораторной работе будем решать ее методом Гаусса с частичным выбором ведущего элемента. Суть этого метода состоит в последовательном исключении неизвестной из 2, 3,…, n-го уравнений, – из 3, 4,…, n-го уравнений и т. д. Для этого на каждом шаге преобразования сначала выбираем так называемое «ведущее уравнение». На i-м шаге (т. е. при исключении неизвестного , i=1, 2,…, n–1) в качестве ведущего уравнения нужно взять то, из i-го, (i+1)-го,…, n-го уравнений, в котором коэффициент перед имеет наибольшую абсолютную величину. Ведущее уравнение ставим на место i-го уравнения, и во всех ниже расположенных уравнениях с помощью ведущего уравнения исключаем . После n–1 шага таких преобразований исходная система (1.1) будет приведена к следующему виду:

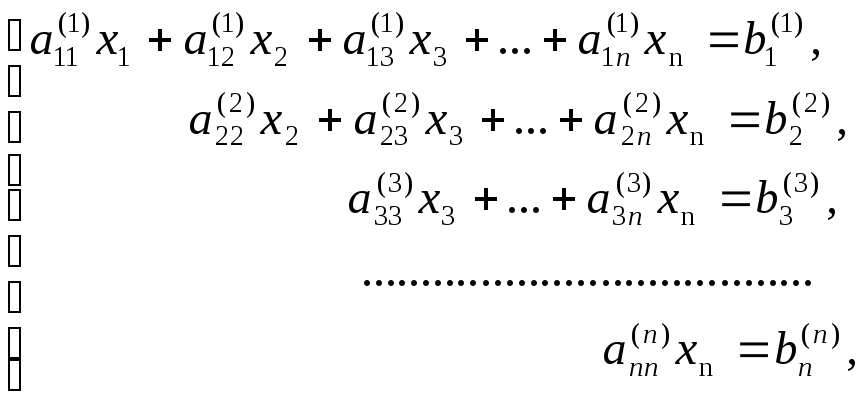(1.3)

с треугольной расширенной матрицей системы

.

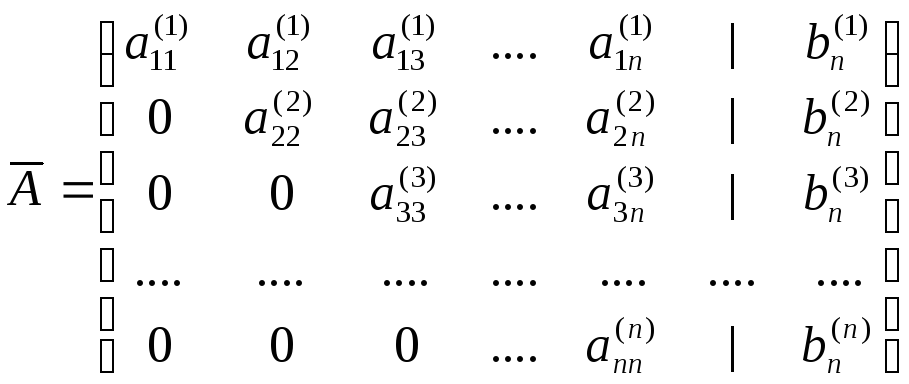Исключение одного неизвестного (k = 1, 2,…, n) вышеуказанным способом называется циклом процесса. Выполнение всех циклов, в результате которых получается система (1.3), называется прямым ходом метода Гаусса.

Запишем расчетные формулы процесса исключения неизвестного на k-м цикле. Пусть уже исключены , т. е. получены элементы, равные 0 ниже главной диагонали в первых (k–1)-м столбцах расширенной матрицы системы . Тогда остались такие уравнения с отличными от нуля элементами ниже главной диагонали:

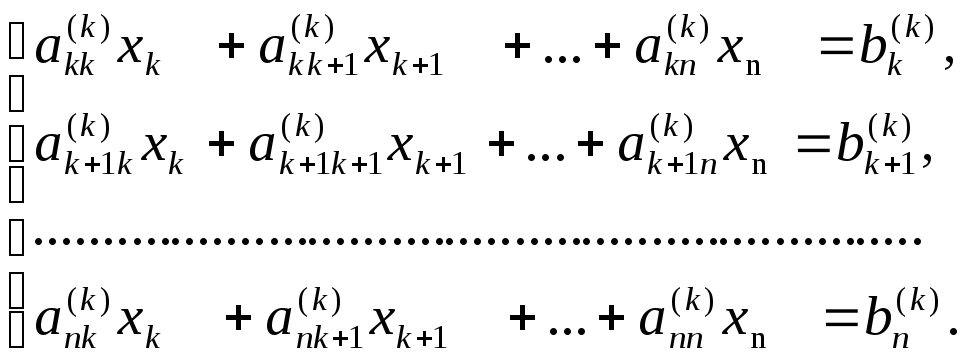(1.4)

Для исключения неизвестной переставим уравнения подсистемы (1.4) так, чтобы верхнее уравнение имело самый большой по модулю коэффициент перед , т. е. выберем ведущее уравнение. Это необходимо для уменьшения вычислительной погрешности.

Пусть – коэффициент с наибольшей абсолютной величиной среди коэффициентов, стоящих перед неизвестной во всех уравнениях системы (1.4). С помощью первого уравнения системы (1.4) исключим неизвестное из остальных уравнений. Для этого k-ое уравнение умножим на число 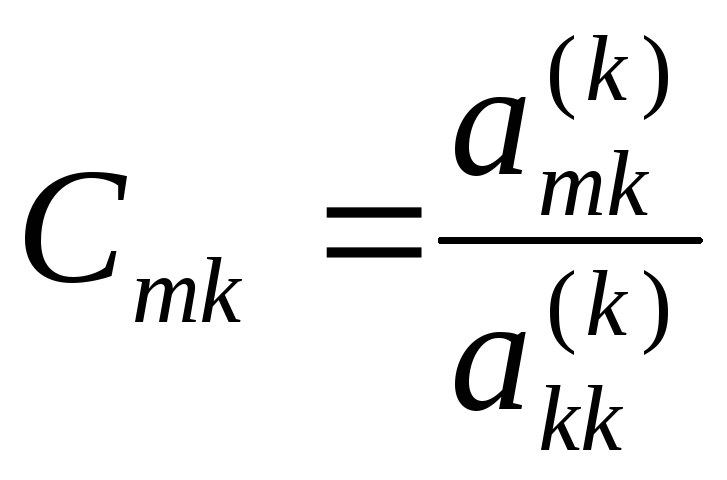и вычтем из m-го уравнения (m=k+1,…, n). Тогда коэффициент при m-го уравнения обратится в 0, а остальные получатся по следующим формулам:

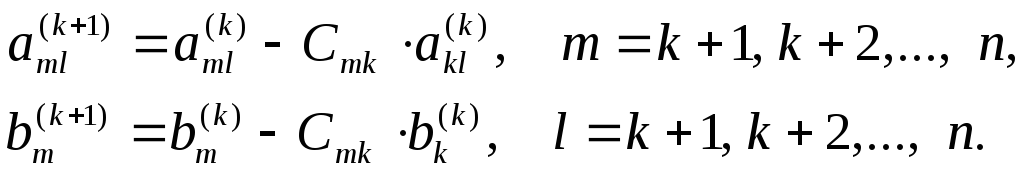(1.6)

Вычисления выполняются последовательно для всех указанных индексов. После их окончания окажется исключенным из k+1, k+2,…, n-го уравнений. На этом очередной цикл исключения заканчивается. Процесс продолжается дальше аналогично до завершения прямого хода.

В результате выполнения прямого хода метода Гаусса в случае определенной системы в последнем уравнении системы (1.3) остается одно неизвестное , в предпоследнем – два: и и т. д. Это позволяет из последнего уравнения найти , затем, подставив его в предпоследнее, найти и т. д. Этот этап задачи, состоящий в нахождении из преобра-зованной системы (1.3), получил название обратного хода метода Гаусса.

Замечание 1. Метод Гаусса относится к точным методам решения рассматриваемых систем. Это значит, что при выполнении всех операций без округлений, получится точное решение системы. Так как на практике все вычисления ведутся обычно с округлением, то значения неизвестных неизбежно будут содержать погрешности. Если матрица системы хорошо обусловлена (матрица A плохо обусловлена, если малые изменения ее элементов приводят к существенным изменениям элементов обратной матрицы ), то оценить погрешность решения можно с помощью вычисления невязок, представляющих собой модули разностей между правыми и левыми частями уравнений системы (1.1):

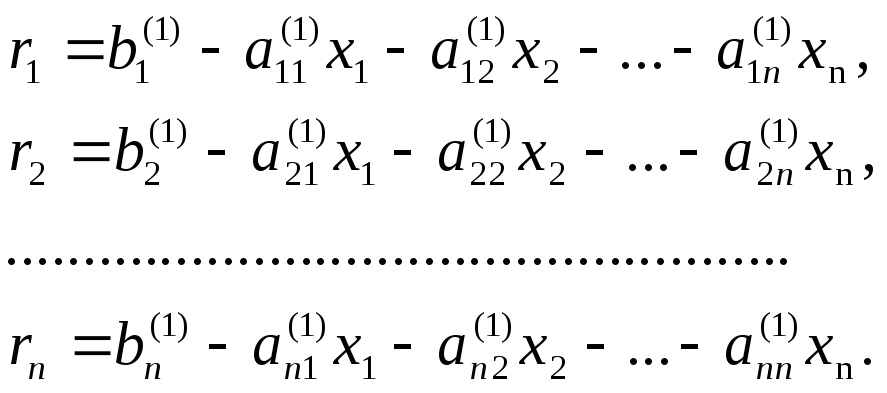
Если невязки малы по модулю, то решение системы найдено достаточно точно.

Замечание 2. Технически решение системы (1.1) методом Гаусса удобнее вести, применяя к расширенной матрице системы элементарные преобразования строк:

1) перестановка двух строк местами;

2) умножение строки на действительное число, отличное от нуля;

3) сложение двух строк.

Применяя конечное число этих преобразований, получим расширенную матрицу эквивалентной системы, имеющей то же самое решение. При этом этапы выполнения прямого хода обычно оформляются в виде специального расчетного бланка, как это будет показано в примере (табл. 1.2). Для контроля правильности выполнения текущих вычислений в бланк вводится дополнительный столбец, обозначенный . На начальном этапе заполнения бланка первые элементы этого столбца получаются суммированием других элементов строк матрицы . Остальные элементы контрольного столбца вычисляются аналогично другим элементам по формулам (1.6) в каждом цикле. Если в текущем цикле все вычисления были выполнены правильно, то сумма элементов каждой строки (кроме последнего) должна быть равна последнему элементу . Возможно расхождение между суммой и элементом в последнем знаке из-за ошибок округления.