5.3. Метод наименьших квадратов

Общепринятым методом решения данной задачи является метод наименьших квадратов, при котором требование наилучшего согласования кривой и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой по оси Oy была наименьшей.

Этот метод имеет перед другими методами сглаживания следующие преимущества:

а) он приводит к сравнительно простому математическому способу определения параметров ;

б) допускает достаточно веское теоретическое обоснование с вероятностной точки зрения [4].

Перейдем к задаче определения параметров , исходя из метода наименьших квадратов. Пусть имеется таблица экспериментальных данных (табл. 5.1), и пусть из каких-то соображений выбран общий вид функции , зависящий не только от аргумента , но и от нескольких числовых параметров

Эти параметры и требуется выбрать согласно методу наименьших квадратов так, чтобы сумма квадратов отклонений от была наименьшей. Рассмотрим сумму квадратов разностей значений , полученных из эксперимента и функции , в соответствующих точках

(5.2)

Требуется выбрать параметры так, чтобы эта сумма была минимальной.

Из необходимого условия экстремума функции нескольких переменных следует, что эти значения удовлетворяют системе уравнений

(5.3)

или в развернутом виде

(5.4)

Эта система уравнений называется нормальной системой метода наименьших квадратов. Она содержит столько же уравнений, сколько неизвестных Решить систему (5.4) в общем виде нельзя, для каждого конкретного вида функции исследуется вопрос о существовании решения системы уравнений (5.4) и о существовании минимума функции

В частности, когда функция представлена линейной комбинацией функций

,

то нормальная система примет вид

()

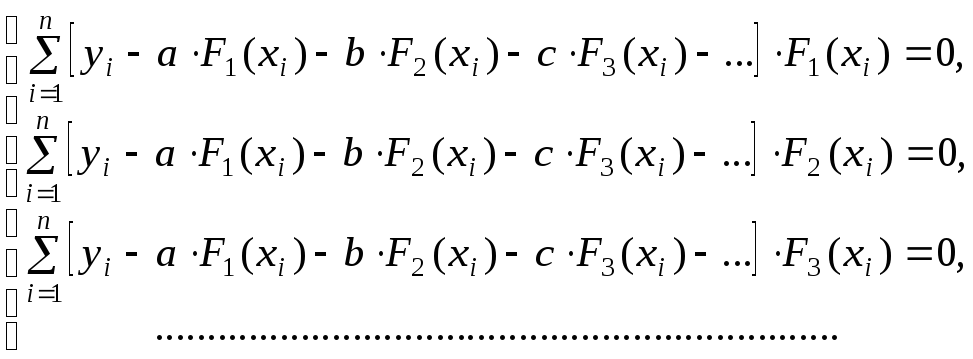5.4. Подбор параметров линейной функции методом наименьших квадратов

В эксперименте зарегистрирована совокупность значений (рис. 5.2). Требуется подобрать по методу наименьших квадратов параметры линейной функции , изображающей данную экспериментальную зависимость.

Имеем

(5.5)

Из формулы (5.2) следует, что в этом случае имеет вид

(5.6)

Это функция двух переменных и ( и – заданные числа). Следовательно,

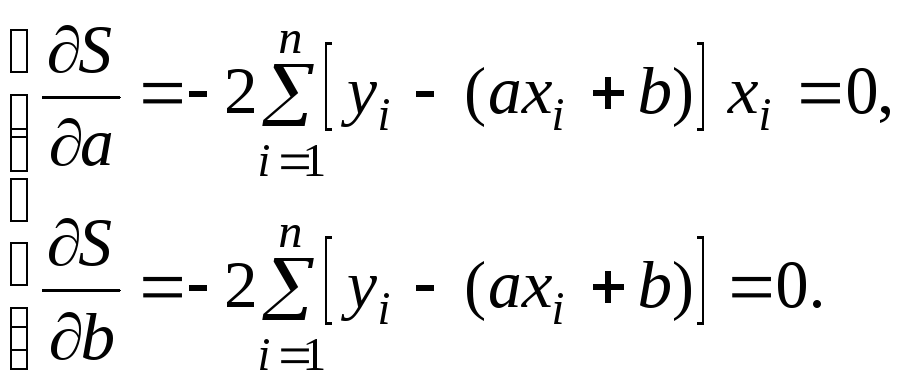
После преобразований нормальная система уравнений (5.4) принимает вид

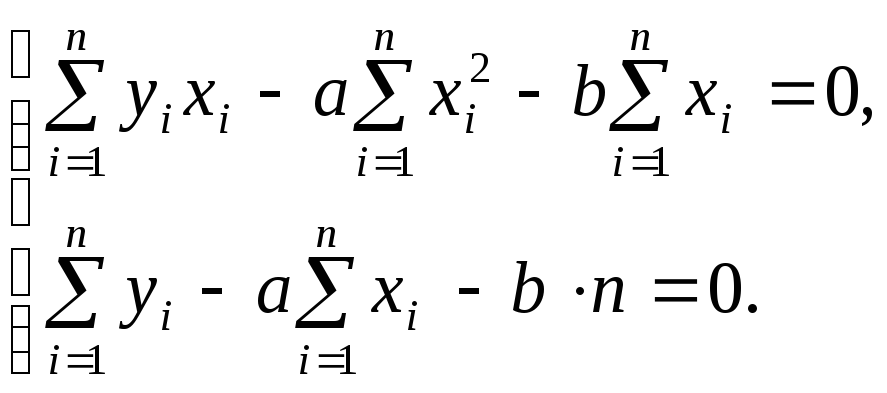(5.7)

Получили систему двух линейных уравнений с двумя неизвестными и .

Легко проверить, что система имеет решение и что при найденных значениях и функция имеет минимум.

На основании достаточных условий экстремума функции нескольких переменных находим

Поэтому

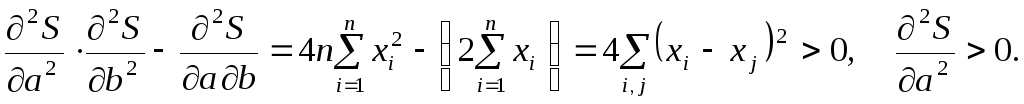
Следовательно, имеет минимум.

5.5. Подбор параметров квадратичной функции методом наименьших квадратов

В эксперименте зарегистрированы значения (рис. 5.3). Требуется методом наименьших квадратов подобрать параметры параболы , соответствующей данной эксперимен-тальной зависимости. Имеем

В этом случае выражение (5.2) имеет вид

(5.8)

Это функция трех переменных . Система уравнений (5.4) принимает вид

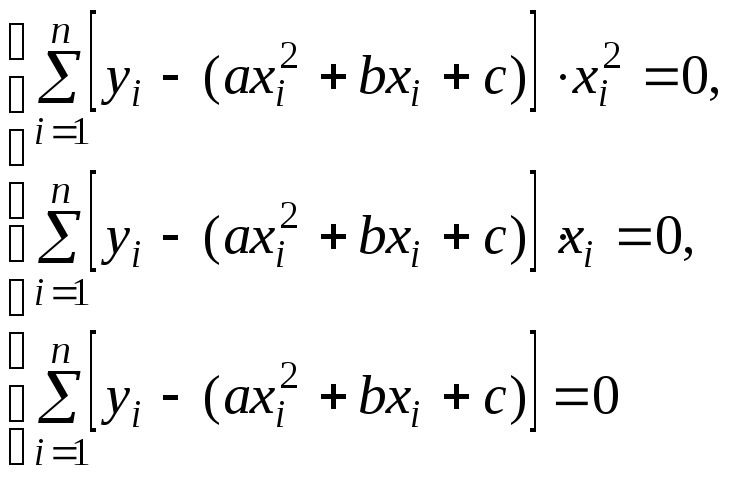
или в развернутом виде

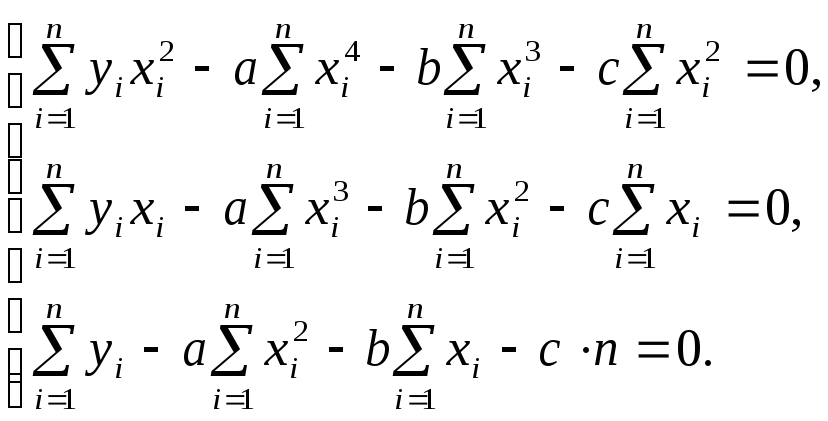(5.9)

Получили систему линейных уравнений для определения неизвестных . Можно показать, что система имеет единственное решение, и что при полученных функция имеет минимум [3].