
- •Лабораторные работы по высшей математике
- •432027, Ульяновск, ул. Северный Венец, 32
- •Оглавление
- •4.1. Постановка задачи ……………………………………………… 39
- •Инструкция по технике безопасности
- •Введение
- •Пакет программ лабораторных работ
- •1. Решение систем линейных уравнений методом гаусса
- •1.1. Постановка задачи
- •1.2. Задание на лабораторную работу
- •1.3. Порядок выполнения работы в компьютерном классе
- •1.4. Пример выполнения работы
- •1.5. Вопросы для самоконтроля
- •2. Решение нелинейных уравнений
- •2.1. Постановка задачи
- •2.2. Отделение корней уравнения. Графический метод
- •2.3. Метод половинного деления
- •2.4. Метод Ньютона
- •2.5. Метод хорд
- •2.6. Комбинированный метод
- •2.7. Задание на лабораторную работу
- •2.8. Порядок выполнения работы в компьютерном классе
- •2.9. Пример выполнения работы
- •2.9. Вопросы для самоконтроля
- •3. Вычисление определенных интегралов
- •3.1. Постановка задачи
- •3.2. Методы прямоугольников и трапеций
- •3.3. Метод Симпсона
- •3.4. Оценка погрешностей методов
- •3.5. Задание на лабораторную работу
- •3.7. Порядок выполнения работы в компьютерном классе
- •3.6. Пример выполнения работы
- •3.8. Вопросы для самоконтроля
- •4. Численное интегрирование обыкновенных дифференциальных уравнений первого порядка
- •4.1. Постановка задачи
- •4.2. Метод Эйлера
- •4.3. Метод Рунге-Кутта
- •4.4. Выбор шага интегрирования
- •4.5. Задание на лабораторную работу
- •4.6. Порядок выполнения работы в компьютерном классе
- •4.7. Пример выполнения работы
- •4.8. Вопросы для самоконтроля
- •5. Аппроксимация функции на основании экспериментальных данных по методу наименьших квадратов
- •5.1. Постановка задачи
- •5.2. Выбор типа кривой
- •5.3. Метод наименьших квадратов
- •5.4. Подбор параметров линейной функции методом наименьших квадратов
- •5.5. Подбор параметров квадратичной функции методом наименьших квадратов
- •5.6. Задание на лабораторную работу
- •5.7. Порядок выполнения работы в компьютерном классе
- •5.8. Пример выполнения работы
- •5.9. Вопросы для самоконтроля
- •6. Прикладной математический пакет «mathcad»
- •6.1. О программе
- •6.2. Основные понятия и функции
- •6.3. Операторы математического анализа
- •6.4. Функции и операторы матриц
- •6.5. Создание декартовых графиков на плоскости
- •6.6. Программные блоки
- •Библиографический список
4.2. Метод Эйлера
Метод
Эйлера состоит в следующем. Отрезок
![]() ,
на котором ищется приближенное решение,
делится точками
,
на котором ищется приближенное решение,
делится точками
![]()
на n
равных частей, где
![]() – шаг интегрирования дифференциального
уравнения. Зная значение
– шаг интегрирования дифференциального
уравнения. Зная значение
![]() решения
решения
![]() в точке
в точке
![]() ,
можно найти приближенно
,
можно найти приближенно
![]() в точках
в точках
![]() по следующей рекуррентной формуле:
по следующей рекуррентной формуле:
![]() (4.3)
(4.3)
Геометрически
в методе Эйлера искомую интегральную
кривую на интервале
![]() заменяем отрезком касательной к этой
интегральной кривой в точке
заменяем отрезком касательной к этой
интегральной кривой в точке
![]() (рис. 4.2). Уравнение касательной имеет
вид
(рис. 4.2). Уравнение касательной имеет
вид
![]()
где
![]() .
Поэтому ордината касательной в точке
.
Поэтому ордината касательной в точке
![]() равна
равна
![]() ,
т. е. получили формулу (4.3) для случая
,
т. е. получили формулу (4.3) для случая
![]() .
Далее строим касательную в точке
.
Далее строим касательную в точке
![]() к интегральной кривой 2, которая уже не
совпадает с искомой. Находим ординату
к интегральной кривой 2, которая уже не
совпадает с искомой. Находим ординату
![]() касательной в точке
касательной в точке
![]() ,
получаем формулу (4.3) уже при
,
получаем формулу (4.3) уже при
![]() .
И так до тех пор, пока не достигнем конца
отрезка b (рис. 4.3).
.
И так до тех пор, пока не достигнем конца
отрезка b (рис. 4.3).
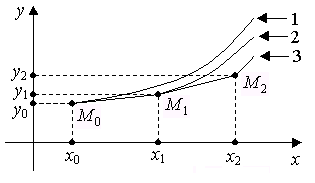
Рис. 4.2. Графическая иллюстрация метода Эйлера
1 – искомая интегральная кривая, 2,3 – другие интегральные кривые

Рис. 4.3. Графическая иллюстрация метода Эйлера
1 – ломаная Эйлера, 2 – искомая интегральная кривая
Для
оценки локальной погрешности метода
Эйлера в точке
![]() используется неравенство [1]–[3]
используется неравенство [1]–[3]
![]() (4.4)
(4.4)
где
![]() – точное значение решения задачи Коши
в точке
– точное значение решения задачи Коши
в точке
![]() ,
а
,
а
![]() – приближенные значения решения,
вычисленные по формуле (4.3) с шагами
– приближенные значения решения,
вычисленные по формуле (4.3) с шагами
![]() и
и
![]() соответственно. Из неравенства (4.4)
следует, что для достижения необходимой
точности
соответственно. Из неравенства (4.4)
следует, что для достижения необходимой
точности
![]() нужно просчитать значение
нужно просчитать значение
![]() по формуле (4.3) с шагом
по формуле (4.3) с шагом
![]() ,
а затем, уменьшив шаг вдвое, снова
повторить расчеты. Если при этом окажется,
что для всех
,
а затем, уменьшив шаг вдвое, снова
повторить расчеты. Если при этом окажется,
что для всех
![]() выполняется неравенство:
выполняется неравенство:
![]() то на шаге
то на шаге
![]() достигнута необходимая точность.
достигнута необходимая точность.
4.3. Метод Рунге-Кутта
Метод Эйлера прост в реализации, но обладает сравнительно небольшой точностью. Поэтому для решения задачи Коши с повышенной точностью обычно используют метод Рунге-Кутта [1]–[3].
Как и
прежде, разбиваем отрезок интегрирования
![]() на n равных частей.
Зная значения
на n равных частей.
Зная значения
![]() – решение задачи Коши в точке
– решение задачи Коши в точке
![]() ,
будем искать значение решения в точке
,
будем искать значение решения в точке
![]() по следующей формуле Рунге-Кутта:
по следующей формуле Рунге-Кутта:
![]() (4.5)
(4.5)
где
 (4.6)
(4.6)
Вычисления
по формулам (4.5), (4.6) выполняются в
следующем порядке. Для начальной точки
![]() ,
где
,
где
![]() ,
вычисляют
,
вычисляют
![]() ,
затем последовательно
,
затем последовательно
![]() и
и
![]() .
После этого все значения подставляются
в формулу (4.5)
.
После этого все значения подставляются
в формулу (4.5)
![]() и находится
и находится
![]() при
при
![]() .
Далее процесс продолжается аналогично
до конца отрезка
.
Далее процесс продолжается аналогично
до конца отрезка
![]() .
.
Для оценки локальной погрешности метода Рунге-Кутта используется уже неравенство [2], [3]:
![]() (4.7)
(4.7)
где
![]() имеют тот же смысл, что и в неравенстве
(4.4).
имеют тот же смысл, что и в неравенстве
(4.4).
4.4. Выбор шага интегрирования
Точность
методов Эйлера и Рунге-Кутта существенно
зависит от величины шага интегрирования
h. Можно доказать [2],
[3], что погрешность метода Эйлера имеет
порядок h, а метода
Рунге-Кутта – порядок
![]() .
Т. е. для достижения одной и той же
точности в методе Эйлера нужно выбрать
гораздо меньший шаг интегрирования,
чем в методе Рунге-Кутта.
.
Т. е. для достижения одной и той же
точности в методе Эйлера нужно выбрать
гораздо меньший шаг интегрирования,
чем в методе Рунге-Кутта.
Рассмотрим
подробнее процедуру выбора и уточнения
шага интегрирования на примере метода
Рунге-Кутта. Пусть
![]() – заданная точность решения задачи
Коши. Поскольку
– заданная точность решения задачи
Коши. Поскольку
![]() (где c=const),
то начальное значение
(где c=const),
то начальное значение
![]() можно выбрать из неравенства
можно выбрать из неравенства
![]() (4.8)
(4.8)
При этом, чтобы попасть после n шагов интегрирования из точки a в точку b, необходимо одновременное выполнение условия:
![]() (целое число).
(4.9)
(целое число).
(4.9)
Кроме
того, для подсчета погрешности метода
Рунге-Кутта по формуле (4.7), нужно будет
сделать просчет по формулам (4.5), (4.6) с
шагом 2h. Поэтому
необходимо также, чтобы отношение
![]() было четным.
было четным.
После
выбора начального значения шага
![]() проводится его уточнение. Для этого из
точки
проводится его уточнение. Для этого из
точки
![]() просчет по формулам (4.5), (4.6) выполняется
дважды сначала с шагом h,
а затем из той же точки с шагом 2h.
При этом получаются два значения решения
задачи (
просчет по формулам (4.5), (4.6) выполняется
дважды сначала с шагом h,
а затем из той же точки с шагом 2h.
При этом получаются два значения решения
задачи (![]() и
и
![]() )
в одной и той же точке
)
в одной и той же точке
![]() .
Если
.
Если
![]() ,
то
,
то
![]() можно выбрать в качестве шага
интегрирования, иначе необходимо
уменьшить h в два раза
и повторить процедуру проверки.
можно выбрать в качестве шага
интегрирования, иначе необходимо
уменьшить h в два раза
и повторить процедуру проверки.
