1.5. Прямая
1°. Общие уравнения прямой в пространстве.
Прямую в пространстве можно однозначно определить пересечением двух плоскостей
(1.29)
нормальные векторы
и
которых непараллельны. Уравнения (1.29)
называются общими уравнениями
прямой в пространстве.
2°. Канонические уравнения прямой.
Пусть
– вектор,
параллельный прямой
,
называемый направляющим вектором
этой прямой, и
– точка, лежащая на этой прямой. Вектор
соединяющий точку
с произвольной точкой
прямой
,
параллелен вектору
Поэтому координаты вектора
и вектора
пропорциональны:
.
(1.30)
Уравнения (1.30) называются каноническими
уравнениями прямой в пространстве
и определяют прямую, проходящую через
точку
и параллельную вектору
.
3°. Параметрические уравнения прямой.
От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям:
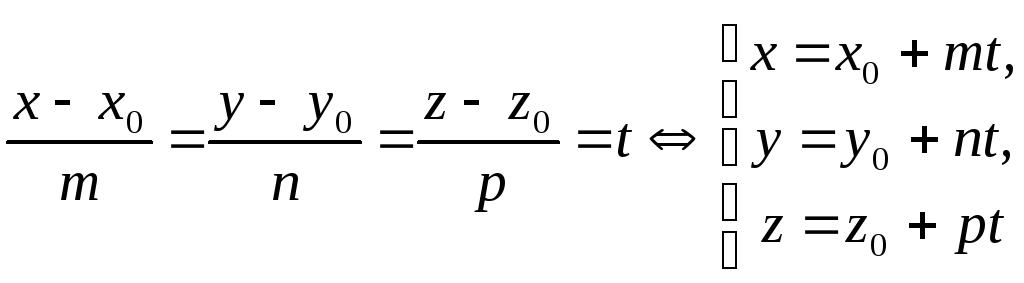(1.31)
или в векторной форме
;
(1.32)
где
и
– радиус-векторы точек
и
,
– направляющий вектор прямой,
– параметр.
4º. Уравнение прямой, проходящей через две точки.
Если прямая
проходит через две заданные точки
и
,
то в качестве направляющего вектора
можно взять вектор
.
Т. к. прямая проходит через точку
,
то, согласно уравнениям (1.30), уравнения
имеют вид
.
(1.33)
Уравнения (1.33) называются уравнениями прямой, проходящей через две данные точки.
5°. Угол между прямыми.
Пусть прямые
и
заданы уравнениями
и
.
Под углом между прямыми понимают
угол между направляющими векторами
и
.
Величина угла
между ними определяется из формулы
.
(1.34)
Для нахождения острого угла между
прямыми
и
числитель правой части формулы (1.34)
следует взять по модулю.
6°. Условие перпендикулярности двух прямых.
Если прямые
и
перпендикулярны, то скалярное произведение
их направляющих векторов
,
т. е.
.
(1.35)
7°. Условие параллельности двух прямых.
Если прямые
и
параллельны, то параллельны их направляющие
векторы
и
.
Следовательно, координаты этих векторов
пропорциональны:
.
(1.36)
8°. Условие компланарности двух прямых.
Пусть прямая
проходит через точку
,
прямая
– через точку
.
Прямые
и
лежат в одной плоскости, если векторы
,
и
компланарны. Условием компланарности
векторов является равенство нулю их
смешанного произведения. Следовательно,
необходимым и достаточным условием
нахождения двух прямых, заданных их
каноническими уравнениями, в одной
плоскости является
.
(1.37)
При выполнении условия (1.37) прямые
и
либо пересекаются, если
либо параллельны, если
Если условие (1.37) не выполняется, то
прямые
и
являются скрещивающимися.
9°. Расстояние от точки до прямой в пространстве.
Расстояние от точки
до прямой (1.30), проходящей через точку
в направлении вектора
,
вычисляется по формуле
.
(1.38)
10°. Угол между прямой и плоскостью.
Углом между прямой
и плоскостью Р называют угол
,
образованный прямой
и ее проекцией на плоскость Р.
Если прямая
задана каноническими уравнениями
(1.30), а плоскость Р – общим уравнением
,
тогда косинус угла между нормальным
вектором
к плоскости и направляющим вектором
прямой определяется
,
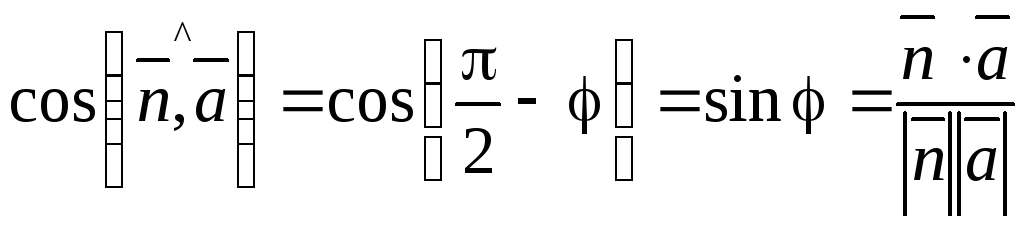и т. к.
для
,
получаем
.
(1.39)
Если прямая
параллельна плоскости Р, то векторы
и
перпендикулярны, а потому
,
т. е.
(1.40)
является условием параллельности прямой и плоскости.
Если прямая
перпендикулярна плоскости Р, то
векторы
и
параллельны. Поэтому равенства
(1.41)
являются условиями перпендикулярности прямой и плоскости.
11°. Пересечение прямой с плоскостью.
Для определения точки пересечения
прямой с плоскостью нужно решить
совместно их уравнения, для чего следует
воспользоваться параметрическими
уравнениями прямой (1.31). Подставляя
из этих уравнений в уравнение плоскости
,
получим уравнение относительно
неизвестного параметра t:
.
(1.42)
Возможны следующие случаи:
1) При
уравнение (1.42) имеет единственное решение
.
Подставив это значение t в параметрическое уравнение прямой, найдем координаты точки пересечения М.
2) При
,
(1.43)
уравнение (1.42) не имеет решения, и прямая не имеет общих точек с плоскостью. Условия (1.43) являются условиями параллельности прямой и плоскости.
3) При
,
(1.44)
любое значение t является решением уравнения (1.42), т. е. любая точка прямой принадлежит плоскости. Равенства (1.44) называются условиями принадлежности прямой плоскости.